Курсовая работа студента кафедры динамической геологии геологического факультета МГУ

---

Олесь Савчук

СИНЕРГЕТИКА ГЕОЛОГИЧЕCКИХ СИСТЕМ

Введение

Термин «синергетика» предложен в 70-х годах немецким физиком Г. Хакеном. Его работы по синергетике были посвящены теории самоорганизации в различных природных системах. Слово «синергетика» происходит от греческого «Synergeia» - совместное действие, сотрудничество. В работах по синергетике излагаются общие подходы к изучению универсальных свойств явлений самоорганизации в динамических неравновесных системах. Особое значение при этом придается изучению роли коллективных, кооперативных эффектов в процессах самоорганизации.

Появление этого направления подготовлено широким кругом физиков, химиков, математиков, специалистов других областей. Основополагающее значение имели работы русского ученого, работавшего в Бельгии, И.Р. Пригожина.

Лауреат Нобелевской премии физик-теоретик Швингер в 1962 г. ввел понятие о трех уровнях в науке: первый – события, явления, факты; второй – законы, которым подчинены эти события, явления и факты; третий – инварианты или законы законов. В этом плане синергетика может быть отнесена к разряду инвариантов.

На базе учения об открытых системах, обменивающихся с внешней средой веществом и энергией, развивалась неравновесная термодинамика, итоговым результатом которой на сегодняшний день является теория диссипативных структур, разработанная И.Р. Пригожиным. Диссипативные структуры – пространственные или пространственно-временные структуры, которые могут возникать вдали от равновесия в нелинейной области, когда параметры системы превышают критические значения.

Любые системы, полная энергия которых при движении убывает, переходя в другие формы (например, механическая энергия в теплоту) (при этом образуются различные диссипативные структуры, способствующие этому процессу), получили название диссипативных систем. Практически все геологические системы диссипативны.

При изучении переходов неравновесных систем в новые состояния подвижного равновесия (стационарные состояния) обнаружилось развитие колебательных процессов. Сформировалось особое направление – теория автоколебаний, разработанная А.А. Андроновым.

Значительным достижением математики стало введенное Б. Мандельбротом понятия фрактала для обозначения нерегулярных, но самоподобных фигур. Фрактальная геометрия описывает чрезвычайно большое количество природных объектов и становится мощным средством в руках исследователя для поиска общих закономерностей в сложных природных процессах.

Невероятные результаты были получены учеными при исследовании различных хаотических систем. Был обнаружен некий порядок, выдающий себя за хаос – это огромное достижение нелинейной динамики.

Также была разработана теория самоорганизованной критичности, позволяющая на качественно новом уровне объяснять «катастрофические» природные процессы. Моделируя эти процессы, были получены фрактальные аналоги реальных природных объектов. И эти процессы описываются степенными законами с дробными показателями.

Все новейшие достижения нелинейной науки включает в себя междисциплинарное направление – синергетика. В её основе лежит концепция параметров порядка, которые определяют полностью поведение системы, т.к. по принципу Хакена все элементы подчинены данным параметрам. Знание этих параметров позволяет выделить в явлении главное и описывать сложные системы просто.

В геологии мы имеем дело с минеральным миром, где всё взаимосвязано, с миром неустойчивости и необратимости, нелинейности и обратных связей, эволюции и катастроф, хаоса и сложнейших структур, диссипации и самоорганизации. Короче говоря, нас окружает мир, далёкий от равновесия. Поэтому очень перспективна интеграция идей синергетики в геологию в самом широком плане.

Цель данной работы: на основании анализа литературы рассмотреть конкретные геологические объекты и процессы с точки зрения базовых понятий синергетики, объединяющей системный анализ, теорию диссипативных структур, теорию автоколебаний, нелинейную динамику, фрактальную геометрию, теорию самоорганизованной критичности.

Глава I. Вселенная как единая динамическая система, или от Аристотеля к Теории Хаоса

Хаос – более высокая форма порядка, где

случайность и бессистемные импульсы

становятся организующим принципом.

Б. Вильямс

Наша логика зародилась приблизительно 2500 лет назад, когда между двумя противоположными лагерями, представленными, с одной стороны, Аристотелем, а с другой — Гераклитом, велись философские войны. Аристотель верил в редукционистский подход: если разбить что-либо на мельчайшие составные части, можно понять, как это работает. Свойства системы являются непосредственным следствием свойств отдельных элементов. Его мнение: «Для решения проблем следует выбирать расчленения и деления». Аристотель поддерживал идею о том, что все имеет свои собственные границы, все может быть локализовано и категорировано. Аристотель – основоположник формальной логики и учения о логической дедукции.

Иной точки зрения придерживался оппонент философии Аристотеля Гераклит. Он интуитивно чувствовал, что Вселенная находится в постоянном движении, что стабильность и гомеостазис не являются нормой. Целое, разобранное на детали, в процессе синтеза снова собрать без потерь не удаётся. Его принцип рассмотрения от целого к частям, или поведения частей с позиций целого, был противоположным взглядам Аристотеля. Вероятно самое известное его изречение: «Всё течёт… Нельзя войти в одну и ту же реку однажды».

Нелинейный мир

Буквально до ХХ века классическая наука базировалась на предположении Аристотеля о том, что Вселенная аналогична точно идущим часам. «Естественное» положение вещей передавалось гладкими линиями, округлыми кривыми и формами. Непредвиденные отклонения в экспериментах рассматривались как «случайное поведение» и считались несущественными.

Для объяснения природных явлений пользовались «линейным» редукционистским подходом (в математике – сведение к интегралам). Так, Галилей писал: «Книга природы раскрыта перед нами, но она написана не теми буквами, из которых состоит наш алфавит: ее буквы — это треугольники, круги, шары», хотя в природе нельзя встретить ни одного листочка треугольной формы, облака в виде окружности или человека в форме шара.

На протяжении человеческой истории крупнейшие учёные с мировыми именами самым тщательным образом изучали законы мироздания и, проверив их действие экспериментально, формулировали эти законы. Однако не всё можно было проверить опытом, и не всё можно было объяснить (процесс познания вечен).

Поколения физиков и математиков не покладая рук трудились над тем, чтобы найти для каждого типа динамических систем «правильные» переменные, которые позволили всё удобно описать. Линейность- это свойство такой системы, реакция которой равна сумме реакций на отдельные воздействия (принцип суперпозиции). Линейные системы описываются линейными уравнениями, они просты, физически привлекательны, обладают замечательными физическими свойствами. Бритвой Оккама («не умножай сущностей без надобности») стремились отбросить нелинейные эффекты.

Мир линейных явлений логично построен, во многом предсказуем, доступен интуитивному пониманию (в ощущение и понимание на данном этапе человеческому сознанию даны параметры порядка). Мир нелинейных явлений широк, разнообразен; он познаётся с трудом.

Представление о нелинейном характере механических деформаций было высказано ещё в 17 веке Я. Бернулли как альтернатива линейному закону Гука.

Споры катастрофистов и эволюционистов – Бюффона и Ламарка, Кювье и Лайеля, также отражают различие этих двух главных моделей природных процессов. В жизни мы наблюдаем мир, отличный от мира Аристотеля, в нём нет дискретных категорий, нет фактической длящейся стабильности. В этом мире всё непрерывно изменяется, и идеальные формы евклидовой геометрии являются скорее исключениями, а не нормой.

Современная наука о Хаосе — это система представлений о различных формах порядка. «Хаос представляет собой более высокую форму порядка, где случайность и бессистемные импульсы становятся организующим принципом скорее, нежели более традиционные причинно-следственные отношения в теориях Ньютона и Евклида» (по Тихоплавам).

Вселенная как единая динамическая система

«Система - это совокупность, объединенная общей функциональной средой и целью функционирования, т.е. наделенная новым не свойственным отдельному элементу качеством.

Под открытой системой принято понимать систему, способную обмениваться с окружающим пространством (надсистемами и соседними системами) веществом, энергией и информацией» (Иванов О.П.).

Уже в начале XX века величайший русский мыслитель В.И. Вернадский писал о Земле, как о сложной открытой единой динамической системе.

Попытки ученых разделять «линейно» крупные системы на подсистемы без учета межсистемного взаимодействия были развенчаны уже в 19 веке великим математиком Анри Пуанкаре. Приведём более полную историю.

«Одним из наиболее изученных примеров может служить задача трех тел, которую с полным основанием можно назвать наиболее важной задачей в истории динамики. Одним из частных случаев задачи трех тел является движение Луны, испытывающей притяжение, как со стороны Земли, так и со стороны Солнца. Были предприняты бесчисленные попытки свести эту систему к интегрируемой, но в конце XIX в. Брунс и Пуанкаре доказали, что это невозможно. Их результат полной неожиданностью для современников и, по существу, возвестил о наступлении бесповоротного конца всех простых экстраполяций динамики на основе интегрируемых систем. Условимся называть интегрируемыми системами, такие которые можно представить в виде совокупности подсистем, при этом каждая такая подсистема изменяется в полной изоляции от других, независимо от них, совершая в процессе своей эволюции вечное и неизменное движение, которое Аристотель приписывал небесным телам. Открытие Брунса и Пуанкаре показало, что динамические системы не изоморфны. Простые интегрируемые системы допускают разложение на невзаимодействующие системы, но в общем случае исключить взаимодействия невозможно. Хотя в то время значение открытия Брунса и Пуанкаре не было оценено по достоинству, оно означало отказ от незыблемого убеждения в однородности динамического мира, в его сводимости к интегрируемым системам. Природа как эволюционирующая система с многообразно взаимодействующими подсистемами упорно сопротивлялась попыткам сведения ее к универсальной схеме, не содержащей к тому же времени» (Пригожин, Стенгерс, 2005).

«В 1965 году блестящий ученый, специалист в области квантовой механики, Джон Стюарт Белл опубликовал теорему, получившую название «О нелокальности причин». Теорема Белла подвергла сомнению всю теорию причинно-следственной связи. Белл утверждал, что отдельные причины не могут быть изолированы одна от другой. Он поддержал идею о том, что всё во Вселенной взаимосвязано. Это очень серьезное заявление. На сегодня уже тысячами экспериментов доказано, что теорема Белла является более точным описанием существующего порядка вещей. Его теорема гласит, что изолированных систем не существует, и что вся система, даже разделенная на части огромными расстояниями, между которыми отсутствуют сигналы, поля, механические силы, энергии и т. д., функционирует как Единая Система» (Тихоплав В.Ю. и др.).

Этот феномен можно объяснить с привлечением современной теории физического вакуума. Именно через энергонасыщенный физический вакуум (турбулентный эфир) может осуществляться взаимодействие каждой частицы с остальной Вселенной. Тем самым формулируется концепция о наблюдаемой Вселенной как единой нелинейной динамической диссипативной Вселенной, эволюция которой протекает в условиях мощных сторонних воздействий при перераспределении энергии между сильно взаимодействующими перестраивающимися подсистемами» (С.Ф. Тимашев).

Что такое «синергетика»?

Осознание сложного, нелинейного характера природных процессов, роли катастроф в эволюции; единства, взаимосвязи любого элемента, иерархичности всего Мироздания, недостатках понятия всех динамических систем как интегрируемых привели к созданию в конце XX нового научного направления – синергетики.

Изучение закономерностей эволюции открытых неравновесных систем и спонтанного возникновения в них порядка (их самоорганизации), несмотря на происходящее в них рассеяние (диссипацию) энергии и даже благодаря ему, привело И. Пригожина к созданию теории диссипативных структур, одного из направлений общего междисциплинарного движения, называемого в России вслед за немецким физиком Германом Хакеном синергетикой.

Термин «синергетика», в дословном переводе: “теория совместного действия”. Автор вкладывал в него два смысла. Во-первых, междисциплинарный подход, разработка которого требует совместных усилий специалистов. Во-вторых, это подход, изучающий возникновение новых свойств у сложной системы (процесс самоорганизации). Любой эволюционный процесс выражен чередой смен качеств - условных состояний порядка и хаоса в системе. В синергетике имеются универсальные методы и язык описания всех состояний, так как она развилась на базе достижений кибернетики, теории систем и те управления и включила все новое в области нелинейных исследований.

«Синергетика - это междисциплинарный подход, занимающийся проблемами самоорганизации сложных открытых систем. Данное определение, несмотря на некоторую лаконичность, содержит в себе достаточно сложных понятий, требующих пояснений. Под самоорганизацией принято понимать любое усложнение временной, пространственной или функциональной внутренней структуры сложной открытой системы в процессе эволюции, происходящее по правилам внутренней функциональной среды, имманентно присущим данной системе, без специфического воздействия из вне, навязывающего системе структуру или функционирование» (Г. Хакен). Синергетику при этом можно бы рассматривать как теорию возникновения новых качеств на микро- и макроуровнях, которые полностью взаимосвязаны. Такое определение базируется на исследованиях Г. Хакена, открывшего на примере лазерного излучения условия возникновения коллективного взаимодействия элементов системы на макроуровне, и А.П. Руденко, открывшего роль самоорганизации на микроуровне, как ведущей развития коллективных процессов макроуровня. (Иванов О.П.)

Значение ее состоит главным образом в стремлении найти ответы на самые глобальные вопросы устройства Мира. Лозунг: «Единая наука о единой природе».

Идеи синергетики, к сожалению, не очень быстро проникают в геологию, хотя они открывают большие перспективы. Стоит отметить прекрасные работы последних лет зарубежных и отечественных ученых: Turcotte D.L. “Fractals and chaos in geology and geophysics”, новосибирского ученого Ф.А. Летникова «Синергетика геологических систем», колоссальный труд группы ученых под руководством П.М. Горяинова и Г.Ю. Иванюка «Самоорганизация минеральных систем. Синергетические принципы геологических исследований», по сути, первое в России (а может быть и в Мире) универсальное издание по синергетике в геологии (приятно, что один из отцов-основателей синергетики, лауреат нобелевской премии по химии, И. Пригожин горячо поддержал данный проект). Также работы других исследователей, которые не были названы, перечислены в разделе «Литература» или нет, и конечно тех, о которых пока мало известно, но они черпают идеи из этого прекрасного необъятного мира Синергетики, которую можно назвать по выражению лауреата Нобелевской премии по физике Швингера инвариантом или законом законов (Ф.А. Летников).

В современном учебнике по общей геологии профессора Н.В. Короновского есть раздел, посвященный нелинейности в геологии.

«Новый диалог Человека с Природой». Выражение, приведенное в заголовке – это тезис И. Пригожина о необходимости кардинального переосмысления взаимоотношения человечества и Природы и выработки новой концепции на основании современной научной философии.

Принятый, по-моему, сегодня взгляд на актуальнейшие для цивилизации (а значит, и для науки) проблемы, как правило, не предполагают той общности подхода к восприятию «сущего» окружающего Мира, которого философы считают «наивысшей мудростью». А ведь геолог должен в своём сознании «объять весь Мир», впрочем, как и любой современный учёный!

Современная западная технократическая цивилизация, исторически поставила перед собой задачу покорения Природы, полному овладению её законами и установке искусственно управляемой, линейной «своей игры», очевидно, привела себя и остальное соблазнившееся человечество к кризису практически во всех сферах Жизни.

«Нелинейная» Природа не приемлет такого отношения. Такая идеология является недопустимой с точки зрения современной науки.

Чтобы понять сущность процессов, протекающих в современном сложном, нестабильном Мире, необходимо овладеть сложным мышлением.

С точки зрения современного междисциплинарного подхода к явлениям самоорганизации в сложных динамических неравновесных системах – синергетики, одним из основных подходов к решению глобальных проблем является не силовая политика (навязывание «своей игры»), а поиск способов коэволюции сложных социальных и геополитических систем. Поэтому, у мыслящего человека XXI века призыв «слиться с первозданной Природой» не должен вызывать усмешки или наивного недоумения.

В рамках этой концепции требуется осмысление геологии как отрасли народного хозяйства с позиций философии синергетики.

Синергетический подход к анализу взаимодействия природных систем

Весь мир, окружающий нас, состоит из структурированной материи (систем) и не структурированной материи (хаоса), которые взаимодействуют между собой. Например, нуклон представляет собой систему кварков. Атомное ядро состоит из системы нуклонов. Атом – это система нуклонов и электронов. Молекула – система атомов; кристалл и клетка – системы молекул. Порода – система кристаллов. Планетарное тело – система пород. Солнечная система состоит из Солнца, планет, спутников, комет, астероидов, метеороидов, метеоритов. Звезда – сложная излучающая система. Галактика – сложная система звезд, туманностей, скоплений видимого вещества и невидимого. Вселенная – система галактик.

Жизнь любой системы проходит в постоянных взаимодействиях с другими системами. Исходы таких взаимодействий могут быть благоприятными, но не исключаются и драматические ситуации с возникновением опасных природных процессов с последующими катастрофами. Например, столкновение теплых и холодных воздушных масс сопровождается возникновением подсистем атмосферных фронтов, циклонов и антициклонов с сопутствующими погодными изменениями. Удар астероида по поверхности Земли сопровождается гигантским взрывом и может привести к гибели биотических систем. Система большого кучевого облака сопровождается грозой, ливнями, градом. Взаимодействие систем тектонических блоков приводит к образованию подсистемы с чрезвычайно большой энергией, и в дальнейшем сопровождается энергетическим выбросом – землетрясением и т.д. Любая эволюционирующая система в течение своей жизни неоднократно встречается с кризисными ситуациями и преодолевает их, совершая некий скачок в своем устройстве для более эффективной адаптации. Любое взаимодействие природных систем приводит к обмену между ними веществом, энергией и информацией. При этом одна из систем является излучателем, а другая кумулятором или мишенью. В отдельных случаях взаимодействие сводится к возникновению пограничных подсистем, кумулирующих энергию обеих систем (пример с землетрясением). По мере накопления энергии кумулятивные системы переходят в неравновесное состояние с резким усилением динамики внутренних процессов, структурируются и диссипируют (рассеивают) избытки энергии. В этот период в системе присутствуют в значительной мере элементы хаоса и ее поведение и структуры могут быть охарактеризованы различными странными аттракторами (пространствами-притягателями). Динамичное неравновесное состояние порождает экстремальные диссипативные процессы, излучаемые системой.

Организация и самоорганизация

В предыдущей главе наш Мир был рассмотрен с позиций современного системного анализа. Интуитивно, наверное, каждый из нас рассуждает подобным образом. Так что такой подход не нов. Наша задача - выявить общие закономерности в сложных динамических процессах природных систем.

Для начала нужно обозначить вопрос организации и самоорганизации. Под термином «самоорганизация», являющимся базовым понятием синергетики, будем считать установление в диссипативной неравновесной среде пространственных структур, эволюционирующих во времени, параметры которых определяются свойствами самой среды и слабо зависят от пространственной структуры источника неравновесности (энергии, массы и т.д.), начального состояния среды и условиях на границах. Такое обобщенное понятие самоорганизации приводит в своей книге «Введение в синергетику: Хаос и структуры» саратовский ученый Д.И. Трубецков. Следующие главы данной работы будут посвящены разъяснению и рассмотрению этого удивительного явления Природы. Организация – структурообразование при специфическом внешнем воздействии.

В геологических системах встречаются оба типа структурообразования. К проявлениям самоорганизации могут без сомнения отнесены процессы кристаллизации, магматической и метаморфической дифференциации, тектоника, почти все типы складкообразования и т.д. Организация проявляется в процессах, обусловленных явлениями планетарного (изменениями климата, генерации магнитного поля Земли и т.п.) или ещё более крупного масштаба (22-летние циклы солнечной активности, падение крупных метеоритов). Другое дело, что и эти процессы часто оказываются результатом самоорганизации более крупной системы, как, например, это показали братья Николисы на основе анализа колебаний изотопного состава морских осадков, отражающих эволюцию климата на Земле (Иванов О.П.).

Глава II. Диссипативные системы

II.1. Понятие диссипативных структур

Из классической термодинамики известно, что эволюция закрытой (не обменивающейся с внешней средой веществом) системы обусловлена необратимым стремлением к состоянию равновесия (в пределе — к абсолютно однородному состоянию), характеризующемуся максимально возможным значением энтропии (Энтропия – термодинамическая функция, характеризующая меру разупорядоченности).

В качестве геологических иллюстраций такого рода процессов можно привести равновесный рост кристаллов, выветривание горного массива, кристаллизацию гранитного расплава. Кристаллизация гранитного расплава (конечно же, не всякого!), которая приводит к совершенно хаотическому (т. е. однородному) распределению минеральных зерен. В примере с выветриванием система также эволюционирует по пути к термодинамическому равновесию, поскольку из гетерогенного по строению массива, сложенного самыми разнообразными горными породами, возникает много более однородная песчаная масса.

Здесь сразу имеет смысл выделить в особую группу так называемые вынужденные

структуры, или штампы, к которым вплоть до недавнего времени относили все остальные геологические объекты (Горяинов, Иванюк, 2001). Вынужденные структуры очень близки к равновесным в том смысле, что их эволюция определяется пассивным стремлением к переуравновешиванию вслед за некоторыми изменениями во внешней среде. Соответственно, к вынужденным структурам применим упоминавшийся принцип Я. Седерхольма почти 100-летней давности: "у старого солдата больше шрамов, чем у молодого", что предполагает возможность путем "снятия" все более древних преобразований (эрозионных, тектонических, метаморфических, и т. д.) вычислить точку так называемого "термодинамического нуля", из которого и начала эволюционировать данная система.

Но современная термодинамика, начиная с И. Пригожина, описывает природные системы, как так называемые открытые активные системы, поведение которых не может быть представлено как эволюция в сторону какого-то выделенного устойчивого состояния с минимумом энергии и максимумом энтропии. Их активность обусловлена непрерывным притоком энергии от внешних источников (например, накачка горного массива эндогенной или наведенной упругой энергией) или ее производством внутри самой системы (например, саморазогрев горных пород за счет экзотермических реакций минералообразования).

Рассмотрим вслед за И. Р. Пригожиным неизолированную систему, обменивающуюся с внешней средой энергией и/или веществом. Изменение её энтропии можно представить суммой двух членов, обусловленных внутренними процессами d_iS и потоками извне d_eS:

dS/dt= d_iS/dt+ d_eS/dt,

причем какого-либо физического закона, который определял бы знак изменения энтропии в неизолированной системе не существует. Соответственно, если член d_eS отрицателен и по величине превосходит d_iS ,то определенные стадии эволюции могут происходить при общем понижении энтропии. Такая ситуация способна реализоваться только вдали от равновесия, поскольку в равновесном состоянии по второму началу всегда преобладает член d_iS.

Так как сверхкритическая отдача энтропии возможна лишь при наличии способствующей тому внутренней структуры, то при определенных условиях в таких системах возникают пространственные или временные регулярные образования, само существование которых поддерживается только за счет оперативного рассеяния (диссипации) поступающей извне энергии. Любые системы, полная энергия которых при движении убывает, переходя в другие формы (например, механическая энергия в теплоту), получили название диссипативных систем. Например, если в ламинарный поток жидкости привнести дополнительную энергию, это будет скомпенсировано увеличением ее диссипации за счет передачи от крупномасштабных турбулентных вихрей к всё более и более мелкомасштабным, где уже начинает играть роль вязкость, переводящая механическую энергию вихрей в тепло. Эти структуры, получившие по предложению И. Р. Пригожина название диссипативных структур, чрезвычайно широко распространены в живой природе.

II.2. Эксперимент Бенара

Известный эксперимент, на котором И. Пригожин развивал свою теорию - возникновение засчет упорядоченной конвекции в подогреваемом снизу слое жидкости шестигранных призматических ячеек – ячеек Бенара.

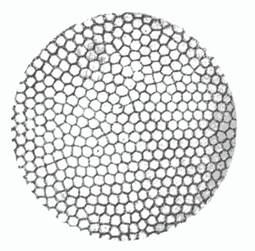
Структура Бенара как раз и является простейшей диссипативной структурой. Она позволила системе уцелеть в потоке поступающей извне энергии путем максимально эффективной ее диссипации. «В классической термодинамике тепловой поток считался источником потерь. В ячейке Бенара тепловой поток становится источником порядка» (И. Пригожин).

Как показал И. Р. Пригожин, в диссипативных системах при данных внешних условиях, препятствующих достижению системой состояния термодинамического равновесия, из возможных стационарных состояний выбирается таковое с минимумом производства энтропии (теорема Пригожина). Это заключение связано с принципом наименьшего рассеяния энергии Л. Онсагера, показавшего в 1931 г., что в неравновесных термодинамических системах реализуется то из возможных состояний, которое требует минимальных энергетических затрат (Горяинов, Иванюк, 2001).

Диссипация энергии в жидкости зависит от отношения площади ячейки к ее объему (удельной поверхности): чем меньше это отношение, тем меньше диссипация. Нетрудно убедиться, что наименьшей удельной поверхностью характеризуются именно шестигранные ячейки. Иными словами, в полном соответствии с вышеизложенными принципами, в эксперименте Бенара реализуется наиболее энергетически выгодная конфигурация ячеек.

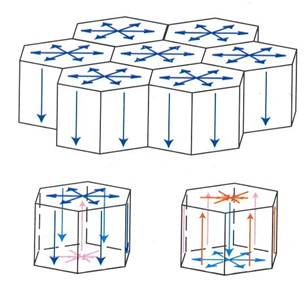
Направление движения жидкости в ячейках Бенара. Красными стрелками обозначены потоки более горячей жидкости, синими – более холодной.

В качестве иллюстраций к сказанному рассмотрим закономерности образования ячеистых структур в различных геологических системах.

II.3. Геологические аналоги «бенаров» и другие полигональные структуры

II.3.1. Мёрзлые грунты

Полигональная делимость, образовавшаяся в результате

оттаивания грунта на г. Ньоркпахк (Хибины) (фото Горяинова П.М.)

Полигональная делимость мерзлых грунтов являет собой геологический пример самоструктурирования по конвективному механизму, по сути, ничем не отличающемуся от такового классических ячеек Бенара. Их появление обусловлено быстрым оттаиванием

почвы, сопровождающимся упорядоченной конвекцией воды в ее приповерхностных слоях. Единственное отличие от эксперимента Бенара заключается в том, что более теплая поверхность в этом случае находится сверху; конвекция же осуществляется благодаря инверсии плотности воды (менее плотная при 0 ^оС холодная вода поднимается вверх, нагревается до +4 ^оС, увеличивая свою плотность, и снова опускается вниз).

Остается заметить, что механизм образования ячей Бенара активно привлекается "теорией плит" в качестве базиса движения континентов и "теорией мантийных плюмов" для объяснения возникновения и эволюции "горячих точек" (Turcotte, 1997)

II.3.2. Ячеистый рост кристаллов

При росте кристалла из расплава растущая и грань выделяет теплоту кристаллизации, создающую вблизи границы кристалл-расплав тонкий слой более горячей жидкости. Любой выступ, который по какой-то причине оказался за пределами этого слоя, начинает расти все быстрее и быстрее, выделяя теплоту кристаллизации и подавляя соседние выступы. В результате образуется ячеистая поверхность грани, а максимальным проявлением этого процесса является дендритный рост.

Ячеистая структура фонолита (вулканического эквивалента нефелиновых сиенитов) (Хибины)

Точно такая же шестиугольная делимость может возникнуть и при росте кристалла из раствора, хотя в этом случае эффект обусловлен уже не температурным, а концентрационным градиентом. Грань растущего кристалла, поглощая вещество из раствора, создает вблизи фронта кристаллизации слой раствора относительно пониженной концентрации. Выступ, "дотянувшийся" до более концентрированного раствора оказывается в более выгодных условиях для роста по сравнению с окружающими его участками. Далее начинается конкуренция между такими выступами, приводящая в конце концов к ячеистой поверхности рассматриваемой грани и, далее, к образованию дендритов. На горизонтально расположенных гранях образование ячеек может усиливаться за счет механизма Бенара, поскольку обедненный примесями менее плотный слой раствора вблизи грани создает еще и гравитационную неустойчивость. Подъем раствора происходит в центральных выпуклых частях ячеек, а опускание — в промежутках между ними (по Горяинову П.М.).

II.3.3. Контракционные структуры

Наиболее ярким примером контракционных структур являются ячеистые лавовые покровы. В базальтах очень известны шестигранные колонны (столбчатые отдельности).

Вполне возможно, что на начальных этапах зарождения этих структур здесь был задействован и конвективный механизм Бенара, поскольку иначе пока трудно объяснить одновременность заложения всех трещин (Горяинов, Иванюк, 2001). И уже после заложения правильной сети трещин они развивалась вглубь по мере того, как базальтовые колонны сжимались под охлаждающим действием просачивающейся воды.

Столбчатая отдельность в базальтах Шестигранная полигональная делимость базальтов Словакии (фото Т.М. Гептнер) (Восточные Карпаты) (фото Горяинова П.М.)

Некоторые ученые предполагают, в частности С.Ф. Тимашев, наличие во внешнем ядре диссипативных структур Бенара, но засчет турбулентной конвекции (которая возможна, и наверно реальна), структуры нерегулярные, несимметричные (валы, вихри).

Рассмотренные выше диссипативные геологические структуры визуально схожи с простейшей диссипативной структурой – ячейками Бенара. И поэтому возможен похожий механизм их образования. Это всего лишь один класс огромного разнообразия этих необычных структур.

Оказывается, несмотря на различие природы диссипативных структур (гидродинамические, химические и др.) и типов возникающих в них структур, имеются следующие четыре необходимых по Пригожину (затем по Эбеленгу) условия образования диссипативных структур:

-система является термодинамически открытой

-отклонение от равновесия превышает критическое значение

-динамические уравнения системы нелинейны

-микроскопические процессы происходят кооперативно

Из этих условий видно, что практически все геологические системы диссипативны и применение современной теории диссипативных структур очень уместно.

В конце главы стоит привести краткое изложение теории диссипативных структур:

И. Пригожин и его ученики показали, что открытые системы вдали от равновесия могут эволюционировать к некоторому новому состоянию в силу того, что микрофлуктуации в них приобретают кооперативный, когерентный характер. Новое состояние системы может существовать неопределенно долгое время, при этом в системе возникают новые структуры, которые получили название диссипативных. К ним относятся известные гидродинамические неустойчивости Бенара, периодические реакции Белоусова-Жаботинского, и др. Их возникновение “антиэнтропийно” в том смысле, что оно сопровождается общим снижением энтропии системы (за счет обмена веществом и/или энергией с внешней средой).

Усиление флуктуаций с удалением от состояния равновесия ведет к спонтанной потере устойчивости системы. В критической точке, называемой точкой бифуркации, система либо разрушается (превращается в хаос), либо вследствие преобладания когерентного поведения частиц в ней происходит образование диссипативных структур. Путь своего дальнейшего развития система выбирает под воздействием случайных факторов, поэтому невозможно предсказать ее конкретное состояние после точки бифуркации и характер возникающих диссипативных структур.

Наиболее важным свойством диссипативных структур является снижение их пространственной симметрии в точке бифуркации. Снижение симметрии порождает более высокую упорядоченность и, следовательно, снижает энтропию системы. Эволюция есть последовательное образование диссипативных структур в состояниях, далеких от термодинамического равновесия. (Неравновесность есть то, что порождает порядок из хаоса.) При этом, несмотря на повышение в процессе саморазвития уровня организации и сложности систем, с течением времени происходит ускорение эволюции.

Некоторые ученые (Кравченко Н.С. и др.) связывают универсальный принцип симметрии-дисимметрии Кюри и теорию диссипативных структур. В частности утверждается, что система, находясь в точке бифуркации подвержена этому принципу. Он накладывает определенные морфологические ограничения на дальнейшую эволюцию системы. Этот принцип дает возможность предсказывать в общем случае морфологические характеристики продуктов эволюции в неживой природе на основе полного описания симметрийных характеристик среды и происходящих в ней процессов. И делается вывод о возможности прогнозировать пути эволюции. Но пока эта очень революционная точка зрения не доказана.

Такыры (глинистые пустыни)

Глава III. Автоколебания

III.1. Понятие автоколебаний

Вышеупомянутые системы, в которых диссипация энергии компенсируется её притоком извне, называются активными. В таких системах и возникает очень интересный процесс – автоколебания. Они могут возникнуть при скачкообразном переходе системы на новый энергетический уровень (в новое стационарное состояние) из-за сильного воздействия извне.

Термин автоколебания ввёл А.А.Андронов в 1928 году в своей блестящей работе «Предельные циклы Пуанкаре и теория автоколебаний». Автоколебания – это незатухающие колебания в диссипативной системе, поддерживаемые внешним источником энергии (положительная обратная связь). Для возникновения автоколебаний необходимо: колебательная система, источник энергии, нелинейный элемент, регулирующий поступление энергии в систему. Известный пример – механические часы, в которых функции обратной связи, усилителя и ограничителя выполняет единый узел – балансир с анкером. Если в любом периодическом процессе выявить данные условия – можно смело говорить об автоколебательном процессе. А их в Природе достаточно много.

Красивую интерпретацию колебательных химических (впрочем, она имеет общий характер) процессов дал Л.А.Блюменфельд: «Есть древняя легенда. У ворот города стражники останавливали путников и спрашивали: «Зачем вы сюда пришли?». Отвечающих правду закалывали, а лгущих вешали. Нашелся умный человек, который ответил: «Я пришел сюда, чтобы вы меня повесили!». И начался колебательный процесс. Если он сказал правду, то его надо повесить, но тогда окажется, что он сказал правду… Стражники колебались между двумя крайними решениями, не принимая ни одного из них. В этом парадоксе, как и во многих аналогичных, вывод из утверждения противоречит утверждению.

Механизм возникновения колебательных химических реакций весьма близок к изложенному. Для того чтобы в результате химических реакций в открытой системе могли происходить незатухающие колебания концентраций промежуточных соединений, необходимо, чтобы в результате одного из этапов процесса появлялись вещества, ингибирующие стадии, предшествующие их появлению. Надо, чтобы результат процесса противоречил процессу, нужна отрицательная обратная связь. Конечно, для реализации колебательного процесса нужна не только отрицательная, но и положительная связь ».

Рассмотрим более подробно реакцию Белоусова-Жаботинского, которая порождает удивительное разнообразие временных и пространственных структур, сопоставимых по облику с разного рода геологическими объектами. Она представляет собой процесс окисления органического восстановителя (лимонная, яблочная, малоновая кислоты) бромат-ионами в присутствии катализатора – иона переходного металла, например, Mn²⁺. В зависимости от скорости непрерывной подачи реагентов, смесь будет периодически менять свой цвет. Такое поведение можно рассматривать как химические часы – устройство для измерения времени при помощи внутренней динамики системы.

Последовательные стадии реакции Белоусова-Жаботинского. Взято с сайта Главной химической лаборатории университета г. Сиген, Германия (Горяинов, Иванюк, 2001)

Эта реакция является классическим примером химических автоколебаний. Рассмотрим теперь геологические примеры.

III.2. Автоколебания в геологических системах

Явление периодической кристаллизации магматического расплава - пример автоколебательного процесса. С ним исследователи связывают возникновение расслоенных интрузий (Горяинов, Иванюк, 2001).

Автоколебания появляются в модели с сухим трением (Вадковский В.Н., Захаров В.С.), демонстрирующем динамику взаимодействия литосферных блоков между собой в процессе землетрясения. Можно выделить колебательную систему блоков, источник энергии, нелинейный закон, регулирующий поступление энергии в систему.

Автоколебания климата

Ещё в 1884 году А.И. Воейков выявил положительную обратную связь между оледенением и температурой, сходною с рассмотренными примерами. Если за счет локального похолодания несколько увеличилась площадь полярных льдов, исключительная отражательная способность льда нелинейно уменьшит количество поглощенной солнечной энергии. Это, в свою очередь, приведет к уже глобальному похолоданию и дальнейшему распространению ледяных шапок. С другой стороны, рост ледников понижает влажность атмосферы, являющуюся необходимым условием их роста (отрицательная обратная связь).

Итак, рассмотренные примеры показывают важность и распространенность автоколебательных процессов, как одного из атрибутов перехода на новый энергетический уровень открытых динамических системы в Природе.

Необычность таких систем заключается в том, что при учете всего нескольких основных параметров можно получить математическую модель, достаточно хорошо согласующуюся с данными непосредственных исследований. Но стоит отметить, что автоколебательные системы всегда нелинейны. Следовательно, при малейшем изменении параметров в «подходящий» момент может оказаться достаточным, чтобы процесс прекратился. Как тут не вспомнить знаменитый «эффект бабочки» и рассказ Р. Брэдбери «И грянул гром» (1963), где маленький проступок колоссально и необратимо изменил будущее всей Гиперсистемы.

«Вот тут самое время вспомнить про динозавров и задуматься. Оказывается, вовсе необязательна глобальная катастрофа вроде падения астероида, чтобы с ними покончить.

Всё, конечно, не так просто в Природе. Но стоит обратить внимание на то, что даже простая система обнаруживает вовсе непростое поведение – это следствие её нелинейности» (В.Н. Вадковский, В.С. Захаров, 2001).

В конце стоит отметить, что практически все регулярные структуры периодическими, по сути, не являются, а выглядят достаточно хаотичными. С другой стороны, они в каком-то смысле самоподобны. Топологические особенности самоподобных структур рассматриваются в рамках бурно развивающегося междисциплинарного направления – геометрии фракталов.

Глава IV. Фрактальная геометрия Природы

Красота – это бесконечность, выраженная

в законченной форме.

Ф. Шеллинг

IV.1. Понятие «фрактала»

Геометрическое описание объектов в геологии нашло отражение в таких базовых понятиях как морфология, структура, текстура, дислокация и многих других. По традиции основой интуитивного понимания геометрии геологических структур служат Евклидовы фигуры: прямые, окружности, сферы, плоскости и т.д., а любые отклонения от этих форм объясняются некими деструктивными процессами (складчатость, разломы и пр.). Такой подход, конечно, не совершенен.

В 1975 году французский ученый Бенуа Мандельброт произвел революцию в геометрии, введя понятие фрактала (от латинского fractus – «дробный») для обозначения нерегулярных, но самоподобных фигур, которыми он занимался. Его, ставшая уже классической, работа "Фрактальная геометрия природы" открывается следующими словами: " Почему геометрию часто называют "холодной" и "сухой"? Одна из причин заключается в ее неспособности описать форму облака, горы, береговой линии или дерева. Облака - не сферы, горы - не конусы, береговые линии - не окружности, древесная кора не гладкая, молния распространяется не по прямой. В более общем плане я утверждаю, что многие объекты в Природе настолько иррегулярные и фрагментированы, что по сравнению с евклидовыми фигурами - термин, который в этой работе означает всю стандартную геометрию, - Природа обладает не просто большей сложностью, а сложностью совершенно иного уровня".

«Новая геометрия способна описать многие из неправильных и фрагментированных форм в окружающем нас мире и породить вполне законченные теории, определив семейство фигур, которые я называю фракталами».

Если говорить в терминах естествознания, появилось новое удачное приближение к Природе на языке математики, хотя идею самоподобия малого в большом давно высказывали философы. Интересно - философы опережают конкретные математические разработки.

В 1983 году Б. Мандельброт писал: «Ученые будут поражены и восхищены, обнаружив, что не только те несколько форм, которые они называют словами зернистый, гидроподобный, прыщеватый, рябой, разветвленный, водорослеподобный, странный, запутанный, извилистый, волнистый, клочковатый, морщинистый, но и им подобные отныне можно будет строго и уверенно рассматривать количественным образом».

Эти слова, так знакомые геологам, в современной математике объясняются теорией фракталов – плодотворно развивающейся области знаний, охватывающей колоссальное количество объектов, состоящих из частей, которые в каком-то смысле подобны целому – самоподобны, - причем это подобие может быть как геометрическим, так и статистическим.

Действительно, очень многое в Природе характеризуется бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько угодно раз. Так, дерево имеет ветви, от которых отходят ветви поменьше, от тех - еще меньше и так вплоть до самых тонких отростков. Если сфотографировать само дерево и ветки разных размеров, убрать все, что говорит о масштабе изображений, и сравнить их друг с другом, скорее всего, мы не сможем определить истинное соотношение этих объектов. Точно так же ведут себя речные сети на картах разного масштаба или, скажем, дендриты. Еще одним типом фрактальных объектов являются горы, форма пиков и конфигурация цепей которых повторяются в очень широком интервале масштабов. Более строгое определение фрактала связано с очень важным понятием: его дробной размерностью. Звучит удивительно, но в дальнейшем можно будет понять глубокий смысл этого понятия.

IV.2.Фрактальная размерность

Топологическая (евклидова) размерность фигуры определяется числом координат, требуемых для однозначного определения положения на ней любой её точки (в случае описания динамической системы (фазовое пространство) – количество переменных).

Следовательно, точка – нуль-мерный объект, линия – одномерный, поверхность – двумерный, объёмная фигура – трёхмерный объект.

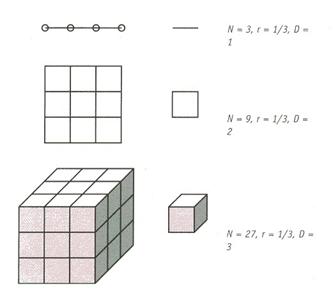
Если разделить отрезок на любое число N равных частей, то каждую часть можно считать копией всего отрезка, уменьшенного в 1/r раз. Видно, что N и r связаны соотношением Nr=1. Точно так же, если квадрат разбить на N равных квадратиков с площадью, в 1/r² раз меньшей площади исходного квадрата, N и r будут связаны соотношением Nr²=1, а в случае такой же операции с кубом: Nr³=1. Размерность D этих фигур равна степени при коэффициенте подобия r:

Nr^D=1

Отсюда,

D=(lgN)/(lg1/r)

Вычисленная таким образом размерность называется размерностью подобия D_S. Оказывается, существует обширный класс объектов, характеризующихся дробной величиной D_S. В этом случае D_S выступает в качестве одной из разновидностей фрактальной размерности (в частности эта носит название размерности Хаусдорфа-Безиковича), а сами объекты называются фракталами.

В качестве простейшего примера таких объектов рассмотрим множество Кантора, названного по имени Георга Кантора, описавшего его в 1883 году. Для построения возьмем единичный отрезок [0,1], разделим его на три равные части и выбросим средний интервал (1/3,2/3). Каждый из двух оставшихся снова разделим на три части, выбросим из них средние и так далее.

D_S=log2/log3≈0.63092,

т.е. представляет собой объект, промежуточный между точкой и линией.

Регулярное и нерегулярное множество Кантора

Рассмотренный пример нахождения фрактальной размерности является возможным только для так называемых регулярных фракталов. Но в Природе скорее можно встретить нерегулярные, случайные фракталы, например, в данном случае построение множества Кантора будет немного иным. После разбиения отрезка на три части выбрасывается любая (необязательно средняя) из них, и процесс повторяется. Многие геологические структуры относятся именно к этому типу фракталов: множество зерен акцессорного минерала в горной породе и т.д.

Другим мощным методом нахождения фрактальной размерности является клеточный метод. Он основан на поиске зоны скейлинга в объекте, покрытом N кубиками со стороной s:

N~s^-D

Отсюда логарифмируя и аппроксимируя функцию, находим D – фрактальную размерность.

Существуют ещё более сложные и совершенные методы нахождения фрактальной размерности.

Попробуем осмыслить понятие дробной размерности и расширить это понятие на остальные “измерения”.

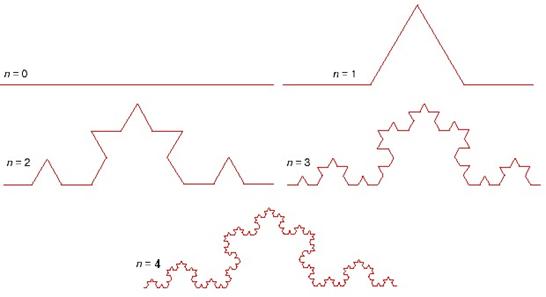
Снежинка Коха

Каждая сколь угодно малая часть фрактальной линии содержит в себе уменьшенную копию всей линии. И значит, это уже не линия в евклидовом смысле «длина без ширины», а нечто большее, некая «толстая линия». То есть фрактальная линия – уже не одномерная евклидова линия, но ещё и не двухмерная поверхность. Фрактальная линия есть некая «толстая линия» с дробной размерностью 1<D<2. Чем более изломана фрактальная линия, тем ближе к 2 её фрактальная размерность. Соответственно, и фрактальная поверхность – это уже не поверхность размерности 2, но ещё и не объёмное тело размерности 3, некая «вспенённая» поверхность.

Можно сказать, что фрактальная (дробная) размерность показывает, «насколько плотно точки заполняют пространство. Фрактальная размерность позволяет количественно описывать неупорядоченные структуры. Итак, фракталы – самоподобные объекты, характеризующиеся дробной размерностью.

Фракталы условно делятся на регулярные и нерегулярные. Рассмотренные выше – регулярные. Самоподобие проявляется напрямую: любая часть есть уменьшенная точная копия целого. Значительно сложнее и разнообразнее нерегулярные фракталы. Самоподобие: часть есть не точная, а похожая деформированная копия целого. Нерегулярные фракталы встречаются намного чаще в Природе.

«Фрактальная геометрия занимается изучением инвариантов группы самоаффинных преобразований», т.е. свойств, выражаемых степенными законами, что делает её мощным средством для анализа огромного количества геологических процессов, описываемых также степенными законами.

IV.3.Фракталы в геологии

IV.3.1.Топология рельефа и речных сетей

Тот факт, что береговые линии континентов не могут быть представлены в виде гладких кривых с соответствующей размерностью, равной единице, ещё в 1939 году установил английский метеоролог Л.Ф. Ричардсон при попытке как можно более точно определить периметр Британии. Оказалось, что если измерять длину L береговой линии этого острова с последовательно уменьшающимся раствором r, то она будет возрастать по степенному закону в соответствии с формулой:

L(r)~r^-0.25

С этого факта и начал свои исследования Б. Мандельброт – создатель фрактальной геометрии.

Впоследствии было показано, что подобным образом ведут себя многие, если не все прочие контуры земного рельефа: изолинии высот вообще и береговые линии в частности, очертания пещер и еще многие другие. Все они являются объектами, промежуточными между линией (D=1) и поверхностью (D =2), хотя топологическая размерность как и любых линий равна единице. Были подсчитаны фрактальные размерности побережий: Британия – 1.24, Австралия – 1.1, Южная Африка – 1.04, Япония – 1.4, Норвегия – 1.5 . Как и следовало ожидать, большая визуальная извилистость выражается большим значением D. Фрактал – мера «неправильности».

Любой топографический профиль непрерывно формируется динамическими процессами разрушения и созидания, поэтому можно предположить, что он также является фракталом. Этот вопрос был изучен и по данным Вадковского В.Н. и Захарова В.С.: район Гималаи-Тибет имеет размерность 1.67, южные районы озера Байкал – 1.674, Центральная Африка – 1.704, Северная Атлантика – 1.484 и т.д. А высокая расчленённость рельефа говорит о интенсивной эндогенной подпитке этого района. Это очень важное следствие теории фракталов, дающее геологам количественно сравнивать тектонические режимы регионов.

Помимо геометрии изолиний рельефа интересно изучение фрактальной размерности речных сетей. По теореме Онсагера (см. главу I), система стремится к минимизации диссипации энергии. Поэтому, по мнению исследователей, речная сеть, как диссипативная система, имеет фрактальную структуру, как энергетически наиболее выгодную. Более подробно речные сети будут рассмотрены в главе IV.3.

IV.3.2.Фрактальность геологических тел: от кристаллов до залежей полезных ископаемых

Дендриты – классический пример фрактальной организации минерального индивида. Переходя вверх по иерархии литосферы можно отметить фрактальность структур и текстур горных пород. Некое самоподобие выявляется в друзах и других производных геометрического отбора.

Дендриты гетита в трещине известняка

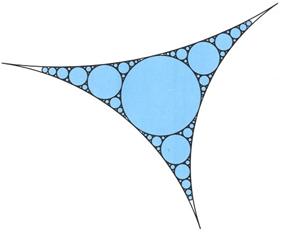
Такие сложные объекты как брекчии могут быть самоподобны в интервале масштабов не менее пяти порядков, а за кажущейся хаотичностью их строения просматриваются строгие закономерности. Последнее хорошо иллюстрирует классический фрактал «салфетка Аполлония», подробно рассмотренный Б. Мандельбротом во «Фрактальной геометрии Природы». Его построение начинается с трех касающихся окружностей произвольного диаметра, между которыми будет заключен округлый треугольник с углами в 0^o. В этот треугольник вписывается окружность наибольшего возможного диаметра, образующая ещё три округлых треугольника меньшего размера. Бесконечное повторение описанной процедуры порождает «салфетку Аполлония». Интересно, что большие области океанических льдов океанических льдов фрагментируются подобно каскаду Аполлония. Даже был сформулирован «эффект расплывающейся льдины»: каждый фрагмент, невзирая на его размеры, может быть с достаточной долей уверенности составлен с соседними, пусть и достаточно удаленными фрагментами. Согласно теории неравновесной фрагментации, образование фрактальной делимости горных пород обусловлено тем, что вероятность разрушения неоднородной среды возрастает, когда взаимодействуют обломки одинакового размера (т.е. вероятность того, что крупный обломок раздавит мелкий и, тем более, наоборот, намного ниже, чем вероятность взаимного разрушения близких по размеру пород). В результате, близкие по размеру соседние обломки разрушаются и никакие два одинаковых фрагмента не встречаются совместно (Sammis et al., 1986).

Слоистость и метаморфическую полосчатость можно сравнить с чередованием случайных множеств Кантора разных минералов. Ученые делают успешные попытки применить фрактальную геометрию для анализа сложности строения месторождений полезных ископаемых.

IV.3.3. Фрактальные характеристики процесса разрушения горных пород

Изучая процессы разрушения горных пород, исследователи пришли к выводу, что данный процесс нелинейный. Закон Гука F=-kx действовал только на начальном этапе деформации. При достижении некоторого порогового значения, закон линейный закон переставал действовать, и происходило перераспределение напряжений (разрыв связи), результатом которого становилась разветвленная система трещин. Эксперименты проводились с двумя видами деформаций, встречающихся в Природе – растяжение и сдвиг. Характерные конфигурации трещин в обоих случаях имели фрактальную структуру с размерностью 1.62-1.64. «Фрактальная природа трещин свидетельствует о непредсказуемости направления развития трещин, а равенство фрактальных размерностей систем трещин при растяжении и сдвиге говорит о том, что, изучая направления трещин, нельзя определить, каким типом внешнего воздействия это вызвано». «Естественные границы разделов (трещины-разломы-рельеф) имеют фрактальный характер» (Вадковский В.Н., Захаров В.С.).

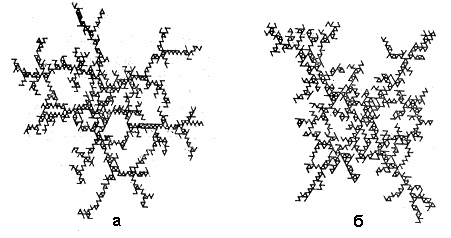
Фрактальность трещин при: а – растяжении; б – сдвиге (по данным Вадковского В.Н., Захарова В.С.)

IV.3.4. Фрактальные характеристики сейсмичности

По данным современных каталогов землетрясений разными авторами определена фрактальная природа сейсмического режима различных регионов. Этот вывод сделан на основе анализа графика повторяемости землетрясений (зависимость количества землетрясений от их магнитуды). По данным Вадковского В.Н. и Захарова В.С., Курило-Камчатский район – магнитуда (M) 4.4 – фрактальная размерность – 1.509; Суматра-Филлипины – M=4.4, D=1.439; Альпийская Европа – при М=2.1, D=1.929 и т.д.

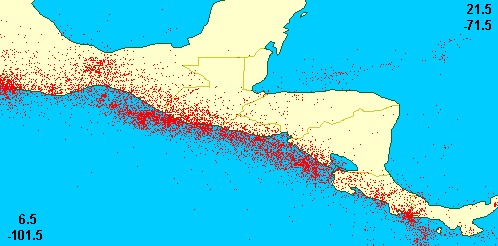
Фрактальное распределение очагов землетрясений

области Центральной Америки (по данным Вадковского В.Н., Захарова В.С.)

Фрактальное строение разломных сетей определяет особенности фрактальной временной динамики землетрясений и наоборот. «Приведенные значения фрактальной размерности сейсмичности свидетельствует о единстве процесса взаимодействия блоков геологической среды вне зависимости от конкретного механизма тектонической деформации».

А.А. Наймарк в своей статье «Фрактальность геологической среды и проблема прогнозируемости сейсмогенного макроскалывания» делает вывод невозможности прогноза землетрясений на основе традиционной модели геологической среды (квазисплошной, несамоподобно структурированной и т.д.). Т.к. по последним научным данным литосфера глубоко иерархизованная (многоуровневая), самоподобная, глубоко дискретная с фрактальной структурой среда. Необходимы новые идеи в этой области.

IV.3.5. Прикладное значение теории фракталов в геологии:

Фрактальный предвестник тайфунов

Метод основан на анализе фрактальной размерности изолиний температуры в облачных кластерах и является мощным инструментом для диагностики крупномасштабных когерентных процессов в геофизике (по материалам «Проблемы геофизики XXI века»).

IV.3.6. «Геофизическое» заключение

С точки зрения современной физики, открытая сложная система в процессе эволюции неизбежно приходит к состоянию самоорганизованной критичности (подробнее ниже в одноименной главе), для которого характерна иерархическая организация неоднородностей (фрактальность) и степенные законы во временных распределениях меняющихся параметров. И земная кора в целом, и отдельные её элементы, относятся к классу подобных систем. Соответственно, мы находим фракталы в различных геологических структурах на различных пространственных уровнях и получаем фрактальные ряды геофизических данных.

До сих пор были рассмотрены фракталы, как статистические фигуры. Однако геология – наука историческая и должна интересоваться особенностями процессов, приведших к фрактальному строению практически всех объектов её изучения. В следующей главе будут рассмотрены последние достижения в исследованиях сложных природных динамических процессов.

Глава V. Детерминированный хаос и самоорганизованная критичность

Синергетика открывает совершенно новые горизонты познания: сверхсложная, многомерная, внешне совершенно беспорядочная среда может описываться небольшим числом фундаментальных понятий и образов, отражающих общие тенденции развертывания в ней процессов самоорганизации. Столь оптимистический взгляд на перспективу изучения сложных (хаотических) геологических структур дает нам теория самоорганизации.

Изучая какие-либо хаотические структуры, уже можно предположить, что рассматриваемые системы только на первый взгляд похожи на последовательность случайных событий (т.к. в Природе ничего случайного нет), а их эволюция является некоторым динамическим эквивалентом фрактала.

V.1. Аттракторы

В 1961 году Эдвард Лоренц, ученый метеоролог, занимающийся моделированием конвективных потоков в атмосфере, сформулировал вышеупомянутый «эффект бабочки», суть которого заключается в существенной зависимости хаотической системы от начальных условий. Но это не стало сенсацией – об этом в своих работах писал великий Анри Пуанкаре ещё в конце 19 века. А вот компьютерное моделирование процесса привело к впечатляющему открытию. Лоренц в своей модели погоды обнаружил не только её чрезвычайную хаотичность. Он обнаружил некий порядок, выдающий себя за случайность – детерминированный хаос.

Не приводя сложных моделей, можно описать хаотическую систему, обнаруженную Лоренцом, как подогреваемое снизу и охлаждаемое сверху «водяное колесо» - тонкое кольцо, заполненное жидкостью.

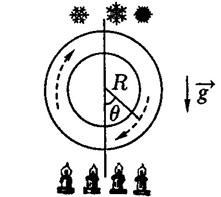
Допустим, что в данный момент времени жидкость движется по часовой елке. При достаточно большой разнице температур снизу и сверху сила Архимеда становится большой и водяное колесо ускоряется настолько, что остывшая вверху часть жидкости быстро «проскакивает» горячее основание, не успев нагреться. Этот объем жидкости уже не может подняться до верха петли и приостанавливается, поскольку сила Архимеда теперь недостаточна, чтобы преодолеть силу вязкости и гравитацию. Опускающаяся (правая) часть жидкости теплее, и поэтому легче, поднимающейся. Из-за торможения кольца жидкость в его основании нагревается и поднимается, но уже в противоположном направлении, так как давление справа меньше, чем слева. И жидкость начинает двигаться против часовой стрелки. Потом все повторяется в обратном порядке. Поскольку величина нагрева единицы объема жидкости, скорость вращения кольца, его ускорение зависят от очень тонких деталей начального движения, при большой разности температур снизу и сверху смены направлений движения оказываются случайными (хаотичными).

Движение данной системы описывалось тремя уравнениями с тремя неизвестными. Построив компьютерную модель, он получил на графике нечто бесконечно запутанное, но никогда не повторяющееся. Траектория не пересекает саму себя, образуя лишь новые и новые петли. Данный объект был назван аттрактором Лоренца или Странным Аттрактором. Аттрактор динамической системы – множество точек или подпространство в фазовом пространстве, к которому асимптотически приближается траектория системы. Аттрактор – притягивающее множество (attract – с англ. «привлекать», «притягивать»).

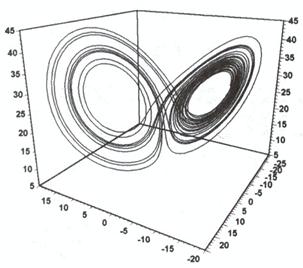
Странные аттракторы представляют собой крайне необычные математические объекты. С одной стороны, для их описания используются системы дифференциальных уравнений, в которых все определено, детерминировано и не содержится никаких стохастических членов. А с другой стороны - поведение решений такой системы уравнений на продолжительном временном интервале приобретает хаотический, непредсказуемый (внутри области аттрактора) характер. Полностью детерминированная, с точки зрения традиционных представлений, система, тем не менее, порождает индетерминированный, хаотический процесс, И самое интересное, что в природе обнаружены явления, моделировать которые можно только с помощью указанного типа аттракторов. Причем явления такого рода наблюдаются отнюдь не только в экзотических областях физической реальности, вроде микро - или мегамира, но и на масштабах, соразмерных масштабу человека. Например, изменения погоды, как правило, моделируются именно странными аттракторами, которые в фазовом пространстве изображают смену состояний метеорологического объекта.

И. Пригожин: «При исследовании того, как простое относится к сложному, мы выбираем в качестве путеводной нити понятие «аттрактора», то есть конечного состояния или хода эволюции диссипативной системы».

Странный аттрактор – притягивающее множество в фазовом пространстве, в котором расположены хаотические траектории. Множество, соответствующее странному аттрактору, фрактально.

Было установлена размерность климатического аттрактора D=3.1 (привлекается четвертое измерение) на основании исследований кернов льдов Антарктиды на соотношение изотопов O¹⁸/O¹⁶ на интервале последнего миллиона лет. (И. Пригожин). Тот факт, что размерность климатического аттрактора выражается дробным числом, в полной мере объясняет внутреннюю изменчивость и непредсказуемость климата – как сравнительно недалекого прошлого, так и настоящего.

Разрушительным для классической небесной механики является утверждение великого русского математика В.И. Арнольда о существовании комет, поведение которых носит стохастический характер и определяется странным аттрактором, т.е. оно неустойчиво настолько, что их траекторию нельзя предсказать.

В конце главы стоит сделать обобщающий вывод. Стационарное состояние (подвижное равновесие, асимптотическая устойчивость) диссипативных систем подразумевает возможность притягивающего хаоса, когда в фазовом пространстве со временем любые траектории сходятся к некоторому аттрактору, причудливая форма которого и обуславливает хаотическую динамику. Появление хаоса в таких системах будет детерминировано, причем для этого может потребоваться всего несколько бифуркаций (бифуркация – резкая смена поведения системы при плавном изменении её параметров). Детерминированный хаос зафиксирован во многих природных системах, что появились веские основания считать это состояние доминирующем в Природе (Горяинов П.М., Иванюк Г.Ю.). Вообще, любой геологический процесс теперь можно описать на языке нелинейной динамики, если, например, ввести понятия циклического аттрактора для самоорганизации какого-то циклического процесса. Поэтому это огромное достижение синергетики. Но самое интересное, удалось понять, как система приходит к Хаосу…

Только по конечному состоянию системы нельзя установить её начальное состояние и большую часть траектории в фазовом пространстве (за исключением, быть может, самого последнего участка). Хаос «перемешивает» фазовое пространство, как Природа - геологическое «тесто».

«Не с такими ли системами, в которых две соседние (в настоящий момент) точки могут иметь совершенно разную историю, оставаясь в то же время в пределах одного аттрактора (образца породы, геологической структуры, блока, плиты, планеты Земля), - имеет дело геология?» (В.Н. Вадковский, В.С. Захаров).

V.2. Сценарии перехода к Хаосу

Пожалуй, не менее впечатляющим, чем само открытие детерминированного хаоса, стало открытие сценариев перехода к хаосу, от регулярной динамики к хаотичной.

V.2.1. Универсальность перехода к Хаосу по Файгенбауму

В 1976 году американский ученый Митчелл Файгенбаум сделал сенсационное открытие состоящие в том, что сценарий перехода к хаосу через бесконечный каскад бифуркаций удвоения периода универсален для большого числа динамических систем. Приобретение нового качества движения динамической системы при малом изменении параметров называется бифуркацией.

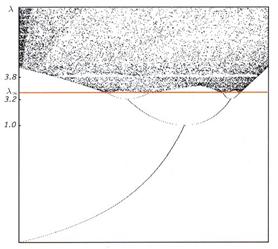
Между хаосом и порядком существует непосредственная связь: в процессе бифуркаций удвоения периода непериодический процесс возникает как предел все более сложных циклов, т.е. по сути, является сверхсложной организацией. Эпиграф данной работы: «Хаос – более высокая форма порядка». Кроме того, Файгенбаум получил константу, которую можно использовать для предсказания наступления хаоса (существует специальная формула).

В соответствии с этим сценарием ведут себя конвективные процессы при изменении параметров в подогреваемом слое жидкости, например в атмосферных процессах, и, вероятно, в мантии Земли. По предположению учёных, в ядре возможна турбулентная конвекция, возникающая по сценарию Файгенбаума.

V.2.2. Перемежаемость, обратный каскад

Переход от ламинарного течения к турбулентному часто проходит стадию специфического чередования этих режимов – перемежаемость (наоборот, обратный каскад).

В некоторых районах Земли исследователи сталкивались со сменой сейсмической активности странным образом. Длительный спокойный (ламинарный) режим прерывался резким хаотическим всплеском сейсмической активности, затем опять затишье и далее длительный интервал почти непрерывных хаотических колебаний сейсмической системы. Такое поведение может быть понято как проявление перехода к хаосу через перемежаемость ламинарного и турбулентного режимов.

Некоторые ученые в процессе складкообразования видят перемежаемость (смена «ламинарного» и «турбулентного режимов»).

Конечно, эти сценарии в реальных природных процессах выявить довольно сложно. Но относительно небольшое количество сценариев очень удивляет и внушает надежду. Это еще одна победа синергетики в попытке осознания реальности.

V.3. Самоорганизованная критичность

Совокупность взаимосвязанных, последовательно обуславливающих друг друга процессов, приводящих к разрушению одних и созданию других систем, представляет собой процесс самоорганизации надсистемы, объединяющей эти взаимодействующие системы. Характерными примерами самоорганизации являются подтопление территорий и развитие просадок в лёссах; сейсмические сотрясение и образование оползней, обвалов и лавин; растворение пород и образование карстовых провалов. Аналогичные процессы и участки среды получили название саморегулирующихся. Это происходит потому, что надсистема, возникшая из этих подсистем, соединила их в единый последовательный циклический процесс (циклический аттрактор), позволивший чутко реагировать на внешние воздействия. Внутри надсистемы происходят процессы разрушения и восстановления, но в целом её состояние устойчиво. Такой процесс называется самоорганизованной критичностью.

Наиболее простыми случаями для объяснения поведения сложных природных систем являются экстремальные состояния последних. Макроскопические свойства систем однородны в пространстве, что и позволяет достаточно легко их понять и описать.

Изучая реальные природные процессы, мы обычно имеем дело с одним или несколькими параметрами системы, изменяющимися во времени или в пространстве. Наиболее часто функция распределения какого-либо свойства реальной природной системы имеет степенной вид, а их спектр мощности - 1/f (f – частота) вид (вероятность событий в единицу времени обратно пропорциональна их силе). Степенной вид функции распределения указывает на то, что крупномасштабные события (катастрофические землетрясения, мощные вспышки на Солнце или образование месторождения-гиганта) случаются редко, но для их объяснения не нужно искать специальный механизм — он тот же самый, что и для менее крупномасштабных событий.

V.3.1. Модель "песчаной кучи"

В 1987 году П. Бак, Ч. Танг и К. Вайзенфельд для объяснения феномена шума типа 1/f (фликкер-шум) предложили теорию систем с самоорганизованной критичностью (СОК) — систем, которые без специального внешнего воздействия приходят в некоторое критическое состояние, поддерживаемое событиями разных масштабов.

То, как происходит переход в СОК-состояние и как оно динамически поддерживается, легко осмыслить, рассматривая простую и интуитивно понятную модель песчаной кучи, детально исследованную П. Баком и ставшую, по сути, символом теории самоорганизованной критичности. Кучка песка постоянно пополняется песчинками. При этом, когда наклон кучи становится критическим, усиливается сход песчаных лавин, а затем снова начинается процесс накопления и т.д. Когда сойдет всего несколько песчинок, или целая лавина, угадать нельзя. Такого рода сложные системы не только живут своей внутренней жизнью, но могут обладать высокой чувствительностью к внешним воздействиям, поскольку часть их элементов находится в предпороговом состоянии, когда достаточно небольшого толчка, чтобы накопленная энергия сбросилась. Когда этот слабый толчок происходит, множество предпороговых элементов высвобождают свою энергию одновременно, и энерговыделение в системе многократно превосходит обычное. Усиленное энерговыделение может стимулировать сброс энергии у элементов, более удаленных от порога, что лавинообразно увеличивает величину эффекта.

Лавинообразное энерговыделение происходит, если система до воздействия смогла "наполнить" свои резервуары, т.е. достаточно долго была без ощутимых внешних воздействий. При наличии же внешних достаточно сильных и частых воздействий сброс энергии элементами происходит далеко от порога, и коллективного высвобождения энергии, охватывающего всю систему или значительную ее часть, происходить не может. Это объясняет парадоксальное свойство систем такого типа: сильный отклик на слабые и редкие воздействия и малозаметный отклик на сильные и частые воздействия.

Эксперимент, проведенный группой венгерских ученых, показал существование СОК при формировании природных ландшафтов. Начальный "ландшафт" формировался медленным насыпанием мелкодисперсного кремнистого вещества на горизонтальную поверхность, что создавало миниатюрные "горные хребты". Для имитации водной эрозии поверхность "хребтов" увлажнялась с помощью пульверизатора. По мере насыщения водой часть материала начинала соскальзывать со склонов подобно лавинам или оползням в реальном мире, причем размер оползней опять имел степенное распределение. Распределение скоростей оползней также подчиняется степенному закону, но с другим показателем. Анализ геометрии контура склонов показал их фрактальность в широком интервале масштабов, подтверждая сделанное при компьютерном моделировании заключение, что фракталы могут генерироваться СОК-процессами (в общем смысле, фракталы можно рассматривать как мгновенные «срезы» самоорганизованных критических процессов) (по Горяинову П.М.).

С одной стороны профиль контура склона определяет место зарождения микро-оползня, скорость его движения, а также им охваченную площадь. Но ведь, с другой стороны, и сам профиль формируется многочисленными оползнями. В реальной природе процесс формирования глобального ландшафта имеет очень большую продолжительность во времени, поэтому имеющийся ландшафт может показаться чем-то постоянным, не изменяющимся. Может быть, поэтому, наблюдаемые катастрофические явления типа реальных оползней или лавин часто неудачно пытаются объяснить и предсказать, исходя из характеристик фиксированного ландшафта, искусственно разъединяя различные проявления одного динамического процесса. Это также касается сейсмических явлений: землетрясения — это не только события, происходящие в существующей структуре разломов, они сами эти разломы и формируют. Или, другими словами, землетрясения и существующая структура разломов — это различные проявления скрытого СОК-процесса. Проиллюстрируем явление самоорганизованной критичности несколькими природными примерами, так или иначе связанными с геологическими процессами.

V.3.2. Самоорганизованная критичность в геоморфологии

Оползни и лавины

В работе С. Хергартена и Х. Ю. Нёгебауера предложена модель формирования ландшафтов вследствие оползневых эффектов, которая учитывает устойчивость почвенных склонов и процессы переноса почвы, тектонические явления и образование аллювиальных отложений. Она также демонстрирует СОК-поведение, причем геометрические характеристики модельного ландшафта прекрасно согласуются с таковыми природных склонов, сформированных в результате воздействия оползней (Горяинов, Иванюк, 2001).

Речные сети

Как уже упоминалось, в лабораторных условиях боли получены результаты, говорящие о возможности формирования ландшафтов в результате СОК-феномена. Реальные ландшафты достаточно сложны и изменчивы, что указывает на комплексный характер их формирования. Удачным индикатором, характеризующим свойства ландшафта, являются речные системы.

Ветвление речных систем следует закону Хортона, который предложил сегментировать речную систему, присваивая начальному участку индекс 1, следующему сегменту, образующемуся при слиянии двух потоков — индекс 2, сегменту, возникающему при слиянии двух потоков с индексом 2 — индекс 3 и т. д. Закон Хортона гласит, что распределение сегментов отвечает степенному закону, и отношение числа сегментов с двумя соседними индексами, называемое бифуркационным отношением, приблизительно равно трем. Иерархическая структура притоков указывает на фрактальные свойства речных систем, а, следовательно, и ландшафтов в целом. Вычисляемая тем или иным способом фрактальная размерность топографических контуров является чувствительным показателем соотношения эндогенных и экзогенных

процессов в данном районе. Это заключение согласуется с разработками И. Родригес-Итурбе и А. Риналдо, которые численными методами моделировали эволюцию речных систем. Они также исходили из предположения, что формирование ландшафта происходит в результате взаимодействия двух процессов — воздымания земной поверхности в результате геодинамических явлений (внесения эндогенной энергии в систему) и водной эрозии (диссипация этой энергии). Эрозия начинается, когда воздействие водного потока на берега достигает критической величины. Последнее зависит от количества воды, протекающей через данную точку, и наклона поверхности в этой точке. Количество воды в каждой точке считается пропорциональным площади водосбора. Расчеты показали, что модельный ландшафт после многочисленных итераций переходит в стационарное состояние с фрактальной речной структурой и фрактальным ландшафтом, причем статистические характеристики полученных "компьютерных рек" близки к характеристикам реальных речных систем (Горяинов, Иванюк, 2001). Это позволило указанным авторам сделать вывод о том, что земная кора в результате самоорганизации переходит в критическое состояние, а это приводит к формированию "несбалансированных" ландшафтов.

V.3.3. Проявления СОК в эндогенных процессах

Землетрясения

По словам автора теории самоорганизованной критичности П. Бака, землетрясения являют собой, может быть, самый ясный и самый прямой пример СОК в природе. Согласно эмпирическому закону Гуттенберга-Рихтера:

logN=-bm+loga

где N — число землетрясений в единицу времени, m-магнитуда землетрясений,

b и а — константы (0.8 < b < 1.2, величина а определяется региональным уровнем сейсмичности). То есть, если мы наблюдали на определенной территории за определенный интервал времени 1000 землетрясений с магнитудой 4 балла по шкале Рихтера, то в том же пространственно-временном интервале произошло около 100 землетрясений с магнитудой 5 баллов и около 10 — с магнитудой 6 баллов. Степенная зависимость является первым указанием на то, что СОК может играть важную роль в динамике этого явления.

Подобно тому, как добавление песчинок вносит энергию в систему песчаной кучи, в сейсмическую систему непрерывно привносится эндогенная энергия, просачивающаяся по межблоковой перколяционной сети. Подземные толчки можно ассоциировать со скатыванием отдельных песчинок. Точно так же, как песчинки, взаимодействуя с соседними частицами, вызывают большие лавины (эффект домино), отдельный сейсмический толчок может спровоцировать толчки в соседних зонах, накопивших достаточно энергии. Эта цепная реакция и создает мощное разрушительное землетрясение в одном или нескольких узлах данного тектонического перколяционного кластера.

Исследователями были разработаны сложные модели, находящиеся в более полном соответствии с реально наблюдающимися процессами в зонах разломов, которые ко всему прочему продемонстрировали формирование фрактальной геометрии разломов.

Вулканизм

Группой итальянских ученых во главе с Диодати была исследована акустическая обстановка вблизи действующего вулкана. Временные зависимости мощности эмиссии выглядят как несвязанные шумоподобные сигналы, однако функция распределения числа всплесков эмиссии в течение одного часа одинакова для двух точек наблюдения и имеет привычный степенной вид с показателем около 1.5. По данным исследователя МакКлелланда с коллегами, объём тефры, выброшенной в ходе извержений, произошедших в период с 1975 по 1985 г., равно как в последние 200 лет вообще, соотносится с числом аналогичных по мощности извержений как степенная зависимость с показателем 2.14 (Горяинов, Иванюк, 2001). По-видимому, что и вулканическая активность также представляет собой СОК-явление. Косвенным подтверждением этому служит неоднократно упоминавшаяся в литературе фрактальная геометрия вулканических конусов, например, изображенной на рисунке Корякской Сопки на Камчатке.

V.3.4. Критические явления при осадкообразовании

Одним из наиболее вероятных механизмов образования флишевых толщ являются турбидитные потоки, время от времени сползающие по океаническому склону из-за постоянного поступления на него осадочного материала с континента.

В любом достаточно глубоком бассейне на определённой глубине уклон поверхности осадка неизбежно достигнет критической величины α, при которой откос станет неустойчивым и весь вновь поступающий материал будет оползать вниз по склону. Но, из-за наличия сил трения, ещё какое-то время накопление осадка будет продолжаться, - до тех пор пока его неустойчивая «сверхкритическая» верхняя часть не достигнет определённой массы. По той же причине, сорвавшись, неустойчивая часть осадка увлечет за собой в принципе устойчивые нижележащие слои. Возникающий турбидитный поток закладывает первый ритм флишевой толщи на дне бассейна, и процесс накопления осадка вновь будет продолжаться до достижения критического угла α.

Исследуя толщину слоев во флише, возможно оценить распределение мощности сформировавших его турбидитных потоков. В работе американского исследователя Ротмана приведены результаты измерения толщины 1235 слоев калифорнийских турбидитов. Толщины слоев хорошо описывается степенным законом с показателем 1.39 (т.е структура самоподобна, фрактальна), что подтверждает применимость теории самоорганизованной критичности и к этому природному явлению (Горяинов, Иванюк, 2001).

Итак, можно сделать вывод, что самые разные геологические процессы (осадкообразование, формирование ландшафта, сейсмическая и вулканическая активность) на разных временных и пространственных масштабах проявляют динамику, свойственную системам в состоянии самоорганизованной критичности. В модели песчаной кучи не акцентировалось внимание, откуда появляются песчинки или какой механизм обеспечивает их исчезновение из системы. Наблюдая природные явления, можно предположить тесное взаимодействие СОК-процессов. Землетрясения должны играть важную роль при формировании турбидитов. Во время землетрясения в Спитаке в 1988 году река мгновенно, с точки зрения времени формирования ландшафта, проложила новое русло в сотнях метров от старого. Модель формирования ландшафта оползнями демонстрирует степенную зависимость сброса грунта в речную сеть, что должно служить источником для новой СОК-системы. Совокупность этих фактов делает перспективным рассмотрение земной коры как единой СОК-системы, критичность которой проявляется в ее фрактальной структуре и в динамике процессов, в ней протекающих.

В конце стоит ещё раз отметить на парадоксальное свойство СОК-систем: сильный отклик на слабые и редкие воздействия и малозаметный отклик на сильные и частые воздействия.

Поэтому в рамках этой теории лучше объясняется влияние космических факторов на земные процессы, в частности, фазы Луны на мелкофокусные землетрясения (по Н.В. Короновскому) и т.п.

Это была попытка кратко изложить основы теории самоорганизованной критичности, отметить возможные области ее применения.

Глава VI. Немного о вопросе самоорганизации тектоносферы

Главным выводом данной работы должно стать признание самоорганизации тектоносферы (тектоносфера - главная внешняя область проявления тектонических и магматических процессов Земли, охватывающая земную кору и часть верхней мантии (включая астеносферу) до глубин около 700 км).

«В целом Земля является самоорганизующейся системой, геосферы которой образовались за счет диссипативных процессов» (Ф.А. Летников). Это требует принципиально нового подхода к построению тектонической концепций, которые обязаны учитывать наличие дальнего порядка в строении литосферных блоков в широчайшем масштабном диапазоне: от литосферы в целом до отдельных минеральных зерен и даже атомных кластеров. Образование любой макроформы (структуры) является следствием «кооперативного взаимодействия микрочастей, вплоть до молекул» (И. Пригожин), т.е. присутствует согласованность взаимодействия частей при образовании структуры как единого целого. Такая особенность структурной организации предусматривает полный отказ от идеи автономного (несогласованного) перемещения тектонических макроблоков относительно друг друга как физически некорректной. Устойчивость (гомеостазис) тектоносферного структурного макроузора при непрерывно активной динамике на нижележащих иерархически соподчиненных уровнях - это и составляет главный физический смысл геологической самоорганизации – постоянного усложнения, упорядочения, дифференциации в структурах тектоносферы.

Разные авторы ставят различные акценты в вопросе самоорганизации. Например, Горяинов П.М. и Иванюк Г.Ю. построили полноценную концепцию самоорганизации тектоносферы, причиной которой является перколяция эндогенной энергии.

В задачи данной работы входит лишь утвердить положение о самоорганизации как основное для дальнейших разработок.

Заключение

Жизнь показала, что законы Природы являются гибкими, а не строгими. Природа и структура Вселенной находится в процессе постоянного изменения. Теория Хаоса позволяет сконцентрироваться на процессе, в то время как классическая физика концентрировалась в основном на его содержании.

На современном этапе геология, как и другие области знания, накопила огромный арсенал понятий и терминов. Одна из глобальных целей синергетики как призыв «единая наука о единой Природе» является универсальное описание любого процесса. Может быть, исходя из этой концепции, принцип Оккамы уже должен трактоваться как отказ от излишней «линейности», приводящей описание по определению нелинейных процессов к нагромождению слов, уводящих от истины. Нелинейность не разрушает всю предыдущую теорию, она просто идёт дальше, открывает новые горизонты познания, но и новые возможности, методы.

Конечно, концепция нелинейности – всего лишь новое приближение. В Природе нет ни линейности, ни нелинейности. Просто философия синергетики (теории Хаоса, науки о сложности и т.п.) очень глубока, и есть надежда, что её тропинка ведёт к пониманию Сути вещей, и мы делаем по ней первые шаги.

Синергетическое мировоззрение существовало всегда (вспомним хотя бы Гераклита, даосов). Но исторически наша цивилизация начала её принимать, уже «находясь в крайне неравновесном состоянии» (по Князевой Е.Н и др.). Встала необходимость переосмысления роли геологической разведки полезных ископаемых в жизни нашего общества. Нескончаемая добыча без привнесения нового неприемлема. Природа уже находится в крайне неравновесном состоянии и начала давать о себе знать участившимися катаклизмами («сходами лавин»). Поэтому необходимо направить усилия на поиск альтернативных источников энергии. Нужно построить наши взаимоотношения с Природой как коэволюцию сложных систем - базовый принцип «Нового диалога Человека с Природой». «Коэволюция различных систем означает трансформацию всех подсистем посредством механизмов установления когерентной связи и взаимного согласования параметров их эволюции» (Князева Е.Н., Курдюмов С.П.).

С этой точки зрения интересно направление в строительстве – архитектурная бионика. На основе исследований ученых о взаимоотношениях живой и неживой Природы, делаются попытки привнести всю мудрость устройства некоторых живых организмов в архитектурное строительство.

Прогноз и управление рисками как прикладное направление теории Хаоса бурно развивается в наше время. Оказалось, что при математическом моделировании объектов, связанных с возможностью кризисных ситуаций есть области, в которых горизонт прогноза резко сокращается и которые связаны с большим риском. Они были названы областями джокеров. Сам джокер – это правило, в соответствии с которым объект в фазовом пространстве может совершить скачок. Выделение областей джокеров и их анализ в природных и техногенных системах является важным направлением усилий ученых. Оказалось, что наряду с областями джокеров, где прогнозировать трудно, в фазовом пространстве существуют русла, где ход процессов предопределен, и сложные объекты можно описывать достаточно просто. Есть основания полагать, что умение быстро искать русла, будет очень удобным средством прогнозирования. Эти разработки очень важны для инженерной геологии, да и вообще для науки в целом.

В данной работе были рассмотрены базовые понятия и некоторые идеи применения синергетики в геологии. Перспективность синергетики требует внедрения синергетических принципов геологических исследований.

Усовершенствование принципа актуализма в связи с осознанием большой роли бифуркационного процесса в ходе эволюции:

Понятие катастрофистов «чудо» - оно же случай – определяет выбор системой пути развития в устойчивое состояние в точке катастрофы (бифуркации), где происходит ветвление эволюционных путей. Их может быть много, даже бесконечно много. В точках бифуркации Природа как бы раскрывает свои потенциальные возможности, а неизбежно присутствующая случайность выбирает тот единственный канал, по которому дальше и будет развиваться система. Бифуркационный механизм играет важнейшую роль в общей эволюционной схеме. По существу, именно он является источником роста разнообразия различных форм организации материи, а, следовательно, и непрерывно возрастающей сложности её организации. После бифуркации наступит некоторый новый спокойный участок «дарвиновского» развития, который может смениться новой бифуркацией. Таким образом, теория самоорганизации делает следующий шаг на том пути постепенного понимания мирового эволюционного процесса, по которому шли Кювье, Ламарк, Дарвин.

Не только спокойная постепенная эволюция, но и неизбежные катастрофы с их качественно новыми непредсказуемыми последствиями – вот каков облик нашего изменяющегося Мира. Подобное уже писал Виктор Ефимович Хаин. Катастрофы и плавное развитие порождаются одними и теми же системами.

Приведем самое смелое предположение современного абстрактного геологического знания, напрямую вытекающее из теории самоорганизации. Подразумевается, что в основе изменений объектов направленных в сторону их усложнения лежат процессы аналогичные тем, которые происходят с живыми объектами, то есть подразумевается некоторое активное отношение, сродни познавательному, и которое позволяет элементам систем организовываться с таким результатом, который предполагает достижение нового состояния, обеспечивающего благоприятное положение относительно других объектов и сохранения собственной целостности. Но такое положение возможно занять только используя знание «рельефа местности», то есть тех законов, которыми образован сам объект. Более того, можно предположить, что «суть этой самоорганизующейся формы существования составляет именно практико-познавательная деятельность по аналогии с деятельностью разумных существ» (Крылов И.М.). Вспомним теорию ГЕИ – Живой Земли…

На смену редукционистскому подходу Аристотеля приходит принцип выделения в целом определенных параметров порядка, определяющих её поведение (философия Гераклита). Как можно понять из данной работы, синергетика показала, что в нашем мире есть довольно немного качественно разных типов поведения, для их описания был разработан универсальный аппарат; было отмечено сходство механизмов протекания многих процессов; появляются новые идеи в попытках прогноза. Из этого утверждения можно сделать вывод, исследования в этой области знаний на верном пути…

Литература:

1. Вадковский В.Н., Захаров В.С., электронное учебное пособие «Динамические процессы в геологии: первое знакомство с нелинейными системами», 2001
2. Горяинов П.М., Иванюк Г.Ю. Самоорганизация минеральных систем. Синергетические принципы геологических исследований. Москва, ГЕОС, 2001.
3. Иванов О.П., Малинецкий Г.Г., Рагозин А.Л. Синергетика природных опасностей и рисков. // Труды семинара «Синергетика». Т. 4, М., МГУ, 2001.
4. Князева Е.Н., Курдюмов С.П. Особенности неравновесных процессов в открытых диссипативных средах. // «Проблемы геофизики XXI века». Т.1, Москва, Наука, 2003
5. Короновский Н.В. Общая геология. Москва, МГУ, 2002
6. Кравченко Н.С., «Принцип Кюри как регулирующий механизм эволюции в бифуркационных процессах (на примере геологических систем)», 1998. http://ihtik.lib.ru/philosarticles_22apr2005/philosarticles_22apr2005_4664.rar
7. Крылов И.М. «Синергетика как этап становления научной философии», 2003. http://sciteclibrary.ru
8. Летников Ф.А. Синергетика геологических систем. Новосибирск, Наука, 1992.
9. Малинецкий Г.Г., «Новый облик нелинейной динамики», Москва, «Знание – сила», №3, 2005, стр. 38 - 45
10. Мандельброт Б. Фрактальная геометрия Природы. Москва-Ижевск, ИКИ, 2002
11. Наймарк А.А., «Фрактальность геологической среды и проблема прогнозируемости сейсмогенного макроскалывания», Известия ВУЗов, Геология и разведка, 1997, №2, с.23-31
12. Пригожин И.Р., Стенгерс И. Порядок из Хаоса: Новый диалог человека с Природой. Москва, УРСС, 2005
13. Тимашев С.Ф. О базовых принципах «Нового диалога с Природой». // «Проблемы геофизики XXI века». Т.1, Москва, Наука, 2003
14. Тихоплав В.Ю., Тихоплав Т.С. Гармония Хаоса или Фрактальная реальность. Санкт-Петербург, Весь, 2003.
15. Трубецков Д.И. Введение в синергетику: Хаос и структуры. Москва, УРСС, 2004
16. Хакен Г. Синергетика. Москва, Мир, 1991
17. Шипов Г.И. Теория физического вакуума. Москва, НТ-центр, 1993
18. Якушова А.Ф., Хаин В.Е., Славин В.И. Общая геология. Москва, МГУ, 1988
19. Сборник «Архитектурная бионика», Москва, Стройиздат, 1990.
20. Turcotte D.L. “Fractals and chaos in geology and geophysics”. Cambridge University Press, Cambridge, 1997
21. Sammis C.G., Osborne R., Anderson J.L., Banerdt M., White P. Self-similar cataclasis in the formation fault gauge. // PAGEOPH. 1986. Vol. 124, p. 53-78 (по [2])

2006

Электронная библиотека портала GEODYNAMICA.RU