Моделирование фазовых равновесий при кристаллизации базальтовых магм
Назад | Оглавление|
Далее
Предложенные в предыдущих разделах
алгоритм моделирования кристаллизации
многофазных систем (Рис. 2.1,
2.2) и автоматизированная база
данных по расплавно-минеральным равновесиям (ИНФОРЭКС-4.0) составляют
термодинамическую и эмпирическую основу для
построения реалистичных моделей фазовых
равновесий кристаллизующихся магм. На пути
построения такого рода моделей мы прошли
последовательно путь от анализа упрощенных
силикатных систем (модель РТФК - Арискин, 1985) и
использования простейших геотермометров
минерал-расплав (Roeder,
Emslie, 1970; Longhi et al., 1978; Drake, 1976b; Nielsen,
Drake, 1979) к более сложным силикатным системам и
моделям, позволяющим учесть эффект неидеального
поведения расплава, влияние давления и воды на
фазовые равновесия, кристаллизацию железорудных
минералов в зависимости от редокс-условий.
Важным результатом многолетних
расчетов, анализа и тестирования этих моделей
явился вывод о необходимости калибровок
уравнений равновесия минерал-расплав в
диапазоне составов близком составам пород, в
изучении которых заинтересован исследователь.
Это сознательное ограничение экспериментальной
выборки для калибровки ЭВМ-моделей позволяет при
их использовании достичь максимальной точности
вычислений и в итоге повысить значимость
генетической интерпретации изверженных
пород. Предложенный нами подход с практической
точки зрения отличается от подхода к
моделированию магматических равновесий,
развиваемому Гиорсоу с коллегами,
которые еще в середине 80-х годов провозгласили
построение "суперсистемы" MELTS,
ориентированной на максимально широкий диапазон
составов и условий кристаллизации магматических
расплавов (Ghiorso et al.,
1983; Ghiorso, 1985). Впрочем, теперь эти авторы
признают, что проблемы термодинамической
обработки и качество многих экспериментальных
данных не позволяют надеяться, что задача
построения "суперсистемы моделирования магм"
может быть решена в ближайшие годы (Ghiorso, 1997).
В последующих разделах будут
рассмотрены эмпирические уравнения и
зависимости, составлящие основу ЭВМ-модели КОМАГМАТ,
разработанной для решения задач, связанных с
дифференциацией толеитовых и известково-щелочных магм (Ariskin et al., 1993).
Редокс-равновесие
Fe3+/Fe2+ в магматических расплавах
Оксиды железа FeO и Fe2O3
относятся к важнейшим компонентам силикатного
расплава, от соотношения которых зависят
физические свойства магматических жидкостей ( Dingwell, 1991; Kress, Carmichael,
1989; Toplis et al., 1994b), составы
кристаллизующихся фемических
силикатов, условия появления на ликвидусе
железорудных минералов (Hill, Roeder, 1974; Nielsen et
al., 1994; Toplis, Carroll, 1995; Ariskin, Nikolaev, 1996) и в
конечном счете - направленность
фракционирования базальтовых магм (Osborn, 1959; Presnall,
1966; Бабанский и др.,
1983; Ghiorso, Carmichael,
1985; Кадик и др.,
1986, 1990; Арискин и др., 1987, 1988; Toplis, Carroll, 1996).
С термодинамических позиций принято
различать два главных режима поведения FeO и Fe2O3
в кристаллизационном процессе. В условиях закрытой системы изменение
соотношений этих компонентов контролируется
железистостью фемических силикатов, пропорциями
и составом выделяющихся железорудных фаз (магнетит, ильменит).
Кристаллизация оливина и пироксенов
приводит к удалению части закисного железа из
силикатной жидкости, относительному накоплению
Fe2O3 и повышению общей степени
окисления железа в расплаве FEox=Fe3+/(Fe3+
+ Fe2+). Выделение магнетита имеет обратный
эффект, поскольку удаление Fe2O3 и FeO в
отношении примерно 1:1 приводит к быстрому
понижению "степени окисленности" силикатной
жидкости (Ghiorso,
Carmichael, 1985; Арискин
и др., 1987; Toplis,
Carroll, 1996).
При кристаллизации в условиях
системы открытой или буферированной по
давлению кислорода соотношения трех- и
двухвалентного железа в расплаве определяются окислительно-восстановительными
реакциями:
FeO (l)+1/4O2=1/2Fe2O3 (l)(2.26а)
или
FeO (l)+1/4O2=1/2FeO1.5 (l),(2.26б)
в зависимости от выбранных
компонентов расплава. Реакция (2.26б) "удобна" в
том смысле, что ее термодинамический анализ
позволяет определить природу зависимости
отношения Fe3+/Fe2+ в расплаве от
интенсивных параметров. Константа
равновесия реакции (2.26б)
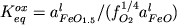 , (2.27) , (2.27)
где 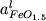 и и 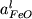 активности окиси
и закиси железа в расплаве. Учитывая зависимости
активностей от концентрации ( активности окиси
и закиси железа в расплаве. Учитывая зависимости
активностей от концентрации ( 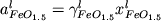 и и 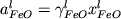 ),
выражение (2.27) преобразуется в уравнение ),
выражение (2.27) преобразуется в уравнение
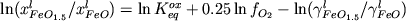 .(2.28) .(2.28)
В общем случае, величина 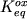 зависит от энтальпии и энтропийного
эффекта реакции (2.26б):
зависит от энтальпии и энтропийного
эффекта реакции (2.26б):
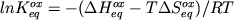 ,(2.29) ,(2.29)
так что теоретически отношение Fe3+/Fe2+(2.28) можно было бы
рассчитывать, исходя из термодинамических
свойств оксидов железа в расплаве и заданной летучести кислорода. В
действительности, значения коэффициентов
активности FeO и FeO1.5 (или Fe2O3) в
расплаве неизвестны, поэтому для оценки
отношения разновалентных форм Fe(III) и Fe(II)
используются эмпирические зависимости вида
![\begin{displaymath}\ln [ Fe (III) / Fe (II)] = a \ln f_{O_2} + b / T + c + \sum_{i=1}^n d_i x_i^l \end{displaymath}](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula8.gif) ,(2.30) ,(2.30)
где a, b и 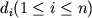 -
регрессионные коэффициенты, а отношение -
регрессионные коэффициенты, а отношение 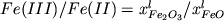 ; (Sack
et al., 1980; Kilink et al., 1983; Борисов, Шапкин, 1989;
Kress, Carmichael, 1989, 1991;
Moore et al., 1995; Baker, Rutherford, 1996; Righter, Carmichael, 1996)
или ; (Sack
et al., 1980; Kilink et al., 1983; Борисов, Шапкин, 1989;
Kress, Carmichael, 1989, 1991;
Moore et al., 1995; Baker, Rutherford, 1996; Righter, Carmichael, 1996)
или 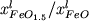 (Mysen,
1991; Николаев
и др., 1996). (Mysen,
1991; Николаев
и др., 1996).
Уравнения (2.30)
калибруются по результатам специальных
редокс-экспериментов, которые включают выдержку
исходных материалов при температурах выше
ликвидусной и заданной летучести кислорода, с
последующим анализом закалочных
стекол на истинное содержание закиси железа FeO.
Это позволяет оценить содержание окисленной
формы железа в расплаве по разности Fe2O3=1.1113*(FeOобщ-FeO).
Из сопоставления уравнений (2.26-2.30) ясно, что в идеальном
случае коэффициент a равен 0.25, величина b
должна быть соразмерна энтальпии
реакции 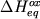 , а сумма , а сумма 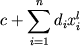 учитывает эффект
изменения энтропии учитывает эффект
изменения энтропии 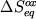 и
влияния состава. и
влияния состава.
Сэк с коллегами (Sack et al., 1980)
провели серию из 57 "сухих" экспериментов по
изучению степени окисления железа в природных
расплавах и обработали их при помощи уравнения (2.30) совместно с данными 86
редокс-экспериментов, проведенных при
атмосферном давлении другими исследователями (Kennedy, 1948; Fudali,
1965; Shibata, 1967; Thornbern, 1980). В результате была
получена эмпирическая зависимость, параметры
которой приведены в Табл. 2.3.
Несколько лет спустя базовая выборка для
калибровки была расширена за счет
дополнительных опытов, проведенных на воздухе (Kilink et al., 1983).
Уравнение Килинка (см. параметры в Табл. 2.3) пользуется наибольшей
популярностью среди зарубежных специалистов в
области ЭВМ-моделирования фазовых равновесий и
обычно является критерием точности при анализе
новых результатов редокс-экспериментов (Moore et al., 1995; Baker,
Rutherford, 1996; Righter, Carmichael, 1996). Последующие
попытки пересмотра формы уравнения (2.30) и включение новых
экспериментальных данных не привели к повышению
его точности: погрешности оценки содержания
оксидов железа стабильно варьировали около 0.2
мас.% для FeO и 0.3-0.4 мас.% для Fe2O3 (Kress, Carmichael, 1989, 1991).
Таблица 2.3.
Регрессионные коэффициенты к уравнениям вида (2.30), полученным разными
авторами за период 1980-1996 гг.
Ссылка |
Sack et al., 1980 |
Kilink et al., 1983 |
Kress, Carmichael, 1991 |
Николаев и др., 1996:
(толеитовые серии, |
| |
(n=143) |
(n=186) |
(n=228) |
(n=56) |
Логарифм окисленности |
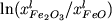
|
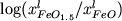
|
a(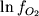 ) ) |
0.2181 |
0.2185 |
0.196 |
0.1395 1 |
b(1/T) |
13185 |
12670 |
11492 |
3282.2 |
c |
-4.4993 |
-7.54 |
-6.675 |
- |
dSiO2 |
-2.1504 |
- |
- |
-1.4238 |
dTiO2 |
- |
- |
- |
-4.3585 |
dAl2O3 |
-8.3516 |
-2.24 |
-2.243 |
-9.4488 |
dFeO(общ) |
-4.4951 |
1.55 |
-1.828 |
-0.7550 |
dMgO |
-5.4364 |
- |
- |
-2.2326 |
dCaO |
0.0731 |
2.96 |
3.201 |
0.3404 |
dNa2O |
3.5415 |
8.42 |
5.854 |
2.4766 |
dK2O |
4.1869 |
9.59 |
6.215 |
4.4534 |
dP2O5 |
- |
~ (-6) 2 |
- |
- |
dOH_ |
- |
~ (+8.8) 3 |
- |
- |
Давление |
- |
- |
Учитывается 4 |
- |
Примечания. 1В уравнениях Николаева и др. (1996) в
качестве параметра регрессии использовались
десятичные логарифмы 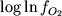 . 2Оценка
влияния фосфора дана по результатам (Toplis et al., 1994b).
3Влияние воды оценено по данным (Baker, Rutherford, 1996)
для систем риолитового состава. 4Фактор
давления откалиброван на основании данных о
сжимамости и теплоемкости оксидов железа в
расплаве. . 2Оценка
влияния фосфора дана по результатам (Toplis et al., 1994b).
3Влияние воды оценено по данным (Baker, Rutherford, 1996)
для систем риолитового состава. 4Фактор
давления откалиброван на основании данных о
сжимамости и теплоемкости оксидов железа в
расплаве.
При анализе данных о
редокс-равновесиях в расплавах Борисов (1988) обратил
внимание на то, что эмпирические коэффициенты b
при обратной температуре не постоянны (2.30) и для разных составов
колеблются в широком интервале, примерно от -2000
до 10000. Это поставило под сомнение возможность
адекватного описания отношений Fe2O3/
FeO или Fe3+/Fe2+ для всех классов магматических пород с помощью
уравнений, включающих постоянные значения
коэффициента b. Для учета этого фактора было
предложено новое уравнение, где параметры a и b
также являлись функцией состава расплава (Борисов, Шапкин, 1989).
Калибровка параметров этого уравнения была
проведена на базе данных (Kilink et al., 1983), а
данные сравнений с моделью Килинка указывали на
небольшое, но систематическое повышение
точности при использовании уравнения
Борисова-Шапкина для решения обратных задач.
Другой путь решения этой проблемы
предложил Майсен, который представил
эмпирическое уравнение, включающее в качестве
независимых переменных 6 химических параметров
расплава (Al/Al+Si, Fe3+/Fe3++Si и некоторые
другие), основанных на представлениях автора о
структурном состоянии силикатной жидкости (Mysen, 1991).
Применение этого уравнения осложняется
необходимостью построения итерационного цикла,
учитывающего, что концентрации окисного и
закисного железа входят одновременно и в правую
и в левую часть уравнения редокс-равновесия.
Тестирование уравнения Майсена показало, что,
несмотря на оптимистичные заявления этого
автора, оно не дает повышения точности расчетов
по сравнению с другими моделями (Николаев и др., 1996).
Альтернативный подход к повышению
точности редокс-вычислений может быть связан с
введением дополнительных ограничений на условия
калибровки по составу закалочных
стекол и диапазону летучести
кислорода. Для решения этой задачи мы
использовали информацию из базы данных ИНФОРЭКС-3.0
(Ariskin et al., 1996).
Из данных 298 редокс-экспериментов были отброшены
результаты, полученные в простых синтетических
системах и в наиболее окислительных условиях logfO2>NNO+1.
Полученная выборка составов (всего 170) была
разделена на четыре серии: условно "толеитовую"
(n=56), "субщелочную" (n=50); "щелочную"
(n=50) и "андезит-риолитовую" (n=14),
каждая из которых обрабатывалась раздельно по
линейной модели типа (2.30).
Параметры соответствующей
эмпирической зависимости для расплавов толеитовой серии приведены в Табл. 2.3. Точность решения
обратной задачи для отношения Fe3+/Fe2+
при использовании этих коэффициентов составляет
в среднем  0.029 (Николаев
и др., 1996), что практически не отличается от модели Борисова-Шапкина ( 0.029 (Николаев
и др., 1996), что практически не отличается от модели Борисова-Шапкина (  0.032) и
незначительно превышает среднюю точность
уравнений (Sack et al.,
1980; Kilink et al., 1983; Kress, Carmichael, 1989, 1991; Mysen, 1991),
которая составляет 0.032) и
незначительно превышает среднюю точность
уравнений (Sack et al.,
1980; Kilink et al., 1983; Kress, Carmichael, 1989, 1991; Mysen, 1991),
которая составляет  (0.035-0.036). (0.035-0.036).
Таким образом, приходится признать,
что на сегодняшний день не существует подхода,
который позволил бы принципиальным образом
повысить точность редокс-вычислений для
определения отношения Fe3+/Fe2+ в
расплавах. По-видимому, средние погрешности (Fe3+/Fe2+)эксп-(Fe3+/Fe2+)расч
имеют порядок  0.03 - максимум, которого можно
достичь при согласовании данных, полученных в
разных лабораториях (Николаев
и др., 1996). Эту ситуацию иллюстрирует Рис. 2.15, где экспериментальные
данные по отношениям Fe3+/Fe2+ в толеитовых и андезитовых
расплавах сопоставляются с результатами
расчетов по моделям Борисова-Шапкина
и Сэка. 0.03 - максимум, которого можно
достичь при согласовании данных, полученных в
разных лабораториях (Николаев
и др., 1996). Эту ситуацию иллюстрирует Рис. 2.15, где экспериментальные
данные по отношениям Fe3+/Fe2+ в толеитовых и андезитовых
расплавах сопоставляются с результатами
расчетов по моделям Борисова-Шапкина
и Сэка.
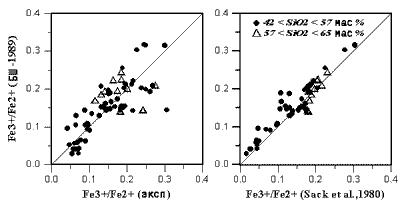 |
Рис. 2.15.
Сравнение экспериментальных и
расчетных значений отношения Fe3+/Fe2+ в
расплавах "толеитовых" систем и андезитов
при летучести кислорода ниже NNO+1
Данные о редокс-равновесиях из
системы ИНФОРЭКС-4.0
(Арискин и др., 1997):
толеитовых базальтов - 55, андезитов - 11.
Левый график показывает воспроизводимость
экспериментальных
значений при использовании уравнения (Борисов, Шапкин, 1989);
на правом графике сопоставляются результаты
вычислений
по моделям Борисова-Шапкина и Сэка. |
Влияние других интенсивных параметров.
Результаты (Toplis et al.,
1994b) показывают, что увеличение содержания P2O5
приводит к восстановлению части окисного железа,
которое по масштабам сравнимо с влиянием
щелочных компонентов и усиливается при переходе
к более восстановительным условиям (Табл. 2.3). Эффект
присутствия воды специально исследовался
в работах (Moore et al.,
1995; Baker, Rutherford, 1996). Несколько неожиданным
явился вывод о слабом влиянии H2O на
редокс-равновесия с участием железа: для
большинства опытов было установлено
соответствие экспериментально установленной и
рассчитанной по уравнению Килинка окисленности
расплава. Приведенный в Табл. 2.3
высокий коэффициент при гидроксильном
компоненте относится только к системам риолитового
состава (Baker, Rutherford,
1996). Влияние давления было оценено из
данных о сжимаемости и теплоемкости FeO и Fe2O3
в расплаве (Kress,
Carmichael, 1991). Эти авторы отмечают, что объемный
эффект реакции окисления (2.26)
остается положительным до давлений порядка 30
кбар: это означает, что при постоянной
температуре и летучести кислорода отношение Fe3+/Fe2+
слабо понижается с ростом давления. При
практических расчетах этот эффект пренебрежимо
мал.
В большинстве программ серии КОМАГМАТ
мы используем уравнение (2.30)
с параметрами Сэка (Табл. 2.3);
новейшие версии типа модели МЕТЕОМОД
(Ariskin et al., 1997)
включают возможность варьирования
регрессионных коэффициентов и использование
уравнений (Kilink et
al., 1983; Борисов,
Шапкин, 1989; Kress,
Carmichael, 1991). Последующие расчеты показали, что
небольшие различия точности этих уравнений
практически не сказываются на температурах и
составах кристаллизующихся силикатов. Для
моделирования появления железорудных
минералов погрешности оценок содержания FeO и Fe2O3
во всех случаях оказываются велики, что требует
особой методики калибровок для магнетита и
ильменита (см. ниже).
Представляется важным и тот факт, что
предложенный в разделе 2.1 метод минимизации термодинамического
потенциала допускает открытость системы по
кислороду и совместное решение уравнений
равновесия для реакций окисления (2.26) и кристаллизации
минералов. Это не требует принципиального
изменения алгоритмов, представленных на Рис. 2.1 и
2.2.
При расчетах закрытых систем
уравнение (2.30)
преобразуется в зависимость logfO2 от
температуры и степени окисления расплава.
Точность расчета logfO2 составляет при
этом 0.5-0.7 лог.ед .
Начало систематическим исследованиям
распределения элементов между минералами и
базальтовым расплавом положила известная
экспериментальная работа (Roeder,
Emslie, 1970). Эти авторы провели 27 экспериментов
по плавлению оливиновых и щелочных
базальтов Гавайских о-вов и показали, что в
диапазоне температур 1150-1300°С и летучести
кислорода -12 < logfO2 < -0.7 зависимость
логарифмов молекулярных коэффициентов
распределения MgO и FeO между оливином
и расплавом от обратной температуры носит
линейный характер (Табл.
1.1) - Рис. 2.16. Коэффициенты
корреляции 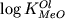 от 1/T оказались
довольно высоки: r=0.965 для MgO и r=0.880 для FeO.
Это указывало, что установленные эмпирические
закономерности могут быть использованы для
целей термометрии условий
образования магматических пород,
содержащих оливин. Последующие
результаты тестирования этих уравнений на
независимых экспериментальных данных показали,
что при известном составе оливина и расплава их
использование дает оценки температур с
точностью порядка 20оС. от 1/T оказались
довольно высоки: r=0.965 для MgO и r=0.880 для FeO.
Это указывало, что установленные эмпирические
закономерности могут быть использованы для
целей термометрии условий
образования магматических пород,
содержащих оливин. Последующие
результаты тестирования этих уравнений на
независимых экспериментальных данных показали,
что при известном составе оливина и расплава их
использование дает оценки температур с
точностью порядка 20оС.
Позднее было проведено 19
дополнительных экспериментов в условиях низкой
фугитивности кислорода logfO2 < -12 на
базальтах из других регионов (Roeder, 1974).
Обработка полученных данных совместно с
результатами (Roeder,
Emslie, 1970) подтвердила установленные ранее
закономерности (Рис. 2.16). При этом наблюдалось
заметное увеличение разброса экспериментальных
точек относительно регрессионных линий.
Эти работы Редера по времени совпали с
началом интенсивного изучения лунного вещества,
в частности, экспериментальных исследований
фазовых равновесий лунных базальтов.
В результате опытов с образцами низкотитанистых
и высокотитанистых морских базальтов
в сильно восстановительных условиях были также
установлены линейные зависимости 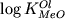 от 1/T
(Longhi et al., 1978),
однако рассчитанные регрессионные линии были
смещены относительно данных (Roeder, Emslie, 1970; Roeder,
1974) - Рис. 2.16. от 1/T
(Longhi et al., 1978),
однако рассчитанные регрессионные линии были
смещены относительно данных (Roeder, Emslie, 1970; Roeder,
1974) - Рис. 2.16.
Термодинамическое рассмотрение этого
вопроса указывало на сильную зависимость
коэффициентов распределения Ol-расплав от
состава, прежде всего от активности SiO2 в
жидкости (Longhi et
al., 1978), см. уравнения (1.20-1.24). Лонги исследовал
несколько моделей геотермометров и
пришел к выводу, что включение концентрационных (
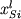 ) или структурно-химических параметров (2Si/O,
Si/(Si+Al) и др.), в уравнения равновесия вида (1.22,
1.24) позволяет
рассчитывать сложные коэффициенты
распределения ) или структурно-химических параметров (2Si/O,
Si/(Si+Al) и др.), в уравнения равновесия вида (1.22,
1.24) позволяет
рассчитывать сложные коэффициенты
распределения 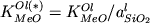 , для
которых линейная зависимость , для
которых линейная зависимость 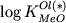 от 1/T
характеризуется более высокими коэффициентами
корреляции. Улучшение наблюдалось как для земных
(Roeder, 1974), так и
для лунных (Longhi et al.,
1978) оливиновых геотермометров. При
этом сдвиг между регрессионными линиями на
диаграммах типа Рис. 2.16 для
одного и того же компонента (MgO или FeO) несколько
уменьшился, но оставался значимо различим для
данных экспериментов на земных и лунных
составах. от 1/T
характеризуется более высокими коэффициентами
корреляции. Улучшение наблюдалось как для земных
(Roeder, 1974), так и
для лунных (Longhi et al.,
1978) оливиновых геотермометров. При
этом сдвиг между регрессионными линиями на
диаграммах типа Рис. 2.16 для
одного и того же компонента (MgO или FeO) несколько
уменьшился, но оставался значимо различим для
данных экспериментов на земных и лунных
составах.
Объснение этого факта связано со
спецификой составов лунных базальтов,
которые систематически обогащены FeO и обеднены
щелочами по сравнению с земными базальтоидами.
Этому выводу были созвучны результаты анализа,
проведенного на простых синтетических системах:
для согласованного описания поверхности оливинового ликвидуса на различных
фазовых диаграммах необходимо допускать сильную
зависимость активности Fo и Fa от
нормативного содержания альбита или нефелина (Перчук,
Ваганов, 1978). Вопрос о влиянии
кремнекислотности и щелочности на коэффициенты
распределения получил развитие в работе (Drake, 1976), где
равновесие Pl-расплав было исследовано
экспериментально и теоретически.
Дрейк провел 55 опытов на синтетических
составах от "базальтов" до "риолитов" при атмосферном давлении, в
диапазоне температур 1095-1400°С. Фугитивность
кислорода не контролировалась, а
продолжительность плавок составляла не менее
недели, что позволяло получать довольно
однородные по составу кристаллы (  3 мол.% An).
На первом этапе термодинамической обработки
данных этих экспериментов были рассчитаны
простые весовые коэффициенты распределения 3 мол.% An).
На первом этапе термодинамической обработки
данных этих экспериментов были рассчитаны
простые весовые коэффициенты распределения 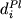 (i=Na,Ca,Al,Si) и зависимости
(i=Na,Ca,Al,Si) и зависимости 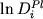 от 1/T.
Корреляция этих параметров во всех случаях
оказалась недостаточной, чтобы рекомендовать их
в качестве геотермометров природных
магматических равновесий. от 1/T.
Корреляция этих параметров во всех случаях
оказалась недостаточной, чтобы рекомендовать их
в качестве геотермометров природных
магматических равновесий.
Для решения задачи построения
надежного плагиоклазового геотермометра Дрейк предложил отказаться от
рассмотрения коэффициентов распределения и
перейти к анализу температурных зависимостей
для констант равновесия реакций
кристаллизации плагиоклазовых компонентов,
см. уравнения (1.30аб):
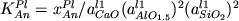 , (2.31а) , (2.31а)
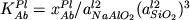 . (2.31б) . (2.31б)
Активности компонентов в плагиоклазе
были приравнены мольным долям анортита и альбита, что
подразумевает модель идеального
смешения компонентов в плагиоклазе. При таком
подходе главный вклад в интегральный эффект
неидеального смешения относится на счет
взаимодействия между компонентами расплава.
Выбор этих компонентов для
формального термодинамического описания
произволен: задача состояла в том, чтобы
попытаться найти такой набор компонентов жидкой
фазы, для которых замена активностей на
концентрации в уравнениях (2.31аб)
позволит эффективным образом учесть реакции
взаимодействия в расплаве и получить
максимально линейные зависимости 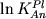 и и 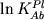 от 1/T. Для решения задачи построения
этой "субидеальной" модели Дрейк исследовал
два варианта активности компонентов расплава: l1
- модель идеального смешения однокатионных
оксидов и l2 - модифицированный вариант
модели (Bottinga, Weill,
1972). от 1/T. Для решения задачи построения
этой "субидеальной" модели Дрейк исследовал
два варианта активности компонентов расплава: l1
- модель идеального смешения однокатионных
оксидов и l2 - модифицированный вариант
модели (Bottinga, Weill,
1972).
В первом случае в качестве компонентов
расплава выступают молекулы вида SiO2, AlO1.5,
FeO, NaO0.5 и т.д.; согласно второй модели
силикатную жидкость можно рассматривать как
идеальную смесь неассоциированных (MgO, FeO, SiO2)
и ассоциированных молекул11 . Различие
подходов Дрейка и Боттинга-Вейла состояло в том,
что разделив компоненты расплава на две группы -
"модификаторы" (TiO2,
MgO, FeO, CaOизб) и "сеткообразователи"
(SiO2, KAlO2, NaAlO2, CaAl2O4),
первый автор постулировал идеальное смешение
компонентов только одного типа. Формально это
означало, что активность, скажем кремнезема,
рассчитывается как отношение количества молей SiO2
к сумме молекулярных количеств
"сеткообразователей", что подразумевает
отсутствие взаимодействия (смешения) с
"модификаторами" - такие модели получили
название двухрешеточных
(two lattice models).
В результате анализа температурных
зависимостей констант равновесия, рассчитанных
для каждого компонента по двум рассмотренным
выше моделям, было установлено, что наилучшая
линейная корреляция наблюдается для зависимости
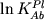 от 1/T, где значения константы
равновесия от 1/T, где значения константы
равновесия 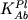 рассчитывались с
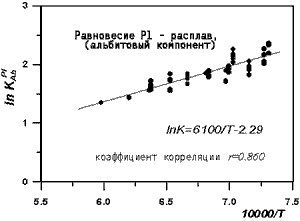
использованием двухрешеточной модели l2 (Рис. 2.17). Эту зависимость было
предложено использовать в качестве
плагиоклазового термометра, который по
результатам независимого тестирования
гарантировал точность порядка 20оС (Арискин, Бармина,
1990). рассчитывались с
использованием двухрешеточной модели l2 (Рис. 2.17). Эту зависимость было
предложено использовать в качестве
плагиоклазового термометра, который по
результатам независимого тестирования
гарантировал точность порядка 20оС (Арискин, Бармина,
1990).
|
Рис. 2.17.
Зависимость константы равновесия
реакции кристаллизации альбитового
компонента плагиоклаза от температуры
Данные (Drake, 1976): для расчета 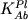
использована двухрешеточная модель
сеткообразователей
и модификаторов |
Полученный результат
свидетельствовал, что предложенная Дрейком двухрешеточная модель может
действительно отражать свойства смешения
компонентов в силикатной жидкости, в частности
отсутствие "свободных" катионов щелочных
металлов и их ассоциированность с алюмокислородными
тетраэдрами. Парадокс состоял в том, что
кристаллизация анортита, наоборот,
лучше описывалась при использовании модели
однокатионных оксидов l1 (см. параметры в
Табл. 1.1). Было высказано
предположение, что это связано с особенностями
свойств смешения CaO в силикатных расплавах (Drake, 1976). Это
допущение получило подтверждение в последующих
работах Нильсена с коллегами (Nielsen, Drake, 1979;
Nielsen, Dungan, 1983).
Нильсен и Дрейк предприняли
термодинамический анализ результатов
экспериментов, описывающих равновесие Px-расплав
(Nielsen, Drake, 1979).
Несмотря на то, что в период подготовки этой
работы в литературе практически отсутствовали
надежные данные о распределении петрогенных
элементов между пироксенами и
силикатной жидкостью, этим авторам удалось
сформировать выборку составов, представляющих
несколько десятков предположительно
"равновесных" экспериментов. Эти опыты были
проведены при температурах 1108-1320°С в диапазоне fО2
примерно от 10-8 до 10-14 атм. Составы
исходных смесей варьировали в широких пределах -
от низкожелезистых с сильно колеблющимися
содержаниями щелочей и Al2O3 до
высокожелезистых и низкощелочных лунных
базальтов. Имеющиеся данные Нильсен и Дрейк
разделили на две группы: одна включала 32 пары
составов сосуществующих высоко-Са пироксенов (Aug)
и расплавов, вторая - 31 пару составов низко-Са
пироксенов (Opx и Pig) и расплавов.
Термодинамическая обработка данных проводилась
раздельно для каждой из выделенных групп, без
разделения железа в расплаве на закисную и
окисную формы. Авторы акцентировали внимание на
реакциях кристаллизации вида
MeO(NM) + SiO2(NF)=MeSiO3 (Px)
, (2.32)
где Me - Mg, Fe2+, Са (NM -
модификаторы, NF - сеткообразователи), а также
обменных равновесиях, таких как
MgO(NM) + FeSiO3(Px)=MgSiO3 (Px)
+ FeO(NM) . (2.33)
Всего было проанализировано более 30
способов расчета констант равновесия Px-расплав:
в 18 случаях использовалась двухрешеточная
модель силикатной жидкости, в остальных - модель однокатионных оксидов. Для
твердой фазы предполагалось идеальное смешение фиктивных
компонентов твердого раствора - MgSiO3, FeSiO3
и CaSiO3 (рассмотрено 24 уравнения) и
двухпозиционные модели, включающие расчет
активностей энстатита, ферросилита,
геденбергита и диопсида
с учетом распределения катионов по позициям M1
и M2 - 8 уравнений. Результаты этого анализа
позволили сформулировать два вывода: 1. наилучшие
результаты получены при использовании двухрешеточной
модели смешения в жидкой фазе, 2. различия в
моделях смешения компонентов твердых растворов
с точки зрения точности предлагаемых геотермометров
оказались незначимы (Nielsen, Drake, 1979).
Другой важный результат этого
исследования состоит в том, что в предложенную
ранее двухрешеточную модель
силикатной жидкости (Drake, 1976) было
внесено небольшое, но принципиальное изменение -
оксид кальция был полностью отнесен к числу
компонентов-модификаторов, а "сеточный"
компонент CaAl2O4 из рассмотрения
исключался. При этом избыток алюминия
относительно щелочей также переводился в группу
модификаторов. Максимально точные геотермометры
Aug - расплав (1 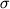 =18.8oC) и низко-Са Px -
расплав (1 =18.8oC) и низко-Са Px -
расплав (1 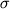 =22.4oC) были получены при
использовании этого нового модифицированного
варианта модели Боттинга-Вейла. Некоторые из
этих пироксеновых геотермометров
использовались нами на начальном этапе
построения моделей фракционирования
базальтовых магм (Арискин,
Френкель, 1982) - Табл.
1.1. Завершая этот экскурс, отметим, что
двухрешеточная модель строения расплава
наиболее последовательно была задействована в
работе (Nielsen, Dungan,
1983)12 . =22.4oC) были получены при
использовании этого нового модифицированного
варианта модели Боттинга-Вейла. Некоторые из
этих пироксеновых геотермометров
использовались нами на начальном этапе
построения моделей фракционирования
базальтовых магм (Арискин,
Френкель, 1982) - Табл.
1.1. Завершая этот экскурс, отметим, что
двухрешеточная модель строения расплава
наиболее последовательно была задействована в
работе (Nielsen, Dungan,
1983)12 .
Таким образом, представления об
ассоциированности молекул расплава, которые
вытекали из данных по физическим свойствам (Bottinga, Weill, 1972)
трансформировались в эмпирическую модель
двухрешеточного строения силикатной жидкости,
основанную на данных по фазовым равновесиям
минерал-расплав (Drake,
1976; Nielsen, Drake, 1979; Nielsen, Dungan, 1983).
На этой модели основаны большинство уравнений
равновесия, составляющих термодинамический
базис моделей КОМАГМАТ, ЛУНАМАГ
и МЕТЕОМОД.
Расчет активностей компонентов в
силикатной жидкости по модели (Nielsen, Drake, 1979;
Nielsen, Dungan, 1983) проводится в следующей
последовательности:
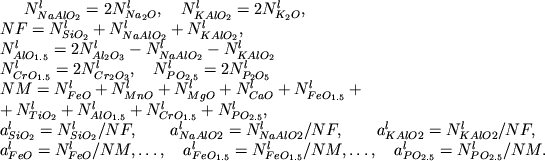 (2.34) (2.34)
Этот алгоритм предполагает, что сумма
щелочей Na2O+K2O не превышает общее
содержание Al2O3 в расплаве и уравнения
(2.34) применимы для систем низкой и умеренной
щелочности.
Несмотря на то, что представленная
здесь двухрешеточная модель
силикатной жидкости доказала практически
свою эффективность при описании равновесий Pl-расплав
и Px-расплав, она неоднократно подвергалась
критике за некоторую термодинамическую
противоречивость. В частности, И.Д.Рябчиков
отмечал, что использование уравнений Нильсена и
Дрейка "приводит к абсурдным результатам, если
их применять к составам с широкими вариациями
отношения элементов сеткооборазователей
к модификаторам" (Магматические горные
породы..., 1987, стр. 356). Не менее жесткая критика
прозвучала в работе (Гиорсоу,
1992), который обратил внимание, что "константы
равновесия, полученные Нильсеном и Дунганом, не
согласуются с имеющимися данными по
термодинамическим свойствам твердых фаз и
расплава в стандартном состоянии". Тем не менее,
трудно оспорить тот факт, что использование этой
казалось бы "абсурдной" двухрешеточной модели
позволяет резко повысить точность геотермометров
минерал-расплав и удачно согласовывать данные
сотен экспериментов, полученных в десятках
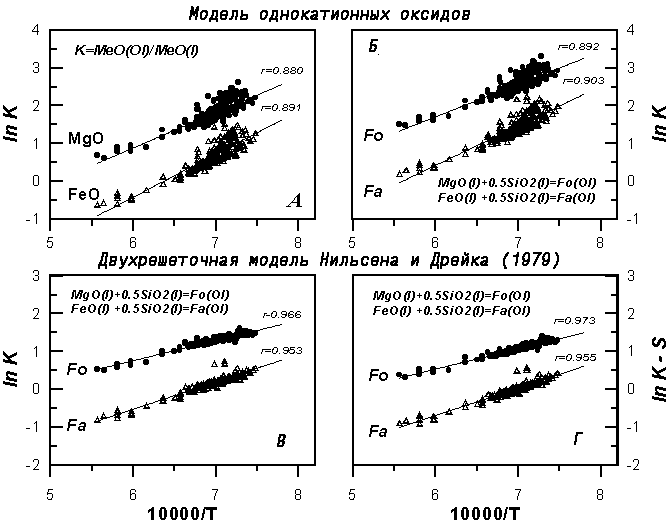
различных лабораторий. Для иллюстрации этого мы
приводим данные по равновесию Ol-расплав,
обработанные без учета и с учетом двухрешеточной
модели строения силикатного расплава (Рис. 2.18).
|
Рис. 2.18.
Зависимость коэффициентов распределения и
констант равновесия
для реакций кристаллизации оливиновых
компонентов от температуры
А Молекулярные коэффициенты
распределения; константы равновесия:
Б активности компонентов расплава
рассчитаны по модели однокатионных оксидов;
В и Г - использована двухрешеточная
модель строения расплава.
Вариант Г включает дополнительную поправку
на неидеальность расплава путем
введения фактора состава ![$S = \beta \ln [Si/(Si + Al)]^l$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula41.gif) , , 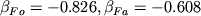 (см. ниже) (см. ниже) |
Здесь показаны результаты
термодинамической обработки данных 213
экспериментов, характеризующих равновесие Ol-расплав
для сухих толеитовых систем (48 < SiO2 < 65%)
при атмосферном давлении. Эти данные были
найдены при помощи поисковой системы ИНФОРЕКС-4.0
и представляют 20 независимых экспериментальных
исследований. Продолжительность опытов во всех
случаях составляла не менее 48 часов, что
позволяет предполагать равновесное
распределение ионов Mg2+ и Fe2+ между
оливином и расплавом. Параметры показанных на Рис. 2.18 регрессионных линий были
использованы для решения обратной задачи -
расчета температур равновесия по составам
сосуществующих фаз. Эти данные показали, что при
переходе к двухрешеточной модели
жидкости точность геотермометров
возрастает в 2.5-3 раза и достигает примерно  10оС. 10оС.
Термодинамическая интерпретация этого
факта предполагает объяснение причин, по
которым активность кремнезема (см. систему 2.34) может не сильно
отличаться от 0.90-0.95 в широком диапазоне
содержаний SiO2 - ведь для толеитовых систем
характерны низкие содержания щелочей. Это
подразумевает и ответ на вопрос, почему при
использовании двухрешеточной модели активность
в расплаве Fo, Fa, En и других фемических
компонентов, практически не зависит от
активности кремнезема и определяется
концентрацией соответствующего катиона среди компонентов-модификаторов? Для его
решения необходимо привлечь представления о
структурном состоянии силикатной жидкости и тех
реальных частицах, которые должны определять
активности компонентов в реакциях
кристаллизации.
Из анализа литературы можно сделать
вывод, что большинство исследователей
рассматривают силикатные расплавы как
ионно-полимерные системы, где "ионная часть"
представлена преимущественно двухвалентными
катионами (Mg2+, Mn2+, Fe2+, Ca2+),
которые обеспечивают баланс заряда в различной
степени полимеризованных кремнекислородных
группировок, см. обзоры (Hess, 1995; Mysen, 1995).
Присутствие тетраэдрически координированных
ионов алюминия Al3+ способствует
дополнительной полимеризации силикатной
жидкости, причем условие локальной
электронейтральности для полимеризованных
частиц 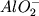 осуществляется в основном за счет
катионов щелочных металлов. Данные
рамановской спектроскопии указывают на то, что
часть ионов Al3+ определенно присутствует и
в октадрическом окружении кислородом, что
подразумевает одновременное существование
свободных радикалов осуществляется в основном за счет
катионов щелочных металлов. Данные
рамановской спектроскопии указывают на то, что
часть ионов Al3+ определенно присутствует и
в октадрическом окружении кислородом, что
подразумевает одновременное существование
свободных радикалов 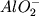 (Mysen, 1995). (Mysen, 1995).
Принципы термодинамического описания
ионизированных систем были сформулированы Д.С.Коржинским, однако предсказательные
возможности гипотезы
кислотно-основного взаимодействия (Коржинский, 1959)
не позволяют говорить о полной совместимости
этой концепции с данными о строении
полимеризованных силикатных расплавов (Hess, 1995; Mysen, 1995).
В дальнейшем, попытки связать данные по фазовым
равновесиям и термодинамические модели
силикатных систем предпринимались неоднократно
(работы Куширо, Боттинги,
Перчука, Хесса, Майсена, Анфилогова
и многих других). В контексте проблемы
двухрешеточной модели расплава целесообразно
обратиться к методу Брэдли (Bradley, 1962ab, 1964).
Этот автор предложил для описания
реакций с участием свободных катионов и
полимеризованных анионных группировок
использовать уравнения, учитывающие степень
полимеризации (Bradley,
1964). При таком подходе обычная реакция
кристаллизации, скажем энстатитового компонента
пироксенов
Mg2+(l) + 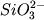 (l)=MgSiO3 (Px)
, (2.35) (l)=MgSiO3 (Px)
, (2.35)
записывается в виде
Mg2+(l) + 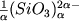 (l)=MgSiO3 (Px), (2.36) (l)=MgSiO3 (Px), (2.36)
где 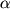 отвечает
среднестатистическому числу "частиц" отвечает
среднестатистическому числу "частиц" 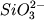 в
полимеризованной цепочке. Константа равновесия
реакции (2.36) включает активность метасиликатного
аниона в полимеризованной форме в
полимеризованной цепочке. Константа равновесия
реакции (2.36) включает активность метасиликатного
аниона в полимеризованной форме
![$K_{En}^{Px - l} = a_{En}^{Px} /a_{Mg^{2 + } }^l [a_{(SiO_3 )_\alpha ^{2\alpha - } }^l ]^{1/\alpha }$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula50.gif) , (2.37) , (2.37)
что принципиально отличает уравнение
(2.37) от выражений типа (1.21)
или (2.31), где используется
некоторая интегральная и одинаковая для всех
реакций активность SiO2 в жидкости.
Анализ соотношения (2.37)
приводит к выводу, что при увеличении степени
полимеризации 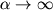 величина величина 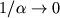 ,
поэтому значение члена, отвечающего за
активность кременезема, стремится к 1.
Возрастание степени полимеризации
сопровождается резким уменьшением общего числа
заряженных частиц, так что величина ,
поэтому значение члена, отвечающего за
активность кременезема, стремится к 1.
Возрастание степени полимеризации
сопровождается резким уменьшением общего числа
заряженных частиц, так что величина 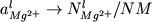 , где NM - общее количество
катионов. Таким образом, ионно-полимерная
трактовка расплавно-минеральных равновесий
приводит к тем же соотношениям
активность-состав, которые следуют из анализа
чисто эвристической двухрешеточной модели
строения силикатной жидкости. , где NM - общее количество
катионов. Таким образом, ионно-полимерная
трактовка расплавно-минеральных равновесий
приводит к тем же соотношениям
активность-состав, которые следуют из анализа
чисто эвристической двухрешеточной модели
строения силикатной жидкости.
По мнению авторов это совпадение не
случайно, а методика Брэдли
заслуживает более пристального внимания
специалистов в области термодинамики
расплавно-минеральных равновесий. Этот подход
может быть согласован с экспериментальными
данными по распределению в расплаве кремне- и
алюмокислородных группировок (Hess, 1995; Mysen, 1995)
и позволяет критически взглянуть на некоторые
петрологические модели, включающие, например,
понятие интегральной активности кремнезема или
сродства минералов к SiO2 в силикатной
жидкости (Гиорсоу,
Кармайкл, 1992).
Геотермометры для силикатных фаз
Данные рамановской
спектроскопии показывают, что главными
"кирпичиками" силикатных расплавов являются
кремнекислородные радикалы 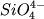 , , 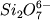 , , 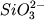 , , 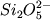 и SiO2 (Hess, 1995; Mysen, 1995).
Это означает, что при записи реакций
кристаллизации компонентов оливинов, пироксенов
и плагиоклазов в уравнениях вида (2.36) должны участвовать разные
формы кремнезема. Общим является то, что условие
полимеризации обуславливает слабую зависимость
соответствующих констант равновесия от валового
содержания в расплаве SiO2 (2.37). В этом смысле становится
понятным, почему двухрешеточная модель
расплава хорошо описывает расплавно-минеральные
равновесия в широком диапазоне - от базальтов
до дацитов (Рис. 2.18ВГ). и SiO2 (Hess, 1995; Mysen, 1995).
Это означает, что при записи реакций
кристаллизации компонентов оливинов, пироксенов
и плагиоклазов в уравнениях вида (2.36) должны участвовать разные
формы кремнезема. Общим является то, что условие
полимеризации обуславливает слабую зависимость
соответствующих констант равновесия от валового
содержания в расплаве SiO2 (2.37). В этом смысле становится
понятным, почему двухрешеточная модель
расплава хорошо описывает расплавно-минеральные
равновесия в широком диапазоне - от базальтов
до дацитов (Рис. 2.18ВГ).
Известно, однако, что степень
полимеризации силикатной жидкости сильно
зависит от общего отношения Si/O и температуры,
понижаясь при смещении в область более
высокотемпературных и обогащенных оливином
составов, например (Hess,
1980). Это накладывает определенные ограничения
на использование геотермометров,
построенных по методике Нильсена. В
нашей работе мы обычно проводили калибровки в
диапазоне кремнекислотности 45 < SiO2 < 65% и
температур 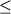 1300оС. Серия геотермометров
минерал-расплав, использованных в базовой версии
модели КОМАГМАТ приведена в Табл.
2.4. 1300оС. Серия геотермометров
минерал-расплав, использованных в базовой версии
модели КОМАГМАТ приведена в Табл.
2.4.
Таблица 2.4. Параметры
геотермометров минерал-расплав для модели КОМАГМАТ
Минерал |
Компо-нент |
Параметры
геотермометров |
Число точек |
Ссылка |
Оливин
(Ol) |
Fo (1) |
\ln K = 5543/T - 2.32 + 0.210ln (Al/Si) |
67 |
Ariskin et al.,1993 |
Fa (2) |
ln K = 6457/T - 4.22 + 0.084ln (Al/Si) |
Плагиоклаз
(Pl) |
An (3) |
ln K = 10641/T - 1.32 + 0.369ln R |
58 |
Арискин,Бармина, 1990 |
Ab (4) |
ln K = 11683/T - 6.16 - 0.119ln R |
Авгит
(Aug) |
En (5) |
ln K = 8521/T - 5.16 |
25 |
Арискин и др.,1986 |
Fs (6) |
ln K = 13535/T - 9.87 |
Wo (7) |
ln K = 2408/T - 1.24 |
Al01.5 |
D=0.20 |
Пижонит
(Pig) |
En (8) |
ln K = 8502/T - 4.74 |
18 |
Арискин и др.,1986 |
Fs (9) |
ln K = 5865/T - 4.04 |
Wo (10) |
ln K = 4371/T - 4.02 |
Al01.5 |
D = 0.10 |
Ортопироксен
(Opx) |
En (11) |
ln K = 7208/T - 3.71 |
39 |
Болиховскаяи др., 1995 |
Fs (12) |
ln K = 6386/T - 4.39 |
Wo (13) |
ln K = 11950/T - 10.40 |
Al01.5 |
D = 0.10 |
Примечания. R = ln [(Na + K)Al/Si2 ].
Оливин. В 1986-1990 гг. мы провели
полную перекалибровку термодинамической основы
моделей РТРК и ТОЛЕМАГ
(Арискин и др., 1986),
обработав результаты экспериментов по плавлению
земных пород основного и среднего состава,
используя подход (Nielsen,
Dungan, 1983). Эти опыты были проведены в период
1974-1988 гг., а исходные для них материалы
представлены субщелочными базальтами,
абиссальными толеитами, известково-щелочными
лавами и пироксен-порфировыми базальтами срединных хребтов. Для
термодинамической обработки данных по
равновесию Ol-расплав были выбраны составы
стекол, содержащие от 45 до 60 мас.% SiO2 при
общей щелочности Na2O+K2O 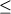 4 мас.%.
Данные эксперименты охватывают диапазон
температур 1070-1300оС и летучести кислорода -14 4 мас.%.
Данные эксперименты охватывают диапазон
температур 1070-1300оС и летучести кислорода -14
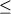 logfO2 logfO2 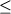 -8; продолжительность опытов
составляла не менее 48 часов. -8; продолжительность опытов
составляла не менее 48 часов.
На первом этапе обработки при помощи
уравнения (Sack et al.,
1980) проводилось разделение железа в расплаве
на Fe3+ и Fe2+, затем рассчитывались
коэффициенты сокристаллизации 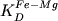 . Из
дальнейшего рассмотрения исключались пары
составов, для которых не выполнялось условие 0.30 . Из
дальнейшего рассмотрения исключались пары
составов, для которых не выполнялось условие 0.30 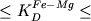 0.36 - в конечном итоге было отобрано 67
пар составов оливин-расплав. В результате
обработки этих данных по линейной модели (1.19б)
было получено 2 геотермометра, характеризующихся
высокими коэффициентами корреляции ln K от 1/T: 0.36 - в конечном итоге было отобрано 67
пар составов оливин-расплав. В результате
обработки этих данных по линейной модели (1.19б)
было получено 2 геотермометра, характеризующихся
высокими коэффициентами корреляции ln K от 1/T:
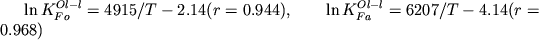 . (2.38) . (2.38)
Несмотря на наличие сильной
корреляционной связи, было установлено, что при
таком способе обработки значения 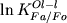 для более глиноземистых составов оказываются
обычно выше регрессионных линий, а для менее
глиноземистых - ниже (Арискин
и др., 1986).
для более глиноземистых составов оказываются
обычно выше регрессионных линий, а для менее
глиноземистых - ниже (Арискин
и др., 1986).
Чтобы уменьшить влияние состава на
расчетные температурные зависимости, логарифм
отношения Al/Si в расплаве был включен в качестве
дополнительного параметра в уравнение для
калибровки
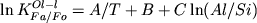 . (2.39) . (2.39)
Значения соответствующих
регрессионных коэффициентов для Fo- и Fa-геотермометров
приведены в Табл. 2.4 (уравнения
1 и 2).
При использовании этих уравнений
совместно интегральный Ol-термометр в 70%
случаев воспроизводит экспериментальные
температуры для 67 исходных стекол с точностью
порядка  10оС (Рис. 2.19А). При этом
отклонения рассчитанных составов оливина от
экспериментальных не превышают 2 мол.% Fo и
составляют в среднем 0.5-0.7 мол.% Fo. 10оС (Рис. 2.19А). При этом
отклонения рассчитанных составов оливина от
экспериментальных не превышают 2 мол.% Fo и
составляют в среднем 0.5-0.7 мол.% Fo.
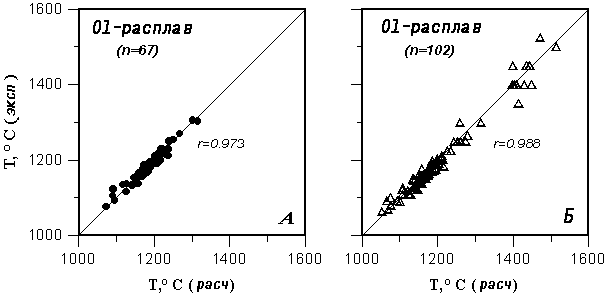
|
Рис. 2.19.
Сравнение экспериментальных и расчетных
температур равновесия
оливин - расплав для умеренно щелочных систем при
атмосферном давлении
Расчеты температур насыщения
расплавов оливином проведены с использованием
Fo и Fa геотермометров из Табл. 2.4.
Экспериментальная информация получена при
помощи базы данных ИНФОРЭКС-4.0: А Результаты
исследований, которые
использовались при калибровке уравнений
равновесия
Ol-расплав (работы 1974-1988 гг.); Б независимые
данные, полученные в период 1989-1996 гг. |
При подготовке монографии мы провели
дополнительное тестирование базовых оливиновых
геотермометров модели КОМАГМАТ
на независимой выборке экспериментальных
данных, которые были опубликованы после 1988 г. Эта
выборка была сформирована при помощи программы ИНФОРЭКС-4.0 и отвечает тем же
поисковым критериям, которые были использованы
ранее при калибровке. Результаты сравнения
экспериментальных и расчетных температур
приведены на Рис. 2.19Б. Эти данные показывают,
что в диапазоне 1050оС < T < 1300оС
модель реалистично предсказывает температуры
равновесия Ol-расплав. При температурах выше
1400оС отдельные отклонения могут достигать
40-50оС. Как показывает опыт, эти погрешности
могут быть минимизированы при использовании в
калибровках других композиционных параметров
или их сочетаний (см. Рис. 2.18Г).
Плагиоклаз. В дальнейшем, метод
композиционных поправок использовался нами
при разработке максимально точных геотермометров
минерал-расплав для широкого диапазона
составов. Термодинамический смысл добавочных
членов в уравнениях равновесия очевиден: эти
поправки представляют эффективный способ учета
неидеальности смешения компонентов в рамках двухрешеточной модели расплава. С
определенной долей условности их можно
трактовать как произведение неизвестных
коэффициентов активности компонентов, которое
описано эмпирически в виде зависимости от
состава жидкой фазы. Этот подход к калибровке
уравнений равновесия оказался эффективным при
разработке новых геотермометров Pl-расплав.
При использовании плагиоклазовых
термометров Дрейка (Табл.
1.1) в расчетах кристаллизации толеитовых
магм выяснилось, что они дают надежные оценки
температур в узком диапазоне составов - примерно
от 49 до 55 мас.% SiO2 (Арискин и др., 1986,1987).
В случае, когда содержание SiO2 < 49 мас.%,
расчетные температуры кристаллизации Pl на
20-30°С ниже экспериментальных; для интервала 55
<SiO2 < 65% эти отклонения положительны и
составляют 20-50°С. При этом было установлено, что в
области высокотемпературных Ol-Pl котектик
(при 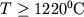 ) наблюдается тенденция к
занижению на 5-7 мол.% модельного содержания An
в Pl. Это потребовало пересмотра исходных
данных для калибровок плагиоклазовых
геотермометров и более тщательного исследования
вопроса о выборе оптимальной модели силикатной
жидкости. С этой целью были систематизированы
данные по равновесию Pl - расплав, полученные в
экспериментах на природных составах (Grove, Bryan, 1983; Mahood,
Baker, 1986; Sack et al., 1987; Tormey et al., 1987). Эта
информация включает данные 158 закалочных опытов,
проведенных при температурах 1026-1235оС на
образцах базальтов и андезитов, представляющих толеитовые, известково-щелочные
и щелочно-базальтовые серии. При
термодинамическом анализе этих данных мы
ограничились рассмотрением выборки из 58
"наиболее равновесных" опытов,
продолжительность которых составляла не менее 4
суток (96 часов), а составы расплавов не выходили
за пределы систем умеренной щелочности Na2O+K2O ) наблюдается тенденция к
занижению на 5-7 мол.% модельного содержания An
в Pl. Это потребовало пересмотра исходных
данных для калибровок плагиоклазовых
геотермометров и более тщательного исследования
вопроса о выборе оптимальной модели силикатной
жидкости. С этой целью были систематизированы
данные по равновесию Pl - расплав, полученные в
экспериментах на природных составах (Grove, Bryan, 1983; Mahood,
Baker, 1986; Sack et al., 1987; Tormey et al., 1987). Эта
информация включает данные 158 закалочных опытов,
проведенных при температурах 1026-1235оС на
образцах базальтов и андезитов, представляющих толеитовые, известково-щелочные
и щелочно-базальтовые серии. При
термодинамическом анализе этих данных мы
ограничились рассмотрением выборки из 58
"наиболее равновесных" опытов,
продолжительность которых составляла не менее 4
суток (96 часов), а составы расплавов не выходили
за пределы систем умеренной щелочности Na2O+K2O
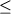 4 мас.% (Арискин,
Бармина, 1990). В результате обработки этих
данных по методике Нильсена и Дунгана
(1983) было получено два уравнения: 4 мас.% (Арискин,
Бармина, 1990). В результате обработки этих
данных по методике Нильсена и Дунгана
(1983) было получено два уравнения:
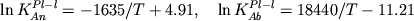 . (2.40) . (2.40)
Соотношения для альбитового
компонента представляют хороший геотермометр,
обеспечивающий точность порядка 10оС,
однако для анортита параметры регрессии
указывают на практическое отсутствие
зависимости 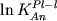 от 1/T - это
потребовало повторного пересмотра и модификации
двухрешеточной модели расплава. Мы исследовали
несколько новых вариантов распределения
алюминия между модификаторами и сеткообразователями, обнаружив, что
при включении AlO1.5 в число
каркасообразующих компонентов от 1/T - это
потребовало повторного пересмотра и модификации
двухрешеточной модели расплава. Мы исследовали
несколько новых вариантов распределения
алюминия между модификаторами и сеткообразователями, обнаружив, что
при включении AlO1.5 в число
каркасообразующих компонентов 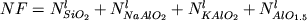 (2.34) зависимость (2.34) зависимость 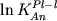 от 1/T приобретает положительный наклон,
сравнимый с температурной зависимостью для
альбита (Арискин,
Бармина, 1990). Максимальной точности этих
геотермометров удалось добиться при включении в
уравнения регрессии дополнительного фактора
состава от 1/T приобретает положительный наклон,
сравнимый с температурной зависимостью для
альбита (Арискин,
Бармина, 1990). Максимальной точности этих
геотермометров удалось добиться при включении в
уравнения регрессии дополнительного фактора
состава ![$\ln [(Na + K)Al/Si^2 ]$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula74.gif) , см. Табл. 2.4. Таким образом,
для базовой выборки данных 58 экспериментов
совместное использование уравнений для An и Ab
(Табл. 2.4) позволяет
воспроизвести экспериментальные температуры в
70% случаев с точностью не ниже 10оС (Рис. 2.20А). При этом среднее
отклонение экспериментальных и рассчитанных
составов Pl составляет 2.8 мол.% An. , см. Табл. 2.4. Таким образом,
для базовой выборки данных 58 экспериментов
совместное использование уравнений для An и Ab
(Табл. 2.4) позволяет
воспроизвести экспериментальные температуры в
70% случаев с точностью не ниже 10оС (Рис. 2.20А). При этом среднее
отклонение экспериментальных и рассчитанных
составов Pl составляет 2.8 мол.% An.
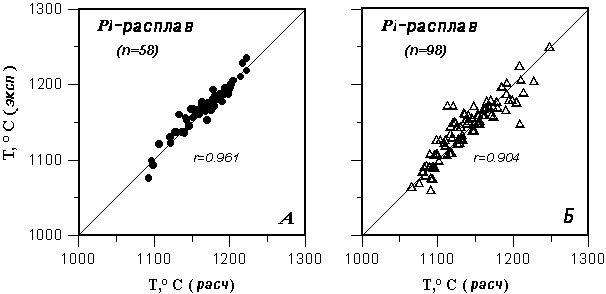
|
Рис. 2.20.
Сравнение экспериментальных и расчетных
температур равновесия
плагиоклаз-расплав для умеренно щелочных систем
при атмосферном давлении
Расчеты температур насыщения
расплавов плагиоклазом проведены с
использованием
An и Ab геотермометров из Табл. 2.4.
Экспериментальная информация получена при
помощи базы данных ИНФОРЭКС-4.0: А Результаты
исследований, которые использовались
при калибровке уравнений равновесия Pl-расплав
(работы 1982-1987 гг.);
Б независимые данные, полученные в период 1988-1996
гг. |
На рис. 2.20Б показаны результаты
тестирования этих плагиоклазовых
геотермометров на независимых
экспериментальных данных, опубликованных после
1987 г. При выборке данных для сравнения при помощи
системы ИНФОРЭКС-4.0 мы ввели
менее жесткий критерий на продолжительность
опытов  часов и несколько расширили
диапазон щелочности закалочных стекол Na2O+K2O часов и несколько расширили
диапазон щелочности закалочных стекол Na2O+K2O
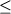 5 мас.%. Тем не менее интегральный Pl-геотермометр
показал хорошую воспроизводимость результатов 98
опытов, представляющих 14 различных
экспериментальных исследований. 5 мас.%. Тем не менее интегральный Pl-геотермометр
показал хорошую воспроизводимость результатов 98
опытов, представляющих 14 различных
экспериментальных исследований.
После 1990 г. уравнения равновесия Pl-расплав
для модели КОМАГМАТ не
перекалибровывались (Табл. 2.4).
Использование этих термометров показало, что
наилучшим образом они работают при температурах
1120-1200оС: при T<1120оС в области
андезит-базальтовых и андезитовых составов
отмечается занижение на 10-15оС расчетных
температур (при этом модельный состав
плагиоклаза может быть избыточно обогащен Ab);
при T > 1200оС в области
высокоглиноземистых магм расчетные температуры
систематически превышают экспериментальные. При
практических вычислениях это учитывается путем
введения небольших температурных поправок,
которые задаются на начальном этапе работы с
программой КОМАГМАТ при помощи
специально разработанного интерфейса (см. ниже).
Авгит. Включение
геотермометров высоко-Са Px - расплав (Nielsen, Drake, 1979
- Табл. 1.1) в алгоритм
моделирования траекторий равновесной
кристаллизации показало, что при их
использовании корректно предсказывается общий
порядок появления авгита на ликвидусе, однако
температуры кристаллизации этого пироксена
занижены на 15-20оС (Френкель, Арискин,
1984б). Появление новых экспериментальных
данных в 1979-1983 гг. создало основу для уточнения и
модификации пироксеновых геотермометров (Walker et al., 1979; Grove et
al., 1982; Grove, Bryan, 1983). В этих работах
приводятся химические анализы 33 авгитов и
сосуществующих закалочных стекол. Здесь следует
особо отметить работы Гроува с коллегами (Grove et al., 1982; Grove,
Bryan, 1983), у которых продолжительность
экспериментальных плавок в области
низкотемпературных многофазовых равновесий
составляла от 100 до 600 часов. Несомненно, что
полученные ими данные и в наши дни не потеряли
своего значения в качестве характеристик
равновесного распределения элементов между
авгитом и силикатной жидкостью.
Тем не менее, при термодинамической
обработке этой информации мы исключили из
рассмотрения 8 пар составов Aug-расплав,
которые по величине 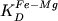 выходили за рамки
допустимых значений (Арискин
и др., 1986). Оставшиеся 25 пар анализов,
характеризующие распределение элементов в
диапазоне температур 1133-1193оС при среднем
значении выходили за рамки
допустимых значений (Арискин
и др., 1986). Оставшиеся 25 пар анализов,
характеризующие распределение элементов в
диапазоне температур 1133-1193оС при среднем
значении 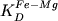 = 0.29 (1 = 0.29 (1 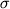 =0.03), были обработаны
по модели Нильсена и Дрейка - см. реакции (2.32). Рассчитанные
температурные зависимости для констант
равновесия реакций кристаллизации Еп, Fs и Wo приведены
в Табл. 2.4 (уравнения 5-7).
Разделение алюминия между авгитом и расплавом
было охарактеризовано при помощи среднего
коэффициента распределения =0.03), были обработаны
по модели Нильсена и Дрейка - см. реакции (2.32). Рассчитанные
температурные зависимости для констант
равновесия реакций кристаллизации Еп, Fs и Wo приведены
в Табл. 2.4 (уравнения 5-7).
Разделение алюминия между авгитом и расплавом
было охарактеризовано при помощи среднего
коэффициента распределения 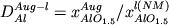 = 0.20 (1 = 0.20 (1 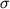 =0.09). =0.09).
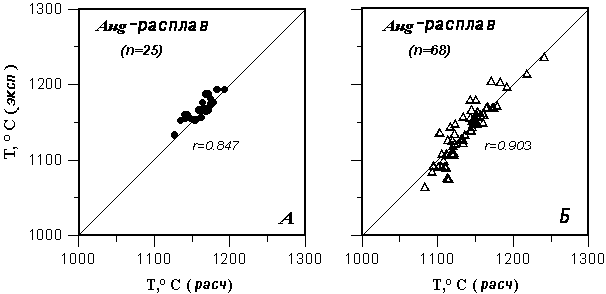
|
Рис. 2.21.
Сравнение экспериментальных и расчетных
температур равновесия
авгит-расплав для умеренно щелочных систем при
атмосферном давлении
Расчеты температур насыщения
расплавов авгитом проведены с
использованием пироксеновых геотермометров 5-7
из Табл. 2.4.
Экспериментальная информация получена при
помощи базы данных ИНФОРЭКС-4.0:
А Результаты исследований, которые
использовались при калибровке
уравнений равновесия Aug-расплав (работы 1979-1983 гг.);
Б независимые данные, полученные в период 1987-1996
гг. |
Приведенные в Табл. 2.4
параметры равновесия Aug-расплав были
включены в программу КОМАГМАТ и
использованы для расчета температур насыщения 25
исходных расплавов. В результате,
экспериментальные данные были воспроизведены в
72% случаев с точностью не ниже 10оС (Рис. 2.21А);
среднее отклонение расчетных температур от
экспериментальных составило 7.2оС.
Результаты тестирования этих пироксеновых
геотермометров на независимых
экспериментальных данных показаны на Рис. 2.21Б.
Пижонит и ортопироксен.
Выше отмечалось, что в основе уравнений,
предложенных ранее для описания равновесия
низко-Са Px - расплав, лежат результаты
обработки данных по составам пижонитов и
ортопироксенов (Nielsen,
Drake, 1979 - Табл. 1.1).
Эти уравнения были использованы для описания
кристаллизации из базальтового расплава
некоторой усредненной низкокальциевой
пироксеновой фазы (Арискин,
Френкель, 1982; Френкель, Арискин, 1984б).
Однако при моделировании кристаллизации
магматических расплавов мы убедились, что в
случае, когда одной из первых кристаллизующихся
фаз несомненно должен быть Opx, расчеты с
использованием геотермометров
Нильсена и Дрейка давали сильно заниженные
температуры появления на ликвидусе модельного
низко-Ca Рх. Это привело к необходимости
разделения экспериментальных данных на "пижонитовую"
и "гиперстеновую" серии и учета
при моделировании как минимум двух
разновидностей низкокальциевых пироксенов.
В работах (Grove
et al., 1982; Grove, Bryan, 1983) были приведены
составы 18 пар сосуществующих пижонитов и стекол,
характеризующих распределение элементов при
температурах 1059-1167оС. Рассчитанное по этим
данным среднее значение 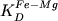 = 0.30 (1 = 0.30 (1 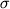 =0.04).
Обработка этой информации проводилась таким же
образом, как для авгитов - с использованием двухрешеточной модели (Nielsen, Drake, 1979; Nielsen,
Dungan, 1983). Параметры полученных
геотермометров Pig - расплав приведены в Табл. 2.4
(уравнения 8-10).
Разделение алюминия между пижонитом и расплавом
охарактеризовано при помощи среднего
коэффициента распределения =0.04).
Обработка этой информации проводилась таким же
образом, как для авгитов - с использованием двухрешеточной модели (Nielsen, Drake, 1979; Nielsen,
Dungan, 1983). Параметры полученных
геотермометров Pig - расплав приведены в Табл. 2.4
(уравнения 8-10).
Разделение алюминия между пижонитом и расплавом
охарактеризовано при помощи среднего
коэффициента распределения 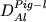 = 0.10 (1 = 0.10 (1 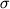 =0.05).
=0.05).
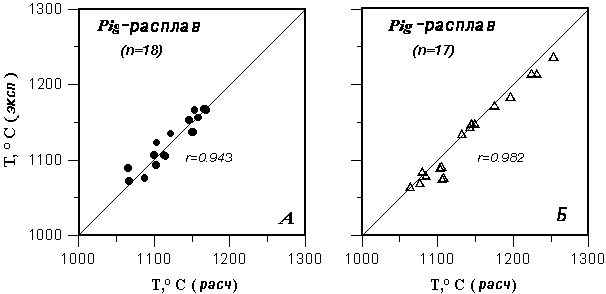
На Рис. 2.22А проведено сравнение
экспериментальных и рассчитанных при помощи
уравнений 8-10 (Табл. 2.4)
температур равновесия 18 исходных расплавов с
пижонитом. Эти результаты свидетельствуют, что в
69% случаев экспериментальные значения
температур воспроизводятся с точностью не ниже 10оС;
среднее отклонение расчетных температур от
экспериментальных составляет 7.9оС.
Тестирование этих пижонитовых геотермометров на
независимых экспериментальных также указывает
на хорошую точность предложенных уравнений (Рис.
2.22Б). Это особенно важно для моделирования
толеитовых систем, где пижонит является одной из
главных фаз на заключительных стадиях
кристаллизации магматических расплавов.
|
Рис. 2.22.
Сравнение экспериментальных и расчетных
температур равновесия
пижонит-расплав для умеренно щелочных систем при
атмосферном давлении
Расчеты температур насыщения
расплавов пижонитом проведены с
использованием пироксеновых геотермометров 8-10
из Табл. 2.4.
Экспериментальная информация получена при
помощи базы данных
ИНФОРЭКС-4.0: А Результаты исследований,
которые использовались
при калибровке уравнений равновесия Pig-расплав
(работы 1982-1983 гг.);
Б независимые данные, полученные в период
1987-1996 гг. |
Первые версии программы КОМАГМАТ
(в частности, ТОЛЕМАГ) включали геотермометры
Opx - расплав для En, Fs и Wo, построенные по
результатам обработки 13 экспериментов на
образцах лунных базальтов, земных андезитов и
некоторых синтетических составов (Луканин и др., 1986).
Совместное использование этих уравнений
равновесия гарантировало точность расчета
температур кристаллизации Opx порядка 10-15оС,
однако содержание СаO в модельных ортопироксенах
было завышено примерно в 2 раза. Перекалибровка Opx-термометров
была проведена на более представительном ряде
данных, включающем 39 экспериментов с образцами
земных базальтов и андезитов (Болиховская и др.,
1995). Эти опыты охватывают диапазон температур
1076-1339оС и летучести кислорода -12.2 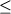 logfO2 logfO2
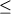 -6.1, а их продолжительность составляла не
менее 48 часов. Параметры полученных
ортопироксеновых геотермометров приведены в
Табл. 2.4 (уравнения 11-13).
Результаты тестирования этих зависимостей
указывают на точность 8-10оС; при этом
погрешности оценки состава Opx составляют 1-2
мол.%. Более полную информацию по калибровке Opx-термометров
можно найти в работе (Болиховская
и др., 1995). -6.1, а их продолжительность составляла не
менее 48 часов. Параметры полученных
ортопироксеновых геотермометров приведены в
Табл. 2.4 (уравнения 11-13).
Результаты тестирования этих зависимостей
указывают на точность 8-10оС; при этом
погрешности оценки состава Opx составляют 1-2
мол.%. Более полную информацию по калибровке Opx-термометров
можно найти в работе (Болиховская
и др., 1995).
Уравнения равновесия для железорудных
минералов
Несмотря на низкую
распространенность, шпинелиды и ильменит относятся к важным фазам
базальтовых систем, определяющим поведение в
кристаллизационном процессе FeO, Fe2O3 и
TiO2, а также некоторых примесных элементов,
таких как Cr и V. За последние 5-6 лет в литературе
накоплены данные сотен экспериментов по
плавлению силикатных систем с образованием этих
минералов, поэтому задача построения модели
фазовых равновесий, учитывающей кристаллизацию
оксидов железа и титана в настоящее время
представляется реальной. На раннем этапе
разработки моделей КОМАГМАТ
ситуация была менее оптимистичной: отдельные и
весьма фрагментарные данные для магнетита,
хромшпинелида и ильменита с трудом поддавались
согласованию и обработке. Это положение
осложнялось тем, что условия равновесия с
расплавом для Fe-Ti минералов зависят от летучести
кислорода, определяющей распределение
разновалентных форм железа и хрома. Тем не менее,
в 80-х годах было предпринято несколько попыток
описать условия насыщения магм магнетитом и
ильменитом с целью включения этих уравнений в
ЭВМ-модели кристаллизации базальтовых расплавов
(Nielsen, Dungan, 1983; Ghiorso,
1985; Ghiorso, Carmichael, 1985; Арискин и др., 1987).
В этой работе мы опирались на экспериментальные
данные (Hill, Roeder,
1974; Sack, 1982; Лапин
и др., 1985).
В результате обработки данных Сэка (1982) было получено
уравнение, характеризующее распределение Ti и Fe3+
в системе Mt-расплав:
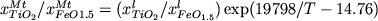 . (2.41) . (2.41)
Соотношение (2.41) можно
экстраполировать в область стехиометричных
титаномагнетитов ряда Fe3O4 -Fe2TiO4
( 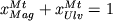 ) и использовать для оценки их
составов ) и использовать для оценки их
составов
![$x_{Mag}^{Mt} = 1/[2(x_{TiO_2 }^{Mt} /x_{FeO_{1.5} }^{Mt} ) + 1]$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula90.gif) , (2.42) , (2.42)
где Mag и Ulv - магнетитовый и ульвошпинеливый компоненты титаномагнетита.
На следующем этапе калибровки были использованы
дополнительные данные по температурам
кристаллизации Mt в толеитовых системах ферробазальтового состава (Hill, Roeder, 1974; Лапин и др., 1985).
Для этих экспериментов отсутствовали данные по
составам расплавов, равновесных с
титаномагнетитом, поэтому нам пришлось
воспользоваться результатами расчетов.
Используя программу ТОЛЕМАГ
(Арискин и др., 1986)
для двух исходных ферробазальтовых расплавов
были рассчитаны составы жидкостей, отвечающие
экспериментальным температурам появления
магнетита на ликвидусе (Hill, Roeder, 1974; Лапин и др., 1985).
Эти данные были обработаны по линейной модели
вида (1.19б) и
приведены к виду температурной зависимости
константы равновесия реакции кристаллизации
магнетитового компонента:
![$\ln [x_{Mag}^{Mt} /x_{FeO}^l (x_{FeO_{1.5} }^l )^2 ] = 34884/T - 14.97$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula91.gif) , (2.43) , (2.43)
где для расчета концентрации FeO и FeO1.5 в
расплаве использовалась модель
однокатионных оксидов. Система уравнений (2.41-2.43) описывает условия
насыщения базальтовых расплавов
титаномагнетитом и вплоть до 1997 г. была
задействована в модели КОМАГМАТ (Арискин и др., 1987).
При ее использовании удалось довольно точно
воспроизвести абсолютные температуры
кристаллизации железистой шпинели из расплавов
образцов 12017 (Лапин
и др., 1985) и GL-RHB (Hill, Roeder, 1974), а
также общий эффект расширения поля
кристаллизации Mt при переходе к более
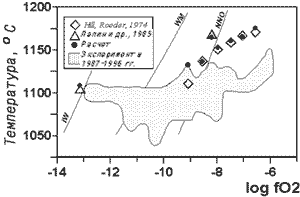
окислительным условиям - Рис. 2.23.
|
Рис. 2.23.
Сравнение экспериментальных и
расчетных температур кристаллизации
титаномагнетита
в ферробазальтовых системах при различных
окислительно-восстановительных условиях
Данные (Hill,
Roeder, 1974; Лапин и др.,
1985) были
использованы для построения уравнений
равновесия
Mt - расплав (2.41-2.43). Расчеты выполнены при
помощи программы КОМАГМАТ (Ariskin et al., 1993).
Сводка экспериментальных данных за
1987-1996 гг. по работе (Арискин,
1998). |
Тем не менее в последующем, именно
моделирование кристаллизации магнетита вызвало
определенные претензии со стороны специалистов
и пользователей программы КОМАГМАТ,
напр. (Yang et al., 1996).
Расчеты траекторий кристаллизации базальтовых
магм в условиях буферов QFM и NNO указывали
на систематическое завышение начальной
температуры кристаллизации Mt на 20-40оС.
Причина этих отклонений прояснилась после
сопоставления экспериментальных данных, на
которых проводилась калибровка, с результатами
других исследований (Рис. 2.23). Заштрихованное на
этом рисунке поле оконтуривает более 100
экспериментальных точек устойчивости
титаномагнетита, представленных в работах 1987-1996
гг. (Арискин, 1998).
Из этих данных можно сделать вывод о
наличии явного минимума температур
кристаллизации Ti-Mt между буферами WM
и NNO. В то время как калибровка
модели по 8 точкам (Hill,
Roeder, 1974; Лапин и
др., 1985) обеспечивала монотонное и
незначительное (порядка 8-10оС/logfO2)
изменение температуры Mt в зависимости от fO2.
Для учета этих отклонений в модели КОМАГМАТ
предусмотрена процедура коррекции рассчитанных
температур (Ariskin et
al., 1993), а недавно была проведена полная
перекалибровка "магнетитовой" модели: ее
результаты будут подробно рассмотрены в разделе,
посвященном ЭВМ-моделированию дифференциации
толеитовых магм (Глава 4).
Использованная в программе КОМАГМАТ
модель равновесия Ilm-расплав основана на
геотермометрах (Nielsen,
Dungan, 1983), которые были построены по
результатам 19 экспериментов с высоко-Ti лунными
базальтами при низкой фугитивности кислорода.
Состав модельных ильменитов ряда FeTiO3-Fe2O3
( 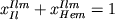 ) рассчитывался нами через
состав гипотетического сосуществующего Mt
при помощи эмпирического уравнения ) рассчитывался нами через
состав гипотетического сосуществующего Mt
при помощи эмпирического уравнения
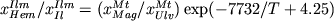 , (2.44) , (2.44)
полученного при обработке данных (Spencer, Lindsley, 1981).
Как и в случае с магнетитом, расчеты по
модели КОМАГМАТ приводили обычно
к занижению температур ильменита, в результате
чего он начинал кристаллизоваться при довольно
высоких содержаниях TiO2 в расплаве,
отвечающих примерно 6.5-7 мас.%. Эта
"ильменитовая" модель также была
перекалибрована и гарантирует теперь точность
расчета температур равновесия Ilm-расплав
порядка 10оС.
Учет общего давления
Простейший способ учета влияния
давления на фазовые равновесия состоит в задании
эмпирических коэффициентов, учитывающих
различный наклон ликвидусных поверхностей 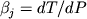 для разных минералов. Добавление приращения
температуры для разных минералов. Добавление приращения
температуры 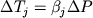 к значениям к значениям 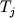 ,
рассчитанным при атмосферном давлении, не
требует изменения схемы алгоритма, показанной на
Рис. 2.1, и
позволяет учесть общий эффект смещения полей
кристаллизации минералов в зависимости от
давления. При построении выскобарной версии
модели КОМАГМАТ мы использовали модификацию
этого метода, учитывающую термодинамическую
природу зависимости фазовых равновесий от
давления (Арискин и
др., 1990, 1991). ,
рассчитанным при атмосферном давлении, не
требует изменения схемы алгоритма, показанной на
Рис. 2.1, и
позволяет учесть общий эффект смещения полей
кристаллизации минералов в зависимости от
давления. При построении выскобарной версии
модели КОМАГМАТ мы использовали модификацию
этого метода, учитывающую термодинамическую
природу зависимости фазовых равновесий от
давления (Арискин и
др., 1990, 1991).
Влияние давления на константу
равновесия реакции кристаллизации (1.25) при постоянной
температуре T выражается известным
соотношением:
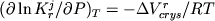 , (2.45) , (2.45)
где 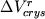 - объемный эффект
химической реакции. Отсюда приращение величины - объемный эффект
химической реакции. Отсюда приращение величины 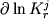 при изменении давления от при изменении давления от 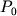 до до 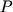
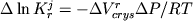 , (2.46) , (2.46)
где 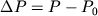 . В этом случае
интегральный эффект влияния температуры и
давления на константу равновесия можно
представить в виде . В этом случае
интегральный эффект влияния температуры и
давления на константу равновесия можно
представить в виде
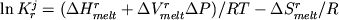 , (2.47) , (2.47)
где 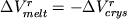 . По
аналогии с уравнением (2.47) эмпирические
геотермометры (1.19б),
характеризующие расплавно-минеральные
равновесия при давлении . По
аналогии с уравнением (2.47) эмпирические
геотермометры (1.19б),
характеризующие расплавно-минеральные
равновесия при давлении 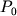 =1 атм, могут быть
преобразованы к виду =1 атм, могут быть
преобразованы к виду
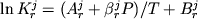 , (2.48) , (2.48)
где эмпирические коэффициенты 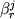 должны быть кратны объемному эффекту
плавления минала
должны быть кратны объемному эффекту
плавления минала 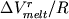 , а , а 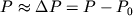 . Таким образом, задача сводится к определению
значений . Таким образом, задача сводится к определению
значений 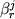 для каждого компонента данного
минерала. для каждого компонента данного
минерала.
Попытки использовать для этой цели
справочные данные по объемным эффектам
плавления Fo, Fa, En, Fs, Wo, An и Ab оказались не
слишком успешны (Арискин,
Горшков, 1984), поэтому было принято решение
опираться на прямые экспериментальные данные по
плавлению изверженных пород при высоких
давлениях. Для этой цели были выбраны результаты
экспериментов с образцами высокомагнезиальных
толеитов (> 10 мас.% MgO), проведенных в интервале
давлений 1 атм - 15 кбар (Bender et al., 1978; Green et
al., 1979; Fujii, Bougault, 1983). Эти данные включают
около 100 высокобарных опытов, которые
проводились при температурах 1200-1360оС в
сильно восстановительных условиях
графитовых капсул. Продолжительность опытов
варьировала при этом от 30 мин. до 4-5 часов и только
5 экспериментов имели длительность 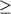 6 часов (Green et al., 1979). 6 часов (Green et al., 1979).
Главный результат этих работ
заключался в установлении сильной зависимости
температуры кристаллизации клинопироксена от
давления: при P < 10 кбар для всех составов
ликвидусной фазой являлся оливин, а в интервале
10-12 кбар первым кристаллизующимся минералом
становиnся клинопироксен авгитового состава (Рис. 2.24). Наклон линии Aug
ликвидуса составляет при этом около 15oC/кбар.
Положение ликвидусных линий для Ol и Pl
указывало, что эти минералы характеризуются
незначительной и примерно одинаковой
зависимостью температуры ликвидуса от давления -
порядка 5oC/кбар. Эти значения были
использованы в качестве ориентировочных
параметров при выборе оптимальных коэффициентов
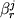 для различных миналов. для различных миналов.
Метод оценки параметров 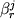 может
состоять в совместной обработке результатов 1
атм и высокобарических экспериментов по методу МНК
(2.48). Проблема состоит в
том, что качество данных, полученных при высоких
давлениях, сильно уступает результатам опытов
при 1 атм. На это указывает малая
продолжительность экспериментов (см. выше),
которая не гарантирует равновесное
распределение компонентов между минеральными
фазами и расплавом. Чтобы избежать влияния этого
фактора на все параметры равновесия (2.48), при поиске барических
коэффициентов мы фиксировали низкобарные
значения может
состоять в совместной обработке результатов 1
атм и высокобарических экспериментов по методу МНК
(2.48). Проблема состоит в
том, что качество данных, полученных при высоких
давлениях, сильно уступает результатам опытов
при 1 атм. На это указывает малая
продолжительность экспериментов (см. выше),
которая не гарантирует равновесное
распределение компонентов между минеральными
фазами и расплавом. Чтобы избежать влияния этого
фактора на все параметры равновесия (2.48), при поиске барических
коэффициентов мы фиксировали низкобарные
значения 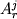 и и 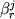 (Табл. 2.4)
и подбирали значения (Табл. 2.4)
и подбирали значения 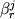 , наилучшим образом
описывающие зависимости температур ликвидуса
силикатов от давления. , наилучшим образом
описывающие зависимости температур ликвидуса
силикатов от давления.
В этой работе мы опирались на более
полные данные (Bender
et al., 1978 - Рис. 2.24), а результаты
(Green et al., 1979; Fujii,
Bougault, 1983) использовали для дополнительных
коррекций и контроля точности. При подборе
оптимальных значений барических коэффициентов
были постулированы одинаковые объемные
эффекты 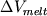 для Fo и Fa в Ol
(учитывая слабую зависимость для Fo и Fa в Ol
(учитывая слабую зависимость 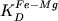 от
давления - Ford et al.,
1983) и соотношение от
давления - Ford et al.,
1983) и соотношение 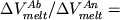 2:1,
отвечающее результатам термодинамического
анализа данных по равновесию Pl-расплав (Loomis, 1979). В
отношении авгита также предполагались
одинаковые объемные эффекты плавления для En,
Fs и Wo, тогда как в значение коэффициента
распределения Al (Табл. 2.4)
вводилась поправка, позволяющая учесть
обогащение клинопироксена Al2O3 на 0.5-0.7
мас.% при возрастании давления на 1 кбар (Арискин и др., 1991). 2:1,
отвечающее результатам термодинамического
анализа данных по равновесию Pl-расплав (Loomis, 1979). В
отношении авгита также предполагались
одинаковые объемные эффекты плавления для En,
Fs и Wo, тогда как в значение коэффициента
распределения Al (Табл. 2.4)
вводилась поправка, позволяющая учесть
обогащение клинопироксена Al2O3 на 0.5-0.7
мас.% при возрастании давления на 1 кбар (Арискин и др., 1991).
С 1993 г. модель КОМАГМАТ
включает следующие барические коэффициенты: 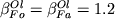 , , 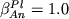 , , 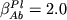 и
и 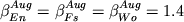 (Ariskin et al., 1993). Для
пижонита и ортопироксена
определить надежно эти параметры не удалось,
даже используя ряд новых данных, представленных
в системе ИНФОРЭКС-4.0: при
практических расчетах мы их варьируем в
диапазоне 1.4-1.8. Для Fe-Ti оксидов такие калибровки
не проводились. Тем не менее, этот простой подход
позволил в дальнейшем смоделировать главные
особенности полибарического
фракционирования толеитовых систем, связанные
с изменением поля устойчивости авгита
(Арискин и др., 1990,
1991). Воспроизводимость данных (Bender et al., 1978) при
использовании этой высокобарной модели показана
на Рис. 2.36, а результаты моделирования
полибарического фракционирования базальтовых
магм даны в Главах 4 и 5. (Ariskin et al., 1993). Для
пижонита и ортопироксена
определить надежно эти параметры не удалось,
даже используя ряд новых данных, представленных
в системе ИНФОРЭКС-4.0: при
практических расчетах мы их варьируем в
диапазоне 1.4-1.8. Для Fe-Ti оксидов такие калибровки
не проводились. Тем не менее, этот простой подход
позволил в дальнейшем смоделировать главные
особенности полибарического
фракционирования толеитовых систем, связанные
с изменением поля устойчивости авгита
(Арискин и др., 1990,
1991). Воспроизводимость данных (Bender et al., 1978) при
использовании этой высокобарной модели показана
на Рис. 2.36, а результаты моделирования
полибарического фракционирования базальтовых
магм даны в Главах 4 и 5.
Присутствие растворенной в
магматическом расплаве воды приводит к общему
понижению температуры ликвидуса,
изменению относительных полей устойчивости, пропорций кристаллизации и составов
минералов по сравнению с сухими условиями (Yoder, Tilley, 1962; Baker,
Eggler, 1983). С термодинамической точки зрения
это воздействие на фазовые равновесия
обусловлено влиянием воды на активность других
минералообразующих компонентов расплава, а
фактически проявляется в различной зависимости
температур кристаллизации минералов от
концентрации H2O в расплаве или давления
водосодержащего флюида - Рис. 2.25. Для учета этого
фактора в модели КОМАГМАТ нами
предложен простой эмпирический подход, который
пока не рассматривает всей сложности
взаимодействия воды с силикатными расплавами и
не учитывает конкретного механизма ее
растворения (Альмеев,
Арискин, 1996).
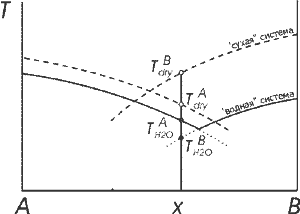
|
Рис. 2.25.
Схема ликвидусных отношений в бинарной
системе для сухих и водосодержащих условий
Рисунок показывает возможность
смены ликвидусных
фаз для расплава X при появлении в системе воды |
Этот подход включает разработку
эмпирического уравнения растворимости воды в
основных и кислых расплавах, оценку содержаний H2O
в водонасыщенных экспериментальных стеклах и
определение на этой основе поправочных
коэффициентов для расчета температур ликвидуса
породообразующих минералов при заданной
концентрации H2O в расплаве. Подстановка
этих коэффициентов в алгоритм расчета
равновесных температур кристаллизации
минералов (раздел 2.1) позволяет
в первом приближении учесть эффект влияния H2O
на фазовые равновесия, поскольку различие
поправочных коэффициентов для разных минералов
подразумевает изменение последовательности
появления минеральных фаз на ликвидусе при
переходе от сухих к водосодержащим условиям.
Эффект понижения температуры
ликвидуса минералов можно учесть путем
коррекции температур кристаллизации:
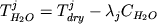 , (2.49) , (2.49)
где 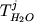 и и 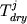 - температуры
появления j-минерала на ликвидусе в
водосодержащей и сухой системе; - температуры
появления j-минерала на ликвидусе в
водосодержащей и сухой системе; 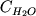 -
содержание воды в расплаве, а -
содержание воды в расплаве, а 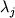 (оC/
мас.% H2O) - коэффициент пропорциональности,
который учитывает понижение температуры
ликвидуса для j-минерала, приходящееся на 1
мас.% H2O в расплаве. Значения коэффициентов (оC/
мас.% H2O) - коэффициент пропорциональности,
который учитывает понижение температуры
ликвидуса для j-минерала, приходящееся на 1
мас.% H2O в расплаве. Значения коэффициентов 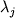 для оливина, плагиоклаза, авгита и низко-Ca
пироксена (главным образом - Opx) могут быть
рассчитаны исходя из экспериментальных данных
по фазовым равновесиям силикатных систем в
водонасыщенных условиях (Рис. 2.26): для оливина, плагиоклаза, авгита и низко-Ca
пироксена (главным образом - Opx) могут быть
рассчитаны исходя из экспериментальных данных
по фазовым равновесиям силикатных систем в
водонасыщенных условиях (Рис. 2.26):
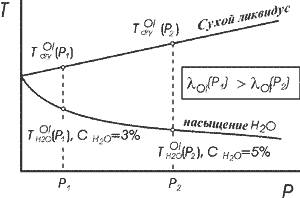
|
Рис. 2.26.
Схематичная P-T диаграмма
ликвидусных соотношений расплава гипо-
тетического оливинового базальта при
давлениях менее 10 кбар в сухих и водо-
насыщенных условиях
Рисунок проясняет смысл
коэффициентов
пропорциональности 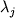 (2.50) (2.50)
на примере оливина |
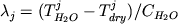 , (2.50) , (2.50)
где 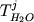 - экспериментальная
температура, - экспериментальная
температура, 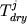 - температура кристаллизации j
минерала в сухих условиях, рассчитанная при
помощи геотермометров минерал-расплав
(Табл. 2.4), - температура кристаллизации j
минерала в сухих условиях, рассчитанная при
помощи геотермометров минерал-расплав
(Табл. 2.4), 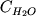 -
экспериментально замеренное или рассчитанное
содержание H2O в закалочном стекле (мас.%). -
экспериментально замеренное или рассчитанное
содержание H2O в закалочном стекле (мас.%).
Обработав таким образом серию данных
по расплавным равновесиям с участием данного
минерала, можно рассчитать средние значения 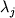 (Арискин и др.,
1995). Рассчитанные коэффициенты можно затем
разделить на несколько групп, отвечающих
различным давлениям, и попытаться установить
зависимость (Арискин и др.,
1995). Рассчитанные коэффициенты можно затем
разделить на несколько групп, отвечающих
различным давлениям, и попытаться установить
зависимость 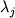 от P (Альмеев, Арискин,
1996). от P (Альмеев, Арискин,
1996).
Для решения этих вопросов мы
использовали информацию, представленную в
системе ИНФОРЭКС-4.0 (1997) - см. Рис.
2.8. База данных включает
более 2000 экспериментов, проведенных в
водонасыщенных условиях. Эти исследования
проводились с природными образцами (базальты,
андезиты, дациты, риолиты) и синтетическими
смесями в условиях избытка H2O при
температурах 675 < T < 1300оС,
давлениях 100 бар < P < 30 кбар и
продолжительности опытов от 1 до 800 часов.
Примерно в 500 случаях имеются данные по составам
закаленных стекол; в ряде случаев приведены
составы равновесных минеральных фаз. Проблема
использования этой информации для оценки
влияния воды на температуры кристаллизации (2.50) осложняется тем, что для
большинства опытов не известна концентрация H2O
в расплавах, отвечающих условию
насыщения (присутствию равновесной паровой
фазы). В этой связи решающее значение приобретает
поиск функциональной зависимости, позволяющей
максимально точно предсказывать растворимость
воды в силикатной жидкости.
Оценки растворимости воды в расплаве.
Эта задача была решена путем построения
эмпирического уравнения, основанного на
результатах обработки немногочисленных прямых
данных о растворимости воды в силикатных
расплавах (Альмеев,
Арискин, 1996):
![$\ln C_{H_2 O} = 4.39 + [38483(Si/O)^l - 14710]/T + 0.59\ln P - 21.45(Si/O)^l + 3.89(Al/Si)^l$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula138.gif) , (2.51) , (2.51)
где температура выражена в градусах
Кельвина, давление в барах, а параметры расплава
в атомных единицах.
Уравнение (2.51) калибровано на данных 79
экспериментов, проведенных в области
двухфазного равновесия расплав-пар в интервале
давлений 200 бар - 9 кбар и температур 800-1200оC (Hamilton et al., 1964; Кадик и др., 1971; Sisson, Grove, 1993; Dixon et al.,
1995). Сравнение расчетных и экспериментальных
значений растворимости H2O в расплавах
показывает, что уравнение (2.51)
воспроизводит экспериментальные данные с
погрешностью порядка 0.3 мас.% и может быть
использовано для расчета растворимости H2O
при давлениях до 10 кбар (Альмеев, Арискин,
1996).
Расчет поправочных коэффициентов 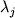 . Используя поисковую процедуру системы
ИНФОРЭКС-4.0, из общего числа
водонасыщенных экспериментов были отобраны
опыты, проведенные с образцами лерцолитов,
базальтов и андезитов
при давлениях до 10 кбар. Представленные в этих
опытах составы закалочных стекол
были сгруппированы по признаку присутствия
конкретного минерала в составе равновесной с
расплавом ассоциации (например, в случае оливина - Ol+l, Ol+Pl+l, Ol+Aug+Pl+l и
т.д.). Таким образом были сформированы четыре
массива данных: Ol-расплав (69 опытов), Pl-расплав
(81), Aug-расплав (56) и Opx-расплав (19). . Используя поисковую процедуру системы
ИНФОРЭКС-4.0, из общего числа
водонасыщенных экспериментов были отобраны
опыты, проведенные с образцами лерцолитов,
базальтов и андезитов
при давлениях до 10 кбар. Представленные в этих
опытах составы закалочных стекол
были сгруппированы по признаку присутствия
конкретного минерала в составе равновесной с
расплавом ассоциации (например, в случае оливина - Ol+l, Ol+Pl+l, Ol+Aug+Pl+l и
т.д.). Таким образом были сформированы четыре
массива данных: Ol-расплав (69 опытов), Pl-расплав
(81), Aug-расплав (56) и Opx-расплав (19).
Для составов закалочных стекол
каждого из четырех массивов данных с помощью
программного комплекса КОМАГМАТ
при заданных давлениях были рассчитаны
температуры кристаллизации в безводных условиях
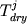 ; полученные значения оказались на 100-300oC
выше экспериментальных температур ; полученные значения оказались на 100-300oC
выше экспериментальных температур 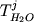 .
Далее, для каждого опыта разница .
Далее, для каждого опыта разница 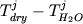 была нормирована на концентрацию H2O в
расплаве, рассчитанную при помощи уравнения (2.51). Определенные таким
образом средние значения
степени понижения температур кристаллизации
была нормирована на концентрацию H2O в
расплаве, рассчитанную при помощи уравнения (2.51). Определенные таким
образом средние значения
степени понижения температур кристаллизации
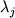 для оливина, плагиоклаза, авгита и
ортопироксена в зависимости от давления для оливина, плагиоклаза, авгита и
ортопироксена в зависимости от давления 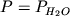 представлены в Табл. 2.5.
представлены в Табл. 2.5.
Таблица 2.5.
Значение поправочных коэффициентов 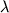 при
различных давлениях. при
различных давлениях.
P, кбар |
Ol |
Aug |
Opx |
Pl |
1 |
17.9  6.0 (14) 6.0 (14) |
34.3  7.1 (12) 7.1 (12) |
22.4  3.4 (2) 3.4 (2) |
59.6  7.8 (23) 7.8 (23) |
2 |
18.7  2.9 (21) 2.9 (21) |
24.8  2.2 (19) 2.2 (19) |
22.3  1.2 (4) 1.2 (4) |
49.9  4.2 (18) 4.2 (18) |
2.5 |
|
23.7  3.9 (3) 3.9 (3) |
|
47.6  1.0 (3) 1.0 (3) |
3 |
|
|
18.3 (1) |
43.1  1.5 (23) 1.5 (23) |
4 |
|
|
|
38.3  1.6 (3) 1.6 (3) |
5 |
10.2  5.5 (3) 5.5 (3) |
15.5  3.3 (8) 3.3 (8) |
|
38.1  3.1 (6) 3.1 (6) |
6.9 |
|
|
|
37.8  0.6 (5) 0.6 (5) |
7.5 |
5.1  3.7 (3) 3.7 (3) |
14.5  1.6 (4) 1.6 (4) |
12.5  2.2 (4) 2.2 (4) |
|
10 |
1.3  0.7 (2) 0.7 (2) |
10.5  1.1 (5) 1.1 (5) |
9.3  1.0 (4) 1.0 (4) |
|
| Примечание. В
скобках - число точек. |
При разработке первой "водной"
версии модели КОМАГМАТ мы использовали
средние значения 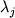 , которые не зависели от
давления: для Pl - 42.2, Ol - 17.5, Aug - 27.4 и Opx
- 22.4 оС/ %H2O (Арискин и др., 1995). , которые не зависели от
давления: для Pl - 42.2, Ol - 17.5, Aug - 27.4 и Opx
- 22.4 оС/ %H2O (Арискин и др., 1995).
Особенность поведения микроэлементов
в магматических системах состоит в том, что при
содержаниях в расплаве 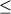 0.1-0.2 мас.% они
практически не оказывают влияние на фазовые
равновесия главных породообразующих минералов.
Определенное исключение составляет лишь Cr, от
концентрации которого зависит устойчивость и
появление на ликвидусе шпинелида
(Hill, Roeder, 1974). В
этом смысле задача распределения микроэлементов
в системе кристалл - расплав может быть отделена
от решения задачи равновесия по главным
элементам и рассматриваться после того, как
определены (рассчитаны) пропорции твердых фаз и
расплава. 0.1-0.2 мас.% они
практически не оказывают влияние на фазовые
равновесия главных породообразующих минералов.
Определенное исключение составляет лишь Cr, от
концентрации которого зависит устойчивость и
появление на ликвидусе шпинелида
(Hill, Roeder, 1974). В
этом смысле задача распределения микроэлементов
в системе кристалл - расплав может быть отделена
от решения задачи равновесия по главным
элементам и рассматриваться после того, как
определены (рассчитаны) пропорции твердых фаз и
расплава.
Традиционный подход к описанию
разделения микроэлементов между минералами и
расплавом связан с использованием весовых
коэффициентов распределения
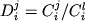 , (2.52) , (2.52)
где концентрации i-го элемента в
минерале j и расплаве даны в мас.% или ppm.
Это чисто эмпирический параметр, который может
быть рассчитан по составам экспериментально
синтезированных кристаллов и закалочных
стекол (Irving, 1978)
или данных природных наблюдений,
характеризующих "равновесия" фенокристалл
- матрица и минерал-хозяин - расплавное
включение (Соболев
и др., 1996). Существуют и косвенные методы
оценок значений 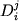 , основанные на моделях
поведения микроэлементов при дифференциации
базальтовых магм, например (Кравченко, 1977; Бармина
и др., 1982). , основанные на моделях
поведения микроэлементов при дифференциации
базальтовых магм, например (Кравченко, 1977; Бармина
и др., 1982).
В действительности, выбор
эмпирического базиса для построения моделей
фракционирования микроэлементов не столь
очевиден. Дело в том, что большинство
экспериментальных данных о распределении
элементов-примесей получены в системах,
искусственно дозированных тем или иным
микроэлементом. Это вызывает необходимость
решения вопроса о том, можно ли использовать при
термодинамическом моделировании коэффициенты
распределения, замеренные в области
концентраций, существенно превышающей их
природные содержания. К счастью, специальные
исследования проблемы выполнимости закона
Генри показали, что для большинства
микроэлементов зависимость (2.52)
выполняется в широких пределах, включающих
диапазон природных концентраций - см. обзор в
работе (Френкель и
др., 1988).
Выполнение закона Генри
для коэффициентов распределения (2.52) указывает на то, что
поведение микроэлементов в системе твердая фаза
- расплав подчиняется законам термодинамики
и может быть описано в терминах зависимости свободной энергии образования
микрокомпонентов минерала от температуры,
давления и состава системы: см., например,
уравнения (1.20-1.24), где MgO может быть
заменен на Ni, Mn или Co. Такого рода попытки
предпринимались неоднократно (здесь можно особо
отметить работы Нильсена с коллегами), однако
единого и систематического подхода к описанию
распределения микроэлементов до сих пор не
разработано. В значительной мере это связано с
необходимостью корректного описания активности
микрокомпонентов в расплаве и минералах - эти
проблемы ждут своего решения.
Таким образом, в моделях серии КОМАГМАТ мы используем
фиксированные значения или
температурно-композиционные зависимости весовых
коэффициентов распределения (2.52), большинство из которых
рассчитано по результатам экспериментальных
исследований фазовых равновесий синтетических и
природных силикатных систем. В процессе
ЭВМ-моделирования программа КОМАГМАТ
позволяет рассчитывать эволюцию содержаний для
20 микроэлементов, которые разделены на две
группы: (1) Mn, Ni, Co, Cr, Sc, V, Sr, Ba, Rb, Cu и (2) редкоземельные
элементы, включающие La, Ce, Nd, Sm, Eu, Gd, Dy, Er, Lu, Yb.
Первая группа (Mn, Ni, Co, Cr, Sc, V, Sr, Ba, Rb, Cu).
Данные для элементов этой группы были
систематизированы и обработаны нами в конце 80-х
годов (Френкель и др.,
1988). Принятые значения и температурные
зависимости приведены в Табл. 2.6 и Табл. 2.7.
Табл. 2.6. Коэффициенты
распределения минерал-расплав для
микроэлементов первой группы
| |
Mn |
Ni |
Co |
Cr |
Sc |
V |
Sr |
Ba |
Rb |
Cu |
Pl |
(0.03) |
(0.03) |
(0.03) |
(0.03) |
(0.03) |
(0.03) |
ТЗ |
ТЗ |
0.20 |
(0.03) |
Ol |
ТЗ |
ТЗ |
ТЗ |
0.90 |
0.37 |
(.004) |
(.004) |
(.004) |
(.004) |
(0.05) |
Aug |
ТЗ |
6.0 |
3.0 |
(10.0) |
2.5 |
1.5 |
0.22 |
0.10 |
0.10 |
(0.05) |
Pig (Opx) |
(1.0) |
3.0 |
1.6 |
3.0 |
(1.0) |
(1.0) |
0.02 |
(0.01) |
(0.01) |
(0.05) |
Ilm |
(1.0) |
10.0 |
5.0 |
10.0 |
.50 |
10.0 |
(0.01) |
(0.01) |
(0.01) |
(1.0) |
Mt |
(2.0) |
29.0 |
7.4 |
50.0 |
2.50 |
26.0 |
(0.01) |
(0.01) |
(0.01) |
(1.0) |
Примечания. ТЗ - температурные
зависимости (см. Табл. 2.7). Значения в скобках
указывают, что это ориентировочные параметры,
небольшие вариации которых не приводят к
существенным изменениям рассчитанных
эволюционных линий.
Табл. 2.7.
Температурные зависимости коэффициентов
распределения минерал-расплав для
микроэлементов первой группы
Вторая группа (La, Ce, Nd, Sm, Eu, Gd, Dy, Er, Lu, Yb).
Температурно-композиционные и барические
зависимости для коэффициентов распределения
редкоземельных элементов опубликованы в работе (Бармина и др., 1991).
Данные для обработки включали более 200
экспериментальных значений 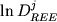 , полученных
в период 1974-1988 гг. На основании этой информации
для Ol, Pl, Aug, Opx и Ilm были
рассчитаны эмпирические уравнения вида , полученных
в период 1974-1988 гг. На основании этой информации
для Ol, Pl, Aug, Opx и Ilm были
рассчитаны эмпирические уравнения вида
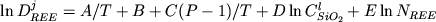 , (2.53) , (2.53)
где T - температура (оK), P
- давление (бар), 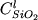 - содержание SiO2 в
расплаве (мас.%), - содержание SiO2 в
расплаве (мас.%), 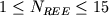 - порядковый номер
редкоземельного элемента от La до Lu, A, B, C, D и E
- регрессионные коэффициенты. При проведении
этих вычислений было получено по две зависимости
для каждого минерала - одна для легких и
другая для тяжелых РЗЭ; при этом в
качестве элемента разделителя использовался Gd.
Это позволило учесть известный эффект наличия
максимума значений - порядковый номер
редкоземельного элемента от La до Lu, A, B, C, D и E
- регрессионные коэффициенты. При проведении
этих вычислений было получено по две зависимости
для каждого минерала - одна для легких и
другая для тяжелых РЗЭ; при этом в
качестве элемента разделителя использовался Gd.
Это позволило учесть известный эффект наличия
максимума значений 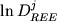 для авгита,
приходящегося на Dy и Gd, и при расчетах
моделировать эволюцию полных спектров
редкоземельных элементов (Бармина и др., 1991).
Соответствующие регрессионные параметры
приведены в Табл. 2.8. для авгита,
приходящегося на Dy и Gd, и при расчетах
моделировать эволюцию полных спектров
редкоземельных элементов (Бармина и др., 1991).
Соответствующие регрессионные параметры
приведены в Табл. 2.8.
Для коэффициентов распределения Eu
между Aug, Pl и расплавом мы использовали
дополнительные зависимости от летучести
кислорода, рассчитанные по данным (Sun et al., 1974; Drake,
1975) - см. Табл. 2.7. При расчетах фазовых
равновесий с участием пижонита и магнетита постулировалось, что 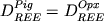 и и 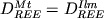 . .
Табл. 2.8. Параметры
температурно-композиционых зависимостей
коэффициентов распределения минерал-расплав для
редкоземельных элементов (2.53)
Группа |
Условия опытов |
Регрессионные
коэффициенты |
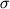 (n) (n)
|
РЗЭ |
T, oC |
P, кбар |
A |
B |
C |
D |
E |
|
П л а г и о к л а з |
ЛРЗЭ |
1150- |
0.001 |
4575 |
-1.63 |
- |
-0.78 |
-0.49 |
0.18 (65) |
ТРЗЭ |
1343 |
|
-6951 |
-11.37 |
- |
3.50 |
-0.56 |
0.22 (35) |
О л и в и н |
ЛРЗЭ |
1150- |
0.001 |
17054 |
-51.20 |
- |
8.24 |
1.08 |
0.41 (22) |
ТРЗЭ |
1414 |
|
12473 |
-37.01 |
- |
4.07 |
3.54 |
0.26 (38) |
А в г и т |
ЛРЗЭ |
1050- |
7.5-30 |
5432 |
1.70 |
0.04 |
-1.79 |
0.34 |
0.25 (16) |
ТРЗЭ |
1380 |
7.5-20 |
-800 |
-9.12 |
0.15 |
2.52 |
-0.31 |
0.16 (27) |
О р т о п и р о к с е н |
ЛРЗЭ |
1169- |
0.001 |
21891 |
-19.63 |
- |
- |
0.67 |
0.38 (9) |
ТРЗЭ |
1414 |
|
22995 |
-24.29 |
- |
- |
2.62 |
0.22 (13) |
И л ь м е н и т |
ЛРЗЭ |
1122- |
0.001 |
- |
-5.73 |
- |
- |
0.24 |
0.78 (11) |
ТРЗЭ |
1157 |
|
- |
-14.25 |
- |
- |
4.30 |
0.19 (10) |
Примечания. ЛРЗЭ и ТРЗЭ - легкие и
тяжелые редкоземельные элементы; 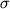 - среднеквадратичные
отклонения величины - среднеквадратичные
отклонения величины 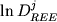 при решении
обратной задачи (в скобках - число точек). при решении
обратной задачи (в скобках - число точек).
Расчет распределения микроэлементов между
фазами системы в модели КОМАГМАТ
производится в блоке ИНФОРМ
после определения равновесных количеств
минералов 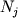 при заданном количестве расплава при заданном количестве расплава 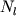 (Рис. 2.2). При этом молекулярные
количества минералов и расплава
пересчитываются на весовые -
(Рис. 2.2). При этом молекулярные
количества минералов и расплава
пересчитываются на весовые - 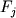 и и 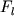 , а
содержания микроэлементов в
расплаве и минералах вычисляются при помощи
уравнений баланса
масс: , а
содержания микроэлементов в
расплаве и минералах вычисляются при помощи
уравнений баланса
масс:
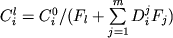 и и 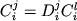 , (2.54) , (2.54)
где 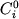 - общее содержание i-го
микроэлемента в исходной системе. - общее содержание i-го
микроэлемента в исходной системе.
Опыт последующей работы с
программой КОМАГМАТ показал, что
рассмотренные параметры распределения
микроэлементов позволяют реалистично
предсказывать их поведение в магматическом
процессе и даже использовать при оценках
термодинамических и динамических параметров
фракционирования магм (см. Главу 3). Это
обусловлено не только удачным выбором значений 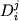 , но также спецификой кристаллизационных
процессов, которые протекают в условиях, когда
количество расплава преобладает или соизмеримо
с количеством взвешенного в магме
кристаллического материала. Это отвечает
условиям проведения экспериментов, направленных
на достижение однородного (равновесного)
распределения элементов между фазами системы.
, но также спецификой кристаллизационных
процессов, которые протекают в условиях, когда
количество расплава преобладает или соизмеримо
с количеством взвешенного в магме
кристаллического материала. Это отвечает
условиям проведения экспериментов, направленных
на достижение однородного (равновесного)
распределения элементов между фазами системы.
Назад | Оглавление|
Далее
Примечания:
11 Эмпирическая модель Боттинга и Вейла была предложена для описания зависимости вязкости природных силикатных расплавов от температуры и состава. Эта модель предполагает, что тетраэдрически координированные ионы Al3+ в расплаве ассоциированы с катионами металлов, порядок предпочтения которых - K+ > Na+ > Ca2+ > Mg2+ > Fe2+. Это приводит к образованию "молекул" вида KAlO2, NaAlO2, CaAl2O4; в случае дефицита алюминия относительный избыток кальция и щелочей пересчитывался на компоненты
CaO, Na2O и K2O.
12 Здесь были даны калибровки геотермометров минерал-расплав, описывающие равновесия с участием оливина, плагиоклаза, пироксенов, ильменита и шпинелидов.
|

