 |
|
 |
|
What the geoscientist might really like to do is to cut the Earth along a line, down some thousands of meters, and have a look at the rocks, and their pore fluid, in place. While this rather invasive technique is not yet popular, analogous methods are. Seismic tomography (ST) is a means of making a picture of a slice of the earth using seismic data.
Methods to construct images of an object from "projections" of x-rays, ultrasound or electromagnetic waves have found wide applications in electron microscopy, diagnostic medicine and radio astronomy. Projections are measurable quantities that are a functional – usually involving a line integral – of physical properties of an object. Convolutional methods or iterative algorithms to solve large systems of linear equations are used to reconstruct the object. In principle, there is no reason why similar image reconstructions can not be made with seismic waves.
The idea of global tomogrphy study is that the travel-time anomalies observed for many ray paths, criss-crossing the Earth between various points near the Earth's surface and reaching different depths in its interior, could be resolved formally into a 3-D model. The motivation for studying 3-D structure of the Earth's interior is that it may offer the best information on the dynamic processes in the deep interior of the Earth.
Tomography is a type of inverse problem. That is, measurements are first made of some energy that has propagated through a medium. The received character of this energy (e.g., amplitude, travel-time) is then used to infer the values (e.g., velocity, density, permittivity) of the medium through which it has propagated.
The tomographic problem can be stated as: "From projections (sums of some interior value) measured outside of an object find the interior distribution of values inside the object." A projection is the sum of an object's parameters along a given linear energy transit path. A sum or integral of this type is also known as a Radon transform [4].
The Radon transform is the forward part of the tomographic problem. Then, in the tomographic procedure, we must take these projections and create an image from them. There are two broad categories of techniques used to infer the medium's internal values from the projections. They are "transform" and "series expansion" methods.
Transform techniques
Transform methods start with the motion of an object being described by a continuous function, with a continuous set of projections. There are two main transform methods: the Fourier techniques and the filtered backprojection method.
The Fourier projection theorem states that the 2-D (3-D) Fourier transform of an image or medium can be obtained form the 1-D (2-D) Fourier transforms of the projections. [5] Thus, by measuring the projection of the object and constructing the 2-D (3-D) transform space accordingly, then inverse 2-D (3-D) Fourier transforming, an image of the object may be reconstructed. A major difficulty with this reconstruction is that it requires a complete (all the way around the objects) set of projections.
Backprojection is an operation which sums projected values (Radon transforms) together. The basic idea is that each point that is traversed by the ray from the source to receiver is given the value of the total projection. The image is built up by summing all the values of the points determined for every ray.
This backprojection method can be used to create images, but it is one that leads to blurring of the final reconstructed image. To attain a better image, it is reasonable to attempt a spatial deconvolution. This method is called "filtered backprojection", the notion arising of filtering the backprojection to provide a clearer image.
In the above discussion, it has been assumed that energy propagates as a ray (i.e. by infinitely thin beams in straight lines). However, elastic or acoustic waves have well known properties of divergence and diffraction in accordance with the wave equation. It is nonetheless possible to build wave equation propagation into a tomographic framework. This method is called "diffraction tomography" (DT) [7, 8]. Examples of DT inversion methods are "filtered backpropogation algorithms" [6].
Series Expansion Methods
The series expansion methods start by considering the object or area of interest to be comprised of boxes or pixels. Energy is considered to propagate through the various pixels to provide a sum or projection of the pixel values. The pixel values are now related to the sum. This is often related to solving large linear equations. A stable but approximate solution, as discussed previously, is known as backprojection. In the matrix formulation backprojection corresponds to using the transpose of matrix instead of the inverse. Two other more accurate but iterative methods are known as ART (Algebraic Reconstruction Technique) and SIRT (Simultaneous Iterative Reconstruction Technique) [5].
We can consider the whole 3-D earth as an object to be imaged in a manner similar to the medical case. That is, we imagine sources and receivers distributed around the Earth and a survey performed. In this geophysical case though, the sources are major earthquakes or large explosions and the receivers are geophones or accelerometers. Figure 1 shows that seismic tomography attempts to find velocity anomalies by combining information from many seismic waves traveling from earthquakes (circle and dot) to seismic stations (black dot) along criss-crossing paths [5]. Seismic energy travels through the Earth and is recorded by a distribution of receivers. By picking the arrival times of the propagating energy for a number of earthquakes and stations, a velocity model of the earth can be reconstructed. Likewise, by measuring the amplitudes of the arriving events, a seismic attenuation structure of the earth can be inferred.
Global images of the Earth's interior
The first major global tomographic study was made by Professor Dziewonski et al [2]. In early 70's, using the data set of nearly 100 digitized seismograms of the Alaskan earthquake, they detected and measured frequencies of many previously unidentified modes of free vibrations of the earth, corrected some of the earlier mis-identifications and, generally, significantly improve the overall accuracy of the entire data set. An immediate reward was the ability to present a satisfactory proof that the inner core of the earth is solid [1].
Attempts to reproduce the observed seismograms using the average earth structure and the seismic source led them to progress from one to three dimensions. They got some success for shallow structure (the crust and the top several hundred kilometers) first, then the same was applied to the lower mantle (700-2900 km depth) [1]. Dziewonski recognized the potential of the ISC (International Seismological Center) data set. They used 700, 000 P wave travel time residuals to determine some 150 coefficients of a spherical harmonic expansion of velocity perturbations in the Earth's mantle by means of a least-squares analysis [3]. In his later attempt, he determined spherical harmonic coefficients up to degree 6 [10]. A lasting result of the late 1970's was reference earth model.
The progress in digital seismology and, in particular, global deployment of highly sensitive seismometers, made it possible to apply inversion of seismic waveform data for the moment tensor not only to great earthquakes, but also to much more numerous smaller events. Dziewonski and John Woodhouse [9] used CMT (centroid-moment tensor) technique to improve the knowledge of the 3-D structure of the mantle [1]. Then, to complete this first sweep through the earth's interior, they investigated the velocity variation of the core-mantle boundary and the properties of the inner core ( figure 2 &3 ).
As the result, a consensus was developing on a series of issues [11]:
Their current tomographic studies move towards the resolution of tomographic models [1].
Imaging 3-D spherical convection models
Charles Mégnin et al. assessed whether current global seismic tomography can resolve parameters characterizing mantle dynamics, in particular 1) a viscosity increase from the upper to the lower mantle, 2) an endothermic phase transition at the 670 km discontinuity, 3) eat flux across the core-mantle boundary and 4) the effect of the motion of rigid surface plates on the convection platform. They applied a 'linear seismic filter' to numerical convection models that incorporate the desired physical parameter.
Their results indicated that tomography can resolve characteristic signatures of input convection models. Comparison with actual 3-D seismic mantle models indicated that the effect of rigid plates dominates the spectral characteristics of the models.
Imaging 3-D lithospheric structure using micro-earthquakes
New seismic techniques, utilizing signals from the large numbers of micro-earthquakes occurring in tectonically active areas, can now provide detailed 3-D seismic velocity structure images and 3-D "maps" describing on-going tectonic deformation [13]. The deformation is expressed in terms of spatial variations in the magnitude of the stress released by micro-earthquake fracturing, the spatial variations in total strain energy release by brittle fracture and also in terms of the 3-D determination of the energy release levels from rapid creep deformation along faults. Taken together, the seismic velocity structure and the spatial definition of the tectonic state of the medium can be used to characterize the physical properties of the material and its deformational strain state and to define the large scale faulting dynamics within the medium.
Building a high-resolution seismic model
A team of seismologists has used a cluster of four IBM RS/6000s to create a detailed 3D model of the faults and structures under California's shaky San Francisco Bay Area [14]. Kevin P. Furlong, a professor of geosciences and Pennsylvania State University, and his team, combined earthquake data collected over the past 25 years with acoustic soundings from a 1991 experiment to determine the structures and materials as deep as 12 kilometers in the earth's crust.
To gather data about the rock structure below the surface, seismologists use the time it takes for energy to travel form an earthquake or an artificial sound source to seismic receivers deployed throughout an area. According to Furlong, "through a 3D inversion of these travel times we can develop a 3D view of the seismic velocity characteristics of the crust." From that data, the researchers can interpret the types of rocks in the crust and the 3D structure of the rock bodies. To do so, they used finite difference programs that calculated travel times form sources to receivers.
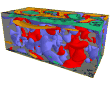
Furlong and his team started with a blank slate of sorts, a 3D model of the structure in which, at any given depth, rock structures are homogenous, yielding equal travel times for equal distances. The actual rock structures are much more complex, composed of different tock types, faults, and fissures, and yielding different travel times. As they entered travel times, a view of the underground structure began to appear ( figure 4 [14]). They refined the model by iteratively calculating it based on the waves' travel times.
Their study proved that the degree of complexity observed at the surface continues throughout the upper and lower crust ( figure 5 [14]). They have identified features in the middle crust that might help to measure how far faults have moved, and they have mapped sedimentary basins throughout the region – all aspects of improving understanding of earthquakes in the area.
Tomography techniques have been used with great success in medical imaging. With more exposure of tomographic ideas to the geophysical community and more complete field acquisition, tomographic theory for the seismic case is being developed and applied. In particular, ST is being successfully used to provide structural velocity models, rock attenuation models, more accurate depth migrations, calibrated seismic inversion sections, high-resolution crosswell pictures, and 3-D Earth images.
3-D images of the earth's interior are having a large impact on the understanding of the structure and dynamics of the planet. Whole Earth reconstructions are tremendously exciting and useful images. More regional tomograms can be reconstructed using smaller earthquakes and local networks. These images are very helpful to understand Earth structure.
[1] Dziewonski
Website
[2] Harvard
3-D tomography
[3] Guust Nolet (Ed.), 1986, Seismic tomography, with applications in global
seismology and exploration geophysics, D. Reidel publishing company.
[4] Natterer, F., 1986, The mathematics of computerized tomography, J. Wiley
and Sons Ltd., and B.G. Teubner.
[5] Robert R. Stewart, 1991, Exploration seismic tomography: fundamentals,
Course notes series, Volume3.
6] Devaney A.J., 1982, A filtered backpropogation algorithm for diffraction
tomography, Ultrasonic Imaging, 4, 336-50.
[7] Devaney A. J., 1984, Geophysical diffraction tomography, IEEE trans.
on Geosci. And Remote Sensing GE-22, 3-13.
[8] Witten A. J. &Molyneux J.E., 1992, Geophysical diffraction tomography:
validity and implementation, Geophysical Inversion, eds Bednar J.B., Lines
L.R., Stolt R.H. and Weglein A.B. (SIAM) 354-69.
[9] Dziewonski A. M., &Woodhouse J. H., 1987, Global images of the Earth's
interior, Science, 236, 37-48.
[10] Dziewonski A. M., 1984, Mapping the lower mantle: determination of
lateral heterogeneity in P velocity up to degree and order 6, J. Geophys.
Res., 89, 5929-5852.
[11] Dziewonski A. M., 1993, Tomographic image of the Earth interior; a
review, Eos, transactions, American geophysical Union, 74; 43, Suppl., pages
572, 1993.
[12] Charles Mégnin, Hans-Peter Bunge, Barbara Romanowicz and Mark
A. Richards, Imaging 3-D spherical convection models: What can seismic tomograph
tell us about mantle dynamics?, Geohpysical research letters, Vol. 24, No.
11, Pages 1299-1302, June 1, 1997.
[13] Charles Archambeau, and Benjamin Kohl, Imaging three dimensional lithospheric
structure using micro-earthquakes: High resolution seismic tomography, Global
Tectonics and Metallogeny, Vol. 6, No. 2, 1997.
[14] Dave Sims, Biuilding a high-resolution seismic model, IEEE Computer
Graphics, Vol. 15, No. 4, Pages 16-17, July 1995. [15] Penn
State Geodynamics