Влияние граничных эффектов на состав расплавных включений: эксперимент и моделирование.

П. Ю. Плечов, С. В. Трусов (МГУ, геологический факультет)

Ключевые слова: [расплавные включения, диффузия, граничныйе эффекты]

Введение.
Хорошо известно, что состав расплава вблизи поверхности растущего кристалла отличается от валового состава расплава вследствие граничных эффектов перераспределения вещества между расплавом и кристаллом. Наблюдаемая ширина этого слоя колеблется в зависимости от вязкости расплава и условий роста кристалла от 10-15 (для маловязких базальтовых расплавов) до 100-150 микрон (для риолитовых расплавов). Учитывая, что расплавные включения формируются из участка расплава, непосредственно примыкающего к растущему кристаллу, логично предположить, что их состав также будет искажен по сравнению с валовым составом расплава. Smith и др. [3] первыми показали, что расплав в граничном слое должен быть обеднен совместимыми компонентами и обогащен несовместимыми.

Экспериментальное получение граничных эффектов
Для определения влияния граничных эффектов на состав расплавных включений был поставлен эксперимент по росту кристаллов щелочного полевого шпата (Fsp) в гаплогранитной системе (Q-Ab-Or). Система охлаждалась 6 суток с 760 до 700 ^oС со скоростью 10^o/сут, после чего закаливалась. В результате были получены диффузионные профили возле кристаллов Fsp, которые приведены на рис. 1. На этих профилях хорошо видны эффекты обогащения граничного слоя, примыкающего к кристаллу, теми компонентами, которых меньше в Fsp, чем в расплаве (например, SiO₂). Однако, на участке профиля через граничный слой, удаленном от поверхности кристалла, фиксируется обеднение SiO₂ и обогащение Al₂O₃. Этот эффект труднообъясним простой диффузионной отгонкой компонентов от растущей грани.

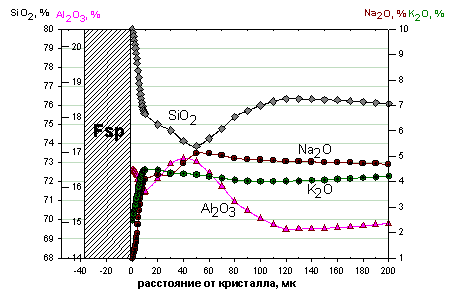Рис1. Распределение компонентов расплава на границе с растущим кристаллом полевого шпата

Компьютерное моделирование граничных эффектов
Авторами проводилось компьютерное моделирование роста кристалла Fsp в гранитном расплаве. При этом было использовано уравнение многокомпонентной диффузии и алгоритм Oishi [2] для численного расчета. Рост кристалла моделировался по механизму послойного роста. Коэффициенты диффузии компонентов были взяты из работ [1,4]. Основной сложностью было моделирование той части профиля, которая удалена от растущей грани. Конфигурация профиля (рис. 1) предполагает встречные диффузионные потоки, которые переносят одни и те же компоненты в противоположные стороны. Это означает, что эти компоненты должны находиться в расплаве в различных по составу частицах. При этом, направленный к кристаллу поток частиц должен вычерпываться растущей гранью, чтобы создавался градиент концентраций. Предположение о том, что перенос компонентов к растущей грани осуществляется частицами состава растущего минерала, позволил нам добиться удовлетворительных результатов моделирования, сходных с экспериментальными профилями.

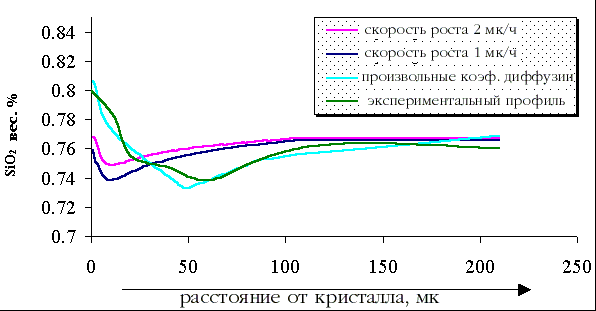Рис.1a. Моделирование граничных эффектов при росте полевого шпата

На рис. 1а изображены две рассчитанные кривые диффузионной подвижности кремнезема при росте Fsp со скоростями 1 и 2 мк/час и одна кривая рассчитанная с переменными коэффициентами диффузии (введена зависимость коэффициентов диффузии от концентрации компонентов). Следует отметить, что расчетные диффузионные профили нестационарны во времени и представляют собой колебательную систему (период колебаний зависит от частоты образования новых слоев). Неопределенность многих параметров, таких как коэффициенты диффузии комплексов в расплаве, их размеры, химическое взаимодействие между этими комплексами и т.п. не позволяют на сегодняшний день создать полную количественную модель этого процесса.

Оценка влияния граничных эффектов на состав расплавных включений

Если предположить, что расплавные включения при формировании частично захватывают граничный слой, то состав малых включений должен отвечать среднему составу захваченной части граничного слоя. Чем больше включение, тем меньшее влияние на его состав оказывает граничный слой.

На рис. 2 показаны рассчитанные кривые среднего состава граничного слоя в зависимости от размера включения. Точками на этой диаграмме показаны составы расплавных включений, имеющих диаметр, соответствующий размерности оси Х. В основном, наблюдается хорошая корреляция между предсказанными и померенными составами расплавных включений.

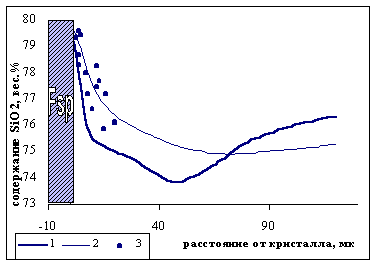Рис.2. Распределение кремнезема на границе с растущим кристаллом полевого шпата (Fsp). 1 √ экспериментальный дмффузионный профиль, 2 √ интегральный профиль, 3 - содержание кремнезема в распавных включениях в Fsp

Таким образом, с помощью исследования диффузионных профилей появляется возможность рассчитать поправку к составам расплавных включений. Теоретическое моделирование роста кристаллов в синтетических системах репродуцирует экспериментальные профили через граничный слой и может быть использовано для предсказания состава расплавных включений.

Литература

1. Чехмир А.С., Симакин А.Г., Эпельбаум М.Б. (1991) "Динамические явления во флюидно - магматических системах" М.: Наука, 141стр.
2. Oishi Y. (1965). "Analysis of ternary diffusion: solutions of diffusion equations and calculated concentration distribution." J. Chem. Phys. 43(5): 1611-1620.
3. Smith V. G., Tiller W. A., et al. (1955). "A mathematical analysis of solute redistribution during solidification." Can. J. Phys. 33: 723-744.
4. Watson, E. B. and D. R. Baker (1991). Chemical diffusion in magmas: an overview of experimental results and geochemical applications (chapter 4).Physical chemistry of magmas. L. L. Perchuk and I. Kushiro. New York, Berlin, London, Paris, Tokyo, Hong-Kong, Barselona, Springer-Verlag. 9: 352 pp. (p.120-151 - for chapter 4).