Next: 2.2. Криптография и гипотеза
Up: 2. Криптография и теория
Previous: 2. Криптография и теория
Contents: Содержание
В теоретической криптографии существуют два основных
подхода к определению стойкости криптосистем и
криптографических протоколов (в дальнейшем мы будем также
использовать общий термин - криптографические
схемы):
теоретико-информационный и
теоретико-сложностной.
Теоретико-информационный подход предполагает, что
противник, атакующий криптографическую схему, не имеет даже
теоретической возможности получить информацию, достаточную
для осуществления своих целей. Классическим примером здесь
может служить шифр Вернама с одноразовыми ключами,
абсолютно стойкий против пассивного противника.
Подавляющее большинство используемых на практике
криптографических схем не обладает столь высокой
стойкостью. Более того, обычно бывает несложно указать
алгоритм, который выполняет стоящую перед противником
задачу, но не практически, а в принципе. Рассмотрим следующий пример.
Пример 1. (Криптосистема с открытым ключом)
Криптосистема с
открытым ключом полностью
определяется тремя алгоритмами: генерации ключей, шифрования и
дешифрования. Алгоритм генерации ключей 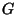 общедоступен; всякий желающий может подать ему на вход
случайную строку
общедоступен; всякий желающий может подать ему на вход
случайную строку  надлежащей длины и получить пару
ключей надлежащей длины и получить пару
ключей  . Открытый ключ . Открытый ключ 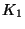 публикуется, а
секретный ключ публикуется, а
секретный ключ 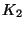 и случайная строка и случайная строка  хранятся в
секрете. Алгоритмы шифрования хранятся в
секрете. Алгоритмы шифрования  и дешифрования и дешифрования
 таковы, что если таковы, что если  - пара ключей,
сгенерированная алгоритмом - пара ключей,
сгенерированная алгоритмом 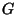 , то , то
 для любого
открытого текста для любого
открытого текста  . Для простоты изложения предполагаем, что открытый
текст и криптограмма имеют одинаковую длину . Для простоты изложения предполагаем, что открытый
текст и криптограмма имеют одинаковую длину  . Кроме того, считаем, что
открытый текст, криптограмма и оба ключа являются
строками в двоичном алфавите. . Кроме того, считаем, что
открытый текст, криптограмма и оба ключа являются
строками в двоичном алфавите.
Предположим теперь, что противник атакует эту
криптосистему. Ему известен открытый ключ 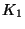 , но
неизвестен соответствующий секретный ключ , но
неизвестен соответствующий секретный ключ 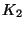 . Противник
перехватил криптограмму . Противник
перехватил криптограмму 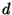 и пытается найти сообщение и пытается найти сообщение  ,
где ,
где  .
Поскольку алгоритм шифрования общеизвестен, противник может просто
последовательно перебрать все возможные сообщения длины .
Поскольку алгоритм шифрования общеизвестен, противник может просто
последовательно перебрать все возможные сообщения длины  , вычислить для
каждого такого сообщения , вычислить для
каждого такого сообщения  криптограмму криптограмму
 и сравнить и сравнить
 с с 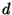 . То сообщение, для которого . То сообщение, для которого  , и будет искомым открытым
текстом. Если повезет, то открытый текст будет найден достаточно быстро. В
худшем же случае перебор будет выполнен за время порядка , и будет искомым открытым
текстом. Если повезет, то открытый текст будет найден достаточно быстро. В
худшем же случае перебор будет выполнен за время порядка
 , где , где  - время, требуемое для
вычисления функции - время, требуемое для
вычисления функции  от сообщений длины от сообщений длины  . Если
сообщения имеют длину порядка 1000 битов, то
такой перебор неосуществим на
практике ни на каких самых мощных компьютерах. . Если
сообщения имеют длину порядка 1000 битов, то
такой перебор неосуществим на
практике ни на каких самых мощных компьютерах.
Мы рассмотрели лишь один из
возможных способов атаки на криптосистему и простейший
алгоритм поиска открытого текста, называемый обычно
алгоритмом полного перебора. Используется также и другое
название: ``метод грубой силы''.
Другой простейший алгоритм поиска открытого текста - угадывание.
Этот очевидный алгоритм требует небольших вычислений, но срабатывает
с пренебрежимо малой вероятностью (при больших длинах текстов).
На самом деле
противник может пытаться атаковать криптосистему различными
способами и использовать различные, более изощренные
алгоритмы поиска открытого текста. Естественно считать
криптосистему стойкой, если любой такой алгоритм требует
практически неосуществимого объема вычислений или срабатывает с пренебрежимо
малой вероятностью.
(При этом противник может использовать не только
детерминированные, но и вероятностные алгоритмы.)
Это и есть теоретико-сложностной подход к определению стойкости.
Для его реализации в отношении того или иного типа криптографических схем
необходимо выполнить следующее:
1) дать формальное определение схемы данного типа;
2) дать формальное определение стойкости схемы;
3) доказать стойкость конкретной конструкции схемы данного
типа.
Здесь сразу же возникает ряд проблем.
Во-первых, в криптографических схемах, разумеется, всегда используются
фиксированные значения параметров. Например,
криптосистемы разрабатываются для ключей длины, скажем, в
256 или 512 байтов. Для применения же
теоретико-сложностного подхода необходимо, чтобы задача,
вычислительную сложность которой предполагается
использовать, была массовой. Поэтому в теоретической
криптографии рассматриваются математические модели
криптографических схем. Эти модели зависят от некоторого
параметра, называемого параметром безопасности, который
может принимать сколь угодно большие значения (обычно для
простоты предполагается, что параметр безопасности может
пробегать весь натуральный ряд).
Во-вторых, определение стойкости криптографической схемы
зависит от той задачи, которая стоит перед противником, и
от того, какая информация о схеме ему доступна. Поэтому
стойкость схем приходится определять и исследовать отдельно
для каждого предположения о противнике.
В-третьих, необходимо уточнить, какой объем вычислений
можно считать ``практически неосуществимым''. Из сказанного
выше следует, что эта величина не может быть просто
константой, она должна быть представлена функцией от
растущего параметра безопасности. В соответствии с тезисом
Эдмондса алгоритм считается эффективным, если время его
выполнения ограничено некоторым полиномом от длины входного
слова (в нашем случае - от параметра безопасности). В
противном случае говорят, что вычисления по данному
алгоритму практически неосуществимы. Заметим также, что
сами криптографические
схемы должны быть эффективными,
т.е. все вычисления, предписанные той или иной схемой,
должны выполняться за полиномиальное время.
В-четвертых, необходимо определить, какую вероятность можно
считать пренебрежимо малой. В
криптографии принято считать
таковой любую вероятность, которая для любого полинома
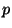 и для всех достаточно больших и для всех достаточно больших  не превосходит не превосходит
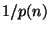 , где , где  - параметр безопасности. - параметр безопасности.
Итак, при наличии всех указанных выше определений, проблема
обоснования стойкости криптографической схемы свелась к
доказательству отсутствия полиномиального алгоритма,
который решает задачу, стоящую перед противником.
Но здесь возникает еще одно и весьма серьезное препятствие:
современное состояние теории сложности вычислений не
позволяет доказывать сверхполиномиальные
нижние оценки сложности для конкретных задач
рассматриваемого класса. Из этого следует, что на данный
момент стойкость криптографических схем может быть
установлена лишь с привлечением каких-либо недоказанных
предположений. Поэтому основное направление исследований
состоит в поиске
наиболее слабых достаточных условий (в
идеале - необходимых и достаточных) для существования
стойких схем каждого из типов.
В основном, рассматриваются
предположения двух типов - общие (или
теоретико-сложностные) и теоретико-числовые, т.е. предположения о сложности конкретных теоретико-числовых
задач. Все эти предположения в литературе обычно называются
криптографическими.
Ниже мы кратко рассмотрим несколько интересных
математических объектов, возникших на стыке теории
сложности и криптографии.
Более подробный обзор по этим вопросам можно найти в
книге [1].
Next: 2.2. Криптография и гипотеза
Up: 2. Криптография и теория
Previous: 2. Криптография и теория
Contents: Содержание
|

