Next: ...к задачам пятой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам третьей олимпиады
Contents: Содержание
4.1. Исходный текст состоит из 48 букв, следовательно, при
зашифровании было использовано три положения решетки полностью и еще
три буквы вписаны в четвертом положении. Значит, незаполненные 12
клеток совпадают с вырезами решетки в четвертом положении. Так как
текст вписывается последовательно, то неизвестные нам три выреза могут
располагаться только в первой строке таблицы и первых пяти клетках
второй строки (до первого известного выреза). Считаем, что трафарет
лежит в четвертом положении. Учитывая, что в одну клетку листа
нельзя вписать две буквы, получаем, что вырезы могут быть только в
отмеченных знаком ``?'' местах трафарета
(`` '' - места известных вырезов): '' - места известных вырезов):
Очевидно, что из отмеченных в первой строке двух клеток
вырезается только одна (так как они совмещаются поворотом). Получаем
два возможных варианта решетки (либо первый ``?'', либо второй
``?'' в первой строке). Читаемый текст
получается при
втором варианте.
Ответ: ПОЛЬЗУЯСЬШИФРОМРЕШЕТКАНЕЛЬЗЯОСТАВЛЯТЬПУСТЫЕМЕСТА
4.2. Один из вариантов решения состоит из следующих этапов.
1. 19=н из второй строки (``19,2 19,5'').
2. 29=о из третьей строки (``29,н,10'') и 10=а или 10=и.
3. 14=щ из ``но,14,но''.
4. 8=д, 2=е, 10=и из ``денно и нощно''.
Получили текст:
5. 5=а и 27=з из второй строки.
6. 17=в 6=п 16=й - последнее слово второй строки - водопой.
Получили текст:
7. 21=т 18=у 28=л 20=с из последней строки ``ищут веселой толпой''.
8. 11=р из ``зве11ей'' первой строки.
Итак,
9. 24=г из ``егерей''.
10. 12=б 3=ю из ``бегают''.
11. 31=ы 22=ч из ``добычей''.
Ответ: Бегают по лесу стаи зверей -
Не за добычей, не на водопой:
Денно и нощно они егерей
Ищут веселой толпой.
4.3. Ответ:
 . .
4.4. Занумеруем буквы латинского алфавита последовательно
числами от 1 до 24. Пусть 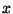 - некоторое число от 1 до 24, а - некоторое число от 1 до 24, а
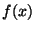 - число, в которое переходит - число, в которое переходит 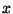 на втором этапе. Тогда
перестановочность этапов можно записать в следующем виде: на втором этапе. Тогда
перестановочность этапов можно записать в следующем виде:

Это означает, что соседние числа 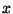 и и  на втором этапе переходят
в соседние же числа на втором этапе переходят
в соседние же числа 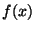 и и  , т.е. второй этап - тоже
сдвиг. Последовательное применение двух сдвигов - очевидно тоже
сдвиг и остается рассмотреть 24 варианта различных сдвигов.
Читаемый текст определяется однозначно. Осложнения, связанные с
переходом Z в A, устраняются либо переходом к остаткам при
делении на 24, либо выписыванием после буквы Z второй раз алфавита
AB...Z. , т.е. второй этап - тоже
сдвиг. Последовательное применение двух сдвигов - очевидно тоже
сдвиг и остается рассмотреть 24 варианта различных сдвигов.
Читаемый текст определяется однозначно. Осложнения, связанные с
переходом Z в A, устраняются либо переходом к остаткам при
делении на 24, либо выписыванием после буквы Z второй раз алфавита
AB...Z.
Ответ:
INTER ARMA SILENT MUSAE
( интер интер  арма си арма си лент му лент му зэ - когда гремит оружие, музы молчат). зэ - когда гремит оружие, музы молчат).
4.5. Составим возможные варианты переданных букв:
Выбирая вторую и последнюю
группу букв (где есть короткие колонки букв),
определяем слова, им
соответствующие: ВЯЗ, ЭТАЖ. В
исходных словах 33 буквы, поэтому буквы В, Я, З, Э, Т, А, Ж
уже использованы и их можно вычеркнуть из всех колонок:
Из нескольких вариантов, например, в третьей группе:
выбираем варианты так, чтобы каждая буква использовалась один раз. Продолжая
таким образом, получим ответ.
Ответ:БЫК
ВЯЗ
ГНОЙ
ДИЧЬ
ПЛЮЩ
СЪ М
ЦЕХ
ШУРФ
ЭТАЖ М
ЦЕХ
ШУРФ
ЭТАЖ
4.6. Заметим, что
 для всех
натуральных для всех
натуральных  . Складывая почленно эти равенства при . Складывая почленно эти равенства при
 ,
получим ,
получим
 . По условию . По условию  . Следовательно,
справедливо соотношение . Следовательно,
справедливо соотношение  . .
Ясно, что при расшифровании так же, как и при зашифровании,
вместо чисел  , ,  , ,  , ,  , ,  , ,
 , ,  можно воспользоваться их остатками от деления
на 30. Так как для каждого целого неотрицательного можно воспользоваться их остатками от деления
на 30. Так как для каждого целого неотрицательного 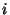

где  - некоторое целое число, то получаем следующие остатки при
делении чисел - некоторое целое число, то получаем следующие остатки при
делении чисел
 на 30: на 30:
Заключительный этап представлен в таблице:
|
шифрованное сообщение |
К |
Е |
Н |
З |
Э |
Р |
Е |
|
числовое шифрованноесообщение |
9 |
5 |
12 |
7 |
27 |
15 |
5 |
|
шифрующий отрезок |
0 |
3 |
12 |
3 |
12 |
15 |
18 |
|
числовое исходное сообщение |
9 |
2 |
0 |
4 |
15 |
0 |
17 |
|
исходное сообщение |
К |
В |
А |
Д |
Р |
А |
Т |
|
4.7. Ответ:
 ; ;
 . .
Next: ...к задачам пятой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам третьей олимпиады
Contents: Содержание
|

