8.3.2 Схема Якоби

Автономная система электронных платежей, предложенная Якоби в работе [Yac1], интересна тем, что в ее конструкции задействованы как широко используемые на практике схемы электронной подписи RSA и Эль Гамаля, так и последние достижения теории -- доказательства с нулевым разглашением. При этом доказательства с нулевым разглашением используются только в тех транзакциях, которые будут выполняться достаточно редко, что обеспечивает высокую эффективность системы.

В системе имеются четыре участника: центр сертификации (ЦС), банк, покупатель и продавец, и шесть транзакций: выдача начального сертификата, обновление сертификата, снятие со счета, платеж, депозит и обмен монет.

Банк и ЦС используют схему электронной подписи RSA, а клиенты -- схему Эль Гамаля. Пусть , , и , ,  -- соответственно открытая и секретная экспоненты и модуль банка и ЦС. Пусть  -- целое число, и обозначает строку из нулей.

Через обозначается модуль схемы Эль Гамаля (который, вообще говоря, может быть различным для различных клиентов). Пусть , и  -- общедоступная хэш-функция с трудно обнаружимыми коллизиями (в работе -- collision free one way hash function; представляется, что в качестве можно использовать одностороннюю перестановку). Иногда требуется такая же функция для ; она обозначается той же буквой.

Секретный ключ клиента представляет собой конкатенацию его имени и случайной строки , а его открытый ключ есть , где  -- общедоступный порождающий для .

Выдача начального сертификата. Клиент выбирает , вычисляет и посылает ЦС и . Затем клиент доказывает ЦС с нулевым разглашением, что содержит . Поскольку соответствующий предикат принадлежит NP, существование такого доказательства гарантируется известной теоремой Гольдрайха, Микали и Вигдерсона [GMW2]. Это же замечание справедливо и для протоколов доказательства в следующих двух транзакциях.

Если ЦС принимает доказательство, он подписывает , т. е. вычисляет и посылает это значение клиенту , который вычисляет сертификат .

Обновление сертификата. Клиент посылает ЦС сертификат , заготовку , где -- новое значение открытого ключа, и доказывает с нулевым разглашением, что соответствующие секретные ключи (старый и новый) содержат одно и то же имя .

Если ЦС принимает доказательство, то он вычисляет и посылает это значение клиенту, который вычисляет новый сертификат .

Снятие со счета. Клиент выбирает наудачу число , вычисляет , , посылает банку и доказывает с нулевым разглашением, что построено правильно. В частности, клиент должен доказать, что секретный ключ, соответствующий , содержит его имя .

Если банк принимает доказательство, он вычисляет и посылает это значение клиенту , который вычисляет . Тройка является электронной монетой.

Платеж. Покупатель посылает продавцу монету . Продавец проверяет подпись банка и, если она корректна, требует от покупателя подписать выбранное наудачу значение , используя и 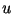, входящие в состав монеты. Т. е., он требует подпись , которую проверяет, используя открытый ключ .

Депозит. Продавец передает банку полученную от покупателя электронную монету, запрос и подпись . Банк проверяет по специальному регистру, не была эта монета потрачена ранее. Если будет обнаружено такое нарушение, то у банка будут две различные подписи, вычисленные с помощью одной и той же пары для двух различных запросов . По известному свойству подписи Эль Гамаля, этой информации достаточно, чтобы вычислить , а значит, и . Поскольку секретный ключ содержит имя , нарушитель будет идентифицирован.

Если никаких нарушений не обнаружено, банк заносит полученную монету в регистр и кладет соответствующую сумму на счет продавца.

Обмен монет. Клиент обращается в банк анонимно, посылает старые монеты и просит обменять их на новые монеты на ту же сумму. Банк проверяет полученные монеты по регистру и если какая-либо монета была потрачена дважды, идентифицирует нарушителя таким же образом, как это делается в транзакции депозита. Если никаких нарушений не обнаружено, клиент предъявляет сертификат и для каждой запрашиваемой монеты высылает значение . Банк проверяет сертификат и, если сертификат подлинный, подписывает монеты и передает их клиенту. Поскольку здесь не использовался затемняющий множитель, банк всегда узнает эти монеты в дальнейшем, но он не имеет никакой информации о том, кому из клиентов они были выданы.

Схема может быть очевидным образом обобщена на случай, когда в обращении находятся монеты различного номинала. В таком случае, каждому номиналу соответствует своя секретная экспонента .

Чтобы избежать неограниченного возрастания длины регистра, в который банк заносит все полученные монеты, предлагается ввести для монет срок действия, по истечении которого они не принимаются ни в какие платежи. Транзакция обмена монет позволяет каждому клиенту анонимно обменивать выходящие из обращения монеты на новые.

Главный недостаток данной схемы заключается в крайней неэффективности транзакции снятия со счета. Однако, автор относит эту транзакцию к числу редко используемых. Другими словами, схема может быть эффективна в том случае, если клиенты редко обращаются в банк, чтобы снять деньги со счета, а, в основном, расплачиваются электронными монетами друг с другом и периодически меняют в банке старые монеты на новые.