




Вперед: 8.3.4 Переводимая электронная монета
Вверх: 8.3 Электронная монета
Назад: 8.3.2 Схема Якоби
Содержание
Предметный указатель
Схема Брандса [Brand] выделяется из всех автономных
систем электронных платежей благодаря, во-первых, своей
высокой эффективности, а во-вторых, попыткой обосновать ее
стойкость. В работе [Brand] сформулирован ряд
результатов, утверждающих стойкость этой системы. Мы
оцениваем их осторожно, как попытку обоснования стойкости,
поскольку в работе нет достаточно формальных определений, а
за доказательствами автор отсылает к своему техническому
отчету.
Всюду ниже мы будем обозначать покупателя через U, а
продавца -- через S.
Инициализация системы. Банк выбирает тройку
порождающих
 группы группы  простого порядка и
число простого порядка и
число
 . Кроме того, он выбирает две хэш-функции
(в работе они названы хэш-функциями с трудно обнаружимыми
коллизиями) . Кроме того, он выбирает две хэш-функции
(в работе они названы хэш-функциями с трудно обнаружимыми
коллизиями)  и и  . .  отображает пятерки элементов
группы отображает пятерки элементов
группы  в в
 , а , а  -- пары элементов -- пары элементов  -- в
-- в
 . Кроме того, . Кроме того,  зависит, например, от
некоторого значения зависит, например, от
некоторого значения  , идентифицирующего S, а также --
от времени и даты , идентифицирующего S, а также --
от времени и даты 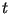 выполнения транзакции. Отмечается,
что этот формат функции выполнения транзакции. Отмечается,
что этот формат функции  выбран лишь для примера. Банк
публикует описание группы выбран лишь для примера. Банк
публикует описание группы  (простые числа (простые числа  и и  ,
если ,
если
 ), тройку ), тройку
 и функции и функции
 , ,  в качестве своего открытого ключа. Секретным
ключом банка является число в качестве своего открытого ключа. Секретным
ключом банка является число  . В описаниях протоколов
появляется также еще некоторое значение . В описаниях протоколов
появляется также еще некоторое значение  , которое в
работе нигде не определяется, но из анализа протоколов можно
понять, что , которое в
работе нигде не определяется, но из анализа протоколов можно
понять, что  и это значение должно публиковаться как
часть открытого ключа. и это значение должно публиковаться как
часть открытого ключа.
Подпись
 банка для пары банка для пары  , ,
 есть четверка
есть четверка  , где , где
 , ,
 ,
такая, что ,
такая, что

Открытие счета. U выбирает число
 и
вычисляет и
вычисляет
 . Если . Если  , то U передает
значение , то U передает
значение  банку, а банку, а  хранит в секрете. Для
безопасности банка существенно, чтобы значения хранит в секрете. Для
безопасности банка существенно, чтобы значения  были
различными для разных клиентов. Банк вычисляет были
различными для разных клиентов. Банк вычисляет
 и передает это значение U.
и передает это значение U.
Снятие со счета. Прежде чем снять электронную
монету со счета, U должен пройти аутентификацию, т. е. доказать банку, что он является владельцем данного счета.
Затем выполняется следующий протокол.
1.
Банк выбирает число
 и посылает и посылает  и и
 клиенту U. клиенту U.
2.
U выбирает три числа
 , ,
 и
вычисляет и
вычисляет
 , ,
 и и  .
Кроме того, U выбирает числа .
Кроме того, U выбирает числа
 и вычисляет и вычисляет
 и и
 . Затем он вычисляет . Затем он вычисляет
 и посылает запрос и посылает запрос
 банку.
банку.
3.
Банк посылает ответ
 и снимает
со счета U соответствующую сумму.
U принимает ответ тогда и только тогда, когда и снимает
со счета U соответствующую сумму.
U принимает ответ тогда и только тогда, когда  и и
 . Если эти условия выполнены, U вычисляет . Если эти условия выполнены, U вычисляет
 . Пара . Пара  и подпись банка и подпись банка
 для нее образуют электронную монету. для нее образуют электронную монету.
Платеж. В транзакции платежа U и S выполняют следующий
протокол.
1.
U посылает S электронную монету:  , ,  , ,
 . .
2.
Если  , то S вычисляет запрос , то S вычисляет запрос
 , где , где  -- идентификатор S, а -- идентификатор S, а 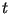 --
дата и время транзакции. S посылает U значение --
дата и время транзакции. S посылает U значение  . .
3.
U вычисляет ответы
 и и
 и посылает их S.
S принимает монету тогда и только тогда, когда и посылает их S.
S принимает монету тогда и только тогда, когда
 является подписью для
является подписью для  и и
 . .
Депозит. S посылает банку
 , а также дату и время транзакции
платежа , а также дату и время транзакции
платежа 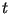 . Если . Если  , то банк не принимает монету. В
противном случае он вычисляет , то банк не принимает монету. В
противном случае он вычисляет  , используя полученные
данные и идентификатор , используя полученные
данные и идентификатор  продавца S. Затем банк
проверяет, что продавца S. Затем банк
проверяет, что
 и что и что
 является подписью для
является подписью для  . Если все корректно, то банк
проверяет, не была ли монета потрачена ранее. Если нет, то
банк запоминает . Если все корректно, то банк
проверяет, не была ли монета потрачена ранее. Если нет, то
банк запоминает
 и кладет монету на счет S. и кладет монету на счет S.
Если данная электронная монета уже была потрачена ранее, то
банк имеет в своем распоряжении две несовпадающие тройки
 и и
 и может вычислить
идентификатор нарушителя и может вычислить
идентификатор нарушителя
 . .
Из утверждений, сформулированных в работе [Brand],
вытекает, в предположении трудности задачи дискретного
логарифмирования и стойкости протокола аутентификации
Шнорра, безопасность вышеприведенных протоколов для всех
участников. Это означает, что:
клиенты не могут создавать электронные монеты без участия
банка;
если продавец действует в транзакции платежа согласно
протоколу, то покупатель не может обмануть его, заплатив
фальшивой монетой;
если покупатель действует согласно протоколам, то банк не
может ложно обвинить его, предоставив в арбитраж
сфабрикованное доказательство повторной траты одной и той
же электронной монеты;
сообщения, посылаемые в ходе выполнения протоколов, не
требуют шифрования, т. е. противник, подслушивающий
транзакции снятия со счета, не может сам создать
электронную монету, а подслушивание транзакции платежа не
помогает выполнить депозит перехваченной монеты на другой
счет.
Кроме того, при некотором предположении, которое
представляется более сильным, чем предположение о трудности
задачи Диффи -- Хеллмана, доказывается, что нарушитель,
дважды потративший одну электронную монету, всегда будет
идентифицирован.
Поскольку, как уже отмечалось выше, все эти результаты
сформулированы недостаточно строго, мы не воспроизводим их
здесь.





Вперед: 8.3.4 Переводимая электронная монета
Вверх: 8.3 Электронная монета
Назад: 8.3.2 Схема Якоби
Содержание
Предметный указатель
|

