




Вперед: 9. Интеллектуальные карточки в банковских системах
Вверх: 8. Банковские криптографические протоколы
Назад: 8.3.4 Переводимая электронная монета
Содержание
Предметный указатель
8.4 Электронные бумажники
Электронным бумажником, вообще говоря, может считаться
любое транспортируемое индивидуальное платежное средство,
предназначенное для расчетов в системах электронных
платежей. В некоторых работах, посвященных банковским
криптографическим протоколам, авторы пишут, что в будущем
бумажные деньги будут заменены электронными бумажниками,
т. е. интеллектуальными карточками, "набитыми" электронными деньгами. Отметим, все же, что не все подобные
платежные средства обладают следующим свойством обычного
бумажника: бумажник не несет в себе никакой информации о
владельце и может быть передан любому другому лицу "на
законных основаниях".
В автономных системах электронных платежей термин
"электронный бумажник" употребляется обычно для
обозначения устройства, предназначенного для предотвращения
злоупотреблений со стороны клиентов (т. е. повторной траты
одной и той же электронной монеты). Электронные бумажники
были предложены Шаумом [BCCFP] как устройства,
состоящие из микрокомпьютера, который контролирует клиент и
которому он доверяет, и защищенного устройства, называемого
наблюдателем. Назначение наблюдателя состоит в контроле за
всеми платежами, которые производит клиент. Поскольку
платеж без содействия наблюдателя невозможен, это
обеспечивает в автономных системах электронных платежей
такую же безопасность банка, как в централизованных
системах. Однако, при этом требуется, чтобы содержимое
наблюдателя было недоступно клиенту. Таким образом, в
данной модели безопасность банка основывается не только на
математических, но и на физических предположениях. Отметим
все же, что эти предположения весьма слабые: достаточно,
чтобы задача доступа к содержимому наблюдателя не была
слишком простой. Ведь во всех автономных системах
электронных платежей, основанных на использовании
бумажников, сохраняется контроль повторной траты, который
осуществляется во время выполнения транзакции депозита (на
случай, если будет "взломана" защита наблюдателя). С
другой стороны, безопасность клиента обеспечивается тем,
что наблюдатель не общается с внешним миром
непосредственно, а только через компьютер клиента.
Ниже мы приводим описание схемы электронной подписи для
бумажников с наблюдателями [CrP] и автономной системы
электронных платежей из работы Брандса [Brand].
В работе [CrP] рассматривается задача создания схемы
электронной подписи, в которой клиент подписывает сообщения
совместно с наблюдателем и только такие подписи считаются
действительными, но при этом должна обеспечиваться
безусловная неотслеживаемость действий клиента, даже если
содержимое наблюдателя станет известно противнику.
Для того чтобы отличать подлинных наблюдателей от
поддельных, центр выдачи наблюдателей (таким центром может
быть банк) снабжает выдаваемые наблюдатели схемой
электронной подписи, называемой изначальной схемой. Однако,
эту схему нельзя использовать непосредственно, т. к. она
идентифицирует наблюдателя, а следовательно, и клиента.
Вместо этого, изначальная схема подписи используется для
получения так называемого валидатора в
центре выдачи валидаторов (VIC). Валидатор состоит из секретного ключа,
соответствующего ему открытого ключа и подписи VIC для
открытого ключа. При этом VIC не получает никакой
информации о том, какой именно валидатор он выдал, поэтому
клиент может использовать валидатор для подписания
сообщений, не опасаясь быть отслеженным.
В работе [CrP] сформулированы следующие требования к
протоколу выдачи валидаторов (A обозначает компьютер
клиента, а OA -- его наблюдателя):
1.
Клиент не может получить валидатор, для которого он
знает секретный ключ.
2.
В процессе выполнения протокола наблюдатель и VIC не
могут передать друг другу никакой информации (даже при
неограниченных вычислительных возможностях).
3.
Идентификатор наблюдателя может быть известен VIC.
4.
VIC не получает никакой информации о выданном им
валидаторе.
5.
Открытый ключ валидатора (и подпись для него)
известны только A; VIC и OA не получают о них никакой
информации.
6.
OA и A каждый получают лишь часть секретного ключа,
так что подписывать сообщения они могут только совместно
(это -- своего рода схема разделения секрета).
Схема подписи, основанная на валидаторах, должна
удовлетворять следующим требованиям (получатель подписи
называется проверяющим):
1.
A и OA совместно могут подписать любое сообщение.
2.
Если A следует протоколу, то OA, VIC и проверяющий
совместно не могут вычислить секретный ключ A.
3.
Если OA и VIC оба следуют протоколу выдачи
валидатора, то A не может самостоятельно подписать
сообщение, которое не желает подписывать наблюдатель.
4.
Протокол проверки подписи должен быть интерактивным.
5.
Никакой противник, даже обладающий неограниченными
вычислительными возможностями, не может установить
соответствие между выполнениями протокола подписи и
протокола выдачи валидатора.
Ниже приводятся протокол выдачи валидаторов и основанная на
валидаторах схема подписи, предложенные в работах
[BCCFP] и [CP92], и цитируемые по статье
[CrP].
Пусть  и и  -- простые числа, причем -- простые числа, причем  делит делит 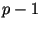 и и
 -- элемент порядка -- элемент порядка  . Тогда . Тогда  --
группа, порождаемая --
группа, порождаемая  . Пусть . Пусть  -- другой порождающий
группы -- другой порождающий
группы  такой, что A не знает дискретный логарифм такой, что A не знает дискретный логарифм  по основанию
по основанию  . Открытый ключ VIC есть . Открытый ключ VIC есть  , где , где
 -- его секретный ключ. Кроме того, предполагается, что
всем участникам протоколов известна некоторая
криптографическая (в работе она названа односторонней --
one-way) хэш-функция -- его секретный ключ. Кроме того, предполагается, что
всем участникам протоколов известна некоторая
криптографическая (в работе она названа односторонней --
one-way) хэш-функция  , отображающая входы произвольной
длины в , отображающая входы произвольной
длины в
 . .
Протоколы основаны на предположении о трудности
сертифицированной задачи дискретного логарифмирования,
т. е. задачи вычисления дискретных логарифмов при
известной факторизации 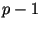 . .
Замечание 2.
В работе [CrP] в описаниях протоколов авторы опускают
модули, по которым приводятся вычисляемые величины, и в
некоторых случаях, не указывают, из каких множеств
выбираются случайные величины. Мы цитируем протоколы в
соответствии с оригиналом. Недостающие подробности, как
правило, легко восстанавливаются по контексту.
Протокол выдачи валидатора
1.
A выбирает
 , вычисляет , вычисляет  и
посылает это значение OA ( и
посылает это значение OA ( -- часть секретного ключа,
известная A, а -- часть секретного ключа,
известная A, а  -- затемняющий множитель). -- затемняющий множитель).
2.
OA выбирает
 и посылает A значение и посылает A значение  (
( -- секретный ключ). -- секретный ключ).
3.
A вычисляет открытый ключ  , выбирает , выбирает
 , вычисляет затемненный открытый ключ , вычисляет затемненный открытый ключ
 и посылает OA значение
и посылает OA значение  . .
4.
OA вычисляет
 и подпись и подпись
 для для  , вычисленную с помощью изначальной
схемы электронной подписи, и посылает подпись A. , вычисленную с помощью изначальной
схемы электронной подписи, и посылает подпись A.
5.
A проверяет полученную от OA подпись и передает VIC
значение  и подпись и подпись  . .
6.
VIC проверяет подпись, чтобы убедиться, что значение
 было выбрано с участием наблюдателя. Затем выбирает было выбрано с участием наблюдателя. Затем выбирает
 , вычисляет , вычисляет
 и и  . VIC
высылает A значения . VIC
высылает A значения  , ,  и и  . .
7.
A выбирает случайные 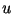 и и  и вычисляет и вычисляет
 и и
 , ,
 и
соответствующий запрос и
соответствующий запрос
 . Затем A вычисляет . Затем A вычисляет
 и посылает это значение VIC. и посылает это значение VIC.
8.
VIC вычисляет
 и посылает это значение
A. и посылает это значение
A.
9.
A вычисляет  и проверяет, что и проверяет, что  и и
 . .
Четверка  является подписью для открытого ключа является подписью для открытого ключа  . .
В описании схемы подписи предполагается, что A
предварительно высылает открытый ключ  и подпись для
него проверяющему. Подписывается сообщение и подпись для
него проверяющему. Подписывается сообщение  . .
Схема подписи
1.
OA выбирает
 , вычисляет , вычисляет  , ,
 , ,  и посылает A значения и посылает A значения  , ,  и и
 . .
2.
A выбирает случайные 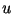 и и  и вычисляет и вычисляет
 , ,
 и и  . Затем A вычисляет . Затем A вычисляет
 , ,  и посылает OA запрос и посылает OA запрос  . .
3.
OA вычисляет ответ
 и посылает его A. и посылает его A.
4.
A проверяет, что
 (значение (значение
 известно после выполнения протокола выдачи
валидатора) и что известно после выполнения протокола выдачи
валидатора) и что
 . Далее A вычисляет . Далее A вычисляет
 и посылает проверяющему пятерку и посылает проверяющему пятерку
 . .
5.
Проверяющий вычисляет
 и проверяет,
что и проверяет,
что  и и  . .
Для обеспечения интерактивности проверяющего (требование 4)
предлагается предоставить ему возможность выбирать
дополнительный случайный параметр, используемый при
вычислении хэш-функции  . .
В работе [CrP] даны наброски доказательств стойкости
этих протоколов. Поскольку определения и формулировки в
этих тезисах недостаточно строгие, мы не приводим их в
данном обзоре.
Фергюсон [Ferg] предложил автономную систему
электронных платежей, основанную на использовании
бумажников, которая базируется на тех же принципах, что и
данная схема подписи. Мы, однако, приведем систему
электронных платежей, разработанную Брандсом [Brand],
поскольку, во-первых, она является модификацией системы,
рассмотренной в предыдущем подразделе, а во-вторых, в
работе [Brand] сформулированы некоторые результаты о
ее стойкости.
Инициализация системы. Такая же, как в исходной
системе электронных платежей Брандса.
Открытие счета. U выбирает число
 и
вычисляет и
вычисляет
 . U передает значение . U передает значение  банку, а банку, а
 хранит в секрете. Для безопасности банка существенно,
чтобы значения хранит в секрете. Для безопасности банка существенно,
чтобы значения  были различными для разных клиентов. были различными для разных клиентов.
Затем банк выдает U наблюдателя O, у которого в памяти
хранится число  , выбранное случайным образом из , выбранное случайным образом из
 и недоступное U. Пусть и недоступное U. Пусть
 .
Банк вычисляет .
Банк вычисляет
 и и
 и
передает U значения и
передает U значения
 и и  . .
Снятие со счета. Прежде чем снять электронную
монету со счета, U должен пройти аутентификацию, т. е. доказать банку, что он является владельцем данного счета.
Затем выполняется следующий протокол.
1.
O выбирает
 и посылает U значение и посылает U значение
 . Хотя этот шаг описывается как часть
протокола, он может быть выполнен заранее. . Хотя этот шаг описывается как часть
протокола, он может быть выполнен заранее.
2.
Банк выбирает число
 и посылает и посылает  и и
 клиенту U. клиенту U.
3.
U выбирает четыре числа
 , ,
 и вычисляет и вычисляет
 , ,
 и и  .
Кроме того, U выбирает числа .
Кроме того, U выбирает числа
 и вычисляет и вычисляет
 и и
 . Затем он вычисляет . Затем он вычисляет
 и посылает запрос и посылает запрос
 банку.
банку.
4.
Банк посылает ответ
 и снимает
со счета U соответствующую сумму.
U принимает ответ тогда и только тогда, когда и снимает
со счета U соответствующую сумму.
U принимает ответ тогда и только тогда, когда  и и
 . Если эти сравнения выполнены, U вычисляет . Если эти сравнения выполнены, U вычисляет
 . Пара . Пара  и подпись банка и подпись банка
 для нее образуют электронную монету. для нее образуют электронную монету.
Платеж. В транзакции платежа U и S выполняют следующий
протокол.
1.
U посылает S электронную монету:
 . .
2.
Если  , то S вычисляет запрос , то S вычисляет запрос
 , где , где  -- идентификатор S, а -- идентификатор S, а 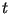 --
дата и время транзакции. S посылает U значение --
дата и время транзакции. S посылает U значение  . .
3.
U вычисляет
 и посылает это
значение наблюдателю O. и посылает это
значение наблюдателю O.
4.
Если значение  находится в памяти наблюдателя,
то O вычисляет ответ находится в памяти наблюдателя,
то O вычисляет ответ
 , стирает , стирает
 и посылает ответ U. В противном случае наблюдатель
блокирует выполнение транзакции платежа. и посылает ответ U. В противном случае наблюдатель
блокирует выполнение транзакции платежа.
5.
U проверяет, что
 . Если равенство выполняется, вычисляет ответы . Если равенство выполняется, вычисляет ответы
 и и
 и
посылает их S.
S принимает монету тогда и только тогда, когда и
посылает их S.
S принимает монету тогда и только тогда, когда
 является подписью для
является подписью для  и и
 . .
Депозит. Эта транзакция ничем не отличается от
транзакции депозита в исходной системе электронных платежей
Брандса.
В работе [Brand] сформулированы результаты,
утверждающие безопасность банка и клиентов в данной
системе. Кроме того, утверждается, что если защита
наблюдателя "взломана", то безопасность банка такая же,
как в исходной системе.





Вперед: 9. Интеллектуальные карточки в банковских системах
Вверх: 8. Банковские криптографические протоколы
Назад: 8.3.4 Переводимая электронная монета
Содержание
Предметный указатель
| 
