




Вперед: 11.4 Логарифмирование в Z_n*
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.4 Алгоритм Хеллмана - Рейнери
Содержание
Предметный указатель
Д. Копперсмит [Copp] предложил для группы
 алгоритм логарифмирования с эвристической
оценкой сложности алгоритм логарифмирования с эвристической
оценкой сложности
 где где  --
константа
Дальнейшее обсуждение деталей этого алгоритма и его
реализации на ЭВМ проведено в [Odl] (см. также
[McC90]). Алгоритм основан на нахождении удобного
представления --
константа
Дальнейшее обсуждение деталей этого алгоритма и его
реализации на ЭВМ проведено в [Odl] (см. также
[McC90]). Алгоритм основан на нахождении удобного
представления
![$ GF(2^n)=GF(2)[y]/(f(y))$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1386.gif) , где , где
 -- неприводимый многочлен, причем -- неприводимый многочлен, причем  -- многочлен небольшой степени (меньше
-- многочлен небольшой степени (меньше  ).
Например, для ).
Например, для  можно взять можно взять  . Схема
алгоритма заключается в следующем:
1.
На первом этапе мы ищем логарифмы тех элементов . Схема
алгоритма заключается в следующем:
1.
На первом этапе мы ищем логарифмы тех элементов
 , которые представимы многочленами из , которые представимы многочленами из ![$ GF(2)[y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1392.gif) небольшой степени. Выбираем параметры
небольшой степени. Выбираем параметры  , ,  , ,  .
Затем, перебирая многочлены .
Затем, перебирая многочлены
![$ u,v\in GF(2)[y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1394.gif) степени не
выше степени не
выше  , полагаем , полагаем  и вычисляем и вычисляем
 .
Поскольку .
Поскольку  есть степень двойки, то есть степень двойки, то
 . При удачном выборе . При удачном выборе  , ,  , ,  степень многочлена
степень многочлена
 будет невелика; здесь
преимущество метода Копперсмита заключается в том, что и будет невелика; здесь
преимущество метода Копперсмита заключается в том, что и
 и и  имеют не очень большую степень. Мы накапливаем те
пары имеют не очень большую степень. Мы накапливаем те
пары  , ,  , которые раскладываются в произведение
неприводимых многочленов , которые раскладываются в произведение
неприводимых многочленов
![$ s\in GF(2)[y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1399.gif) небольшой степени,
а именно, не превосходящей небольшой степени,
а именно, не превосходящей
 .
Множество всех таких неприводимых многочленов мы обозначим
через .
Множество всех таких неприводимых многочленов мы обозначим
через  . .
Пусть
Тогда имеем соотношение для логарифмов
 Получив много таких соотношений, находим значения
Получив много таких соотношений, находим значения  для
для  . .
2.
На втором этапе для нахождения искомого дискретного
логарифма  мы находим путем случайного перебора
число мы находим путем случайного перебора
число 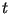 такое, что такое, что
 выражается через
произведение неприводимых многочленов выражается через
произведение неприводимых многочленов  степени не выше степени не выше
 (множество всех таких неприводимых
многочленов мы обозначим через (множество всех таких неприводимых
многочленов мы обозначим через  ): ):
 Далее находим логарифмы элементов
Далее находим логарифмы элементов  с помощью
техники, аналогичной первому этапу. Тогда искомый
дискретный логарифм равен с помощью
техники, аналогичной первому этапу. Тогда искомый
дискретный логарифм равен

Алгоритм Копперсмита позволяет эффективно вычислять
логарифмы в  при при  ; следовательно, эти
поля уже неприменимы для схем криптографии, использующих
высокую сложность логарифмирования (см. [Odl],
[McC90, стр. 69]). При применении суперкомпьютеров
и специальных средств, согласно [McC90, стр. 69],
реально даже логарифмирование в ; следовательно, эти
поля уже неприменимы для схем криптографии, использующих
высокую сложность логарифмирования (см. [Odl],
[McC90, стр. 69]). При применении суперкомпьютеров
и специальных средств, согласно [McC90, стр. 69],
реально даже логарифмирование в  при при  . .





Вперед: 11.4 Логарифмирование в Z_n*
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.4 Алгоритм Хеллмана - Рейнери
Содержание
Предметный указатель
|

