




Вперед: 11.5 Рекомендуемая литература
Вверх: 11. Задача дискретного логарифмирования
Назад: 11.3.5 Алгоритм Копперсмита
Содержание
Предметный указатель
11.4 Логарифмирование в
В работе Райзела [Ries] изучаются
свойства частных Ферма
 где
где  и и  -- взаимно простые целые числа, -- взаимно простые целые числа,
 , а , а  -- функция Кармайкла,
определенная следующим образом. Если -- функция Кармайкла,
определенная следующим образом. Если
 , где , где 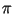 -- конечное множество простых чисел, а
-- конечное множество простых чисел, а
 , то , то
 есть наименьшее общее
кратное чисел есть наименьшее общее
кратное чисел
 при при  ,
которые равны ,
которые равны
 Нетрудно заметить, что
Нетрудно заметить, что
 есть максимум порядков
элементов группы есть максимум порядков
элементов группы
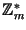 . .
Основным свойством частных Ферма является следующая
формула:
 аналогичная известному свойству логарифмической функции.
Как оказалось, частные Ферма в некоторых случаях могут быть
полезны для вычисления дискретных логарифмов. Так, в
[Ries] показано, что когда
аналогичная известному свойству логарифмической функции.
Как оказалось, частные Ферма в некоторых случаях могут быть
полезны для вычисления дискретных логарифмов. Так, в
[Ries] показано, что когда  является является
 -низким (т. е. если -низким (т. е. если
 , где , где
 -- различные нечетные простые числа, а -- различные нечетные простые числа, а
 , то , то
 , где , где 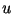 нечетно и не делится ни на одно
из нечетно и не делится ни на одно
из  ), вычисление логарифмов в ), вычисление логарифмов в
 в некоторых
случаях может быть проведено быстро. в некоторых
случаях может быть проведено быстро.
Изучение частных Ферма продолжено в работе Ю. В. Нестеренко
[Нест], где доказано следующее утверждение.
Теорема.
Пусть
 , где , где
 -- различные нечетные
простые числа, а -- различные нечетные
простые числа, а
 , -- , --  -низкое
число, причем -низкое
число, причем
 для любого для любого
 .
Тогда
1)
если .
Тогда
1)
если
 , то
из сравнения , то
из сравнения
 следует, что следует, что
 ; это значит, что ; это значит, что
 по существу
является отображением по существу
является отображением
 ; ;
2)
 ; ;
3)
существует элемент
 порядка порядка  (максимального порядка в группе
(максимального порядка в группе
 ) такой,
что ) такой,
что
 . .
Покажем, как вышеприведенная теорема позволяет эффективно
находить дискретные логарифмы в группе
 по
основанию по
основанию  из п. 3 теоремы. Пусть из п. 3 теоремы. Пусть
 , где , где
 . Тогда согласно основному свойству частных Ферма . Тогда согласно основному свойству частных Ферма
 , откуда можно однозначно
найти искомый дискретный логарифм , откуда можно однозначно
найти искомый дискретный логарифм
 , так как , так как
 . Отметим, что если . Отметим, что если  не
является степенью не
является степенью  в группе в группе
 , то , то
 может принимать совершенно
произвольные значения. может принимать совершенно
произвольные значения.
В той же работе [Нест] указан рекуррентный процесс
построения по данному натуральному  числа числа  ,
удовлетворяющего условиям теоремы и такого, что ,
удовлетворяющего условиям теоремы и такого, что
 и и
 . Однако этот
процесс требует разложения на простые множители некоторых
чисел, что является вычислительно трудной задачей. Кроме
того, в [Нест] с помощью частных Ферма показано, что
если известно разложение . Однако этот
процесс требует разложения на простые множители некоторых
чисел, что является вычислительно трудной задачей. Кроме
того, в [Нест] с помощью частных Ферма показано, что
если известно разложение  на простые множители, то
задача дискретного логарифмирования в группе на простые множители, то
задача дискретного логарифмирования в группе
 сводима за полиномиальное от
сводима за полиномиальное от  время к аналогичным
задачам в группах время к аналогичным
задачам в группах
 , где , где  пробегает множество
простых делителей пробегает множество
простых делителей  . В частности, если . В частности, если  гладкое
(т. е. имеет только небольшие простые делители), то
дискретные логарифмы в группе гладкое
(т. е. имеет только небольшие простые делители), то
дискретные логарифмы в группе
 можно вычислять
эффективно. можно вычислять
эффективно.
В [Kob,
 3, гл. 4, задача 2] предложен простой
способ логарифмирования в циклической группе 3, гл. 4, задача 2] предложен простой
способ логарифмирования в циклической группе
 ;
этот способ сводится к быстрому вычислению логарифма для ;
этот способ сводится к быстрому вычислению логарифма для
 через логарифм для через логарифм для  . .





Вперед: 11.5 Рекомендуемая литература
Вверх: 11. Задача дискретного логарифмирования
Назад: 11.3.5 Алгоритм Копперсмита
Содержание
Предметный указатель
|

