




Вперед: 12.2 Факторизация чисел с экспоненциальной сложностью
Вверх: 12. Задача факторизации больших целых чисел
Назад: 12. Задача факторизации больших целых чисел
Содержание
Предметный указатель
Стойкость наиболее распространенной системы открытого
шифрования RSA и стойкость схемы электронной подписи на
основе RSA определяется сложностью задачи факторизации
больших целых чисел. Поэтому эта задача -- одна из наиболее
важных математических задач современной криптографии. По
популярности она превосходит задачу дискретного
логарифмирования, а также является составной частью
известных алгоритмов дискретного логарифмирования.
Задача факторизации целых чисел -- это задача нахождения по данному
натуральному числу  различных простых чисел различных простых чисел
 и натуральных чисел и натуральных чисел
 таких, что таких, что
 . Отметим, что если
известен некоторый простой делитель . Отметим, что если
известен некоторый простой делитель  числа числа  , то
соответствующее , то
соответствующее  может быть легко найдено
(например, перебором) за полиномиальное от может быть легко найдено
(например, перебором) за полиномиальное от  время.
Поэтому основная трудность задачи факторизации заключается
в нахождении простых делителей время.
Поэтому основная трудность задачи факторизации заключается
в нахождении простых делителей  . .
Все описываемые ниже алгоритмы факторизации сводятся к
нахождению нетривиальных (т. е. положительных и отличных
от 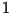 и и  ) делителей числа ) делителей числа  , если , если  составное.
Если мы умеем находить нетривиальные делители, то
разложение составное.
Если мы умеем находить нетривиальные делители, то
разложение  на простые множители может быть получено
следующим образом. Сначала разложим число на простые множители может быть получено
следующим образом. Сначала разложим число  на два
нетривиальных множителя (если на два
нетривиальных множителя (если  составное), затем, в свою
очередь, разложим каждый из этих множителей на два
нетривиальных множителя (если этот исходный множитель
составной), потом то же самое проделаем со всеми составными
множителями, найденными на предыдущем этапе и т. д., пока
все множители не станут простыми. Очевидно, что для
вычисления разложения составное), затем, в свою
очередь, разложим каждый из этих множителей на два
нетривиальных множителя (если этот исходный множитель
составной), потом то же самое проделаем со всеми составными
множителями, найденными на предыдущем этапе и т. д., пока
все множители не станут простыми. Очевидно, что для
вычисления разложения  на простые множители потребуется
находить нетривиальные делители полиномиальное от на простые множители потребуется
находить нетривиальные делители полиномиальное от  число раз.
число раз.
В свою очередь, для нахождения нетривиального делителя  часто используется следующее замечание. Пусть каким-либо
образом найдены целые числа
часто используется следующее замечание. Пусть каким-либо
образом найдены целые числа  такие, что такие, что
 . Тогда если . Тогда если
 для
некоторого для
некоторого
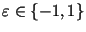 , то , то
 -- искомый нетривиальный делитель -- искомый нетривиальный делитель  . Как обычно,
запись . Как обычно,
запись  здесь и далее обозначает наибольший общий
делитель чисел здесь и далее обозначает наибольший общий
делитель чисел  и и  . .
В настоящее время нет достаточно быстрых алгоритмов для
факторизации целых чисел. Имеющиеся алгоритмы факторизации
по сложности (числу арифметических операций, необходимых
для их реализации) разделяются на три группы (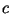 обозначает некоторую константу):
1)
алгоритмы экспоненциальной сложности, делающие
обозначает некоторую константу):
1)
алгоритмы экспоненциальной сложности, делающие
 арифметических операций (см. раздел 12.2); арифметических операций (см. раздел 12.2);
2)
алгоритмы субэкспоненциальной сложности, делающие
 , арифметических операций, где , арифметических операций, где
 (см. раздел 12.3); (см. раздел 12.3);
3)
алгоритм, называемый методом решета числового
поля, и его дальнейшие обобщения, имеющие сложность
 арифметических операций (см. раздел 12.4).
арифметических операций (см. раздел 12.4).
В криптографических схемах, стойкость которых основана
на сложности задачи факторизации целых чисел, в качестве
сложно разлагаемого числа часто выбирают произведение
 двух различных простых чисел. Отметим, что если мы
умеем эффективно вычислять дискретные логарифмы по модулю
такого двух различных простых чисел. Отметим, что если мы
умеем эффективно вычислять дискретные логарифмы по модулю
такого  , то мы можем эффективно разложить , то мы можем эффективно разложить  на простые
множители: на простые
множители:
Теорема 1 [Cha].
Пусть  , где , где  и и  -- различные простые числа.
Предположим, что существует вероятностный полиномиальный
алгоритм, вычисляющий по -- различные простые числа.
Предположим, что существует вероятностный полиномиальный
алгоритм, вычисляющий по
 и и
 некоторый дискретный логарифм
некоторый дискретный логарифм  по основанию по основанию  (т. е. некоторое целое (т. е. некоторое целое  , для которого , для которого
 ) с
вероятностью не менее ) с
вероятностью не менее
 для некоторого полинома для некоторого полинома
 . Тогда существует вероятностный полиномиальный
алгоритм, разлагающий . Тогда существует вероятностный полиномиальный
алгоритм, разлагающий  на простые множители на простые множители  и и  с
вероятностью не менее с
вероятностью не менее  . .
Через
 в теореме 1 обозначена подгруппа,
порожденная элементом в теореме 1 обозначена подгруппа,
порожденная элементом  группы группы
 . .
Таблицы разложений на множители и больших простых чисел
можно найти в [Rie], [BriMS], [GLS],
[Rib]. Самые последние сведения о разложении чисел
вида  , где , где
 , приведены в
[BrRi]. Там собраны все известные (полные и частичные)
разложения этих чисел на множители. , приведены в
[BrRi]. Там собраны все известные (полные и частичные)
разложения этих чисел на множители.





Вперед: 12.2 Факторизация чисел с экспоненциальной сложностью
Вверх: 12. Задача факторизации больших целых чисел
Назад: 12. Задача факторизации больших целых чисел
Содержание
Предметный указатель
|

