Все о геологии :: на главную страницу! Геовикипедия 
wiki.web.ru 
Поиск  
   Rambler's Top100 Service
 Главная страница  Конференции: Календарь / Материалы  Каталог ссылок    Словарь       Форумы        В помощь студенту     Последние поступления
   Геология | Курсы лекций
 Обсудить в форуме  Добавить новое сообщение
Вперед Вверх Назад Содержание Предметный указатель
Вперед: 12.2.2 Метод Полларда Вверх: 12.2 Факторизация чисел с экспоненциальной сложностью Назад: 12.2 Факторизация чисел с экспоненциальной сложностью   Содержание   Предметный указатель

12.2.1 Алгоритм Шермана -- Лемана

Этот алгоритм имеет оценку сложности $ O(n^{1/3})$ и заключается в следующем.     1. Считая, что $ n>8$, последовательно проверяем делимость исходного числа $ n$ на $ i=2,3,\ldots,\left[n^{1/3}\right]$.

    2. Если на этапе 1 делитель не найден и $ n$ составное, то $ n=pq$, где $ p$ и $ q$ -- простые числа, причем $ n^{1/3}<p\leqslant q<n^{2/3}$. Тогда для каждых $ k=1,2,\ldots,\left[n^{1/3}\right]$ и $ d=0,1,\ldots,\left[n^{1/6}\left/\left(4\sqrt k\right)\right.\right]+1$ полагаем $ a=\left[\sqrt{4kn}\right]+d$ и проверяем, является ли число $ a^2-4kn$ квадратом натурального числа. 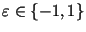Если да, то $ a^2\equiv b^2\mkern5mu({\rm mod}\,\,n)$, где $ b=\sqrt{a^2-4kn}$, поэтому если $ 1<(a-\varepsilon b,n)<n$ для некоторого $ \varepsilon\in\{-1,1\}$, то $ (a-\varepsilon b,n)$ -- искомый нетривиальный делитель $ n$.

Теорема 2.  Если алгоритм Шермана -- Лемана закончил работу и не нашел делителя $ n$, то $ n$ -- простое число.

Отметим, что в алгоритме Шермана -- Лемана возможны параллельные вычисления.

Вперед Вверх Назад Содержание Предметный указатель
Вперед: 12.2.2 Метод Полларда Вверх: 12.2 Факторизация чисел с экспоненциальной сложностью Назад: 12.2 Факторизация чисел с экспоненциальной сложностью   Содержание   Предметный указатель

Проект осуществляется при поддержке:
 Геологического факультета МГУ,
РФФИ
    
TopList Rambler's Top100