




Вперед: 12.3.5 Другие методы
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3.3 Алгоритм Бриллхарта - Моррисона
Содержание
Предметный указатель
Это один из самых широко используемых на практике методов.
Его описание можно найти в работах [Pom85],
[Silv]. Оценка сложности составляет
 ,
если используется гауссово исключение, и ,
если используется гауссово исключение, и  , если
используется метод Копперсмита -- Винограда. Стратегии PS
и EAS не используются, так как выбор значений , если
используется метод Копперсмита -- Винограда. Стратегии PS
и EAS не используются, так как выбор значений  происходит с помощью специального просеивания.
происходит с помощью специального просеивания.
Схема алгоритма заключается в следующем. Пусть 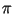 --
факторная база (т. е. конечное множество не слишком
больших простых чисел), --
факторная база (т. е. конечное множество не слишком
больших простых чисел),
![$ H(m)=m+\left[\sqrt{n\vphantom{n_1}}\right]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1573.gif) , а , а
 . Будем просеивать значения . Будем просеивать значения  , чтобы
отыскать те, для которых , чтобы
отыскать те, для которых 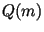 разлагается в произведение
простых чисел из факторной базы разлагается в произведение
простых чисел из факторной базы 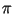 . Для этого:
1)
для каждого . Для этого:
1)
для каждого 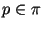 находим некоторые находим некоторые  и
и  такие, что такие, что
 для для
 ; ;
2)
заводим массив, пронумерованный значениями
целочисленной переменной  из достаточно большого
интервала из достаточно большого
интервала ![$ [-M,M]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1579.gif) , и для каждого , и для каждого  в в  -й элемент
массива помещаем достаточно грубо вычисленное значение -й элемент
массива помещаем достаточно грубо вычисленное значение
 ; ;
3)
для каждого 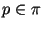 из элементов нашего
массива с номерами из элементов нашего
массива с номерами  такими, что такими, что
 или или
 , вычитаем достаточно
грубо вычисленное значение , вычитаем достаточно
грубо вычисленное значение  . После такой процедуры
мы получим массив, в котором . После такой процедуры
мы получим массив, в котором  -й элемент есть грубо
вычисленное значение -й элемент есть грубо
вычисленное значение
 ,
где ,
где
 . .
Теперь мы отбираем те номера  , для которых , для которых  -е
элементы массива достаточно малы, и для них разлагаем
значения -е
элементы массива достаточно малы, и для них разлагаем
значения 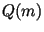 пробными делениями в произведение элементов
факторной базы. Используя технику этапов 3 и 4 алгоритма
Диксона, находим числа пробными делениями в произведение элементов
факторной базы. Используя технику этапов 3 и 4 алгоритма
Диксона, находим числа
 такие, что такие, что
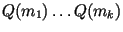 является квадратом натурального
числа, которое мы обозначим через является квадратом натурального
числа, которое мы обозначим через  . С другой стороны, . С другой стороны,
 .
Поэтому для .
Поэтому для
 имеем имеем
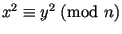 . Теперь если . Теперь если
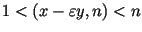 для некоторого для некоторого
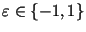 , то , то
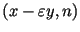 -- искомый нетривиальный делитель -- искомый нетривиальный делитель
 . .
Преимущество такого метода заключается в том, что на стадии
просеивания мы пользуемся только операцией вычитания и в
итоге отбрасываем большинство "плохих" (т. е. не
разлагающихся в произведение простых 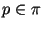 ) значений ) значений
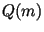 , в то время как в алгоритме Диксона "плохие" значения , в то время как в алгоритме Диксона "плохие" значения 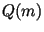 отбрасываются после деления на отбрасываются после деления на 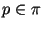 ,
что значительно дольше. ,
что значительно дольше.





Вперед: 12.3.5 Другие методы
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3.3 Алгоритм Бриллхарта - Моррисона
Содержание
Предметный указатель
|

