




Вперед: 13. Методы построения больших простых чисел
Вверх: 12. Задача факторизации больших целых чисел
Назад: 12.3.5 Другие методы
Содержание
Предметный указатель
12.4 Метод решета числового поля
В работе [LLMP] описан метод факторизации чисел  вида
вида
 , где , где  и и  невелики, с эвристической
оценкой сложности невелики, с эвристической
оценкой сложности
 , где , где
 . Этот метод
называется методом решета числового поля. С его помощью было разложено на
множители число . Этот метод
называется методом решета числового поля. С его помощью было разложено на
множители число
 . Суть метода
заключается в том, что мы переходим в некоторое
алгебраическое расширение . Суть метода
заключается в том, что мы переходим в некоторое
алгебраическое расширение
 поля рациональных
чисел поля рациональных
чисел
 и перебором и перебором
 , ,  , ищем
элементы , ищем
элементы  , которые разлагаются на множители в
некоторой факторной базе. Перебор , которые разлагаются на множители в
некоторой факторной базе. Перебор  и и  делается с
помощью специального просеивания, наподобие метода
квадратичного решета. Затем с помощью одного из методов
исключения находят соотношение делается с
помощью специального просеивания, наподобие метода
квадратичного решета. Затем с помощью одного из методов
исключения находят соотношение
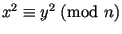 .
Тогда если .
Тогда если
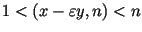 для некоторого для некоторого
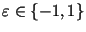 , то , то
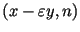 --
искомый нетривиальный делитель --
искомый нетривиальный делитель  . .
Имеется также препринт [BuhLP], в котором описан
алгоритм факторизации произвольного  со сложностью со сложностью
 арифметических операций. арифметических операций.
Имеются и другие работы в этом направлении
(см. [Adl91]).





Вперед: 13. Методы построения больших простых чисел
Вверх: 12. Задача факторизации больших целых чисел
Назад: 12.3.5 Другие методы
Содержание
Предметный указатель
|

