




Вперед: 13.4 Построение больших простых чисел n с использованием полного разложения n-1 на простые множители
Вверх: 13. Методы построения больших простых чисел
Назад: 13.2 Вероятностные тесты на простоту
Содержание
Предметный указатель
13.3 Простые числа специального вида
Здесь мы приведем ряд тестов для доказательства простоты
чисел специального вида.
Следующая теорема дает эффективно проверяемый критерий
простоты чисел вида  . .
Теорема 2 [Кнут,
 4.5.4]. Пусть 4.5.4]. Пусть  -- нечетное натуральное число, а -- нечетное натуральное число, а  .
Определим последовательность .
Определим последовательность  по формуле по формуле
 Тогда число
Тогда число  простое тогда и только тогда, когда простое тогда и только тогда, когда
 . .
Отметим, что числа вида  могут быть простыми только
при простом могут быть простыми только
при простом  , так как если , так как если  , то , то
 . Поэтому теорема 2 полезна только для
проверки простоты чисел вида . Поэтому теорема 2 полезна только для
проверки простоты чисел вида  , где , где  -- простое
число, т. е. для нахождения чисел Мерсенна (простых чисел
вида -- простое
число, т. е. для нахождения чисел Мерсенна (простых чисел
вида  ). Их в настоящее время известно немногим
более 30. ). Их в настоящее время известно немногим
более 30.
В работе [Will] предложены специальные тесты
для проверки простоты чисел вида  . Изучение этих
чисел продолжено в недавней работе [Gut]. В работе
[Wil2] специальные тесты предлагаются для чисел вида . Изучение этих
чисел продолжено в недавней работе [Gut]. В работе
[Wil2] специальные тесты предлагаются для чисел вида
 и и  , а в работе [Wil3] -- для чисел
вида , а в работе [Wil3] -- для чисел
вида  и и
 . В работе [BuCP]
изучаются простые числа вида . В работе [BuCP]
изучаются простые числа вида  и и
 . См. также работу [WilS], в
которой изучаются тесты простоты для чисел специального
вида. . См. также работу [WilS], в
которой изучаются тесты простоты для чисел специального
вида.
Имеются тесты, позволяющие строить пары простых чисел
специального вида.
Теорема 3 [Чеб].
Если  и и  -- простые числа, причем -- простые числа, причем  , то
1)
при , то
1)
при
  является первообразным
корнем по модулю является первообразным
корнем по модулю  ; ;
2)
при
  является первообразным
корнем по модулю является первообразным
корнем по модулю  . .
Таким образом, если  -- простое число, то для проверки
простоты -- простое число, то для проверки
простоты  достаточно проверить выполнение сравнений достаточно проверить выполнение сравнений
 для
для 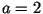 или или  (при (при
 или или
 соответственно). соответственно).
Работы [CP], [PSZ]
посвящены построению близнецов, т. е. пар простых чисел
 и и  . .
Заметим, что в данном разделе мы проверяли на простоту
числа  , для которых известно разложение , для которых известно разложение  или или  на простые множители. Общие методы построения больших
простых чисел, к описанию которых мы перейдем далее, также
существенно используют известное разложение
на простые множители. Общие методы построения больших
простых чисел, к описанию которых мы перейдем далее, также
существенно используют известное разложение  на
множители. на
множители.
Интересный метод построения больших простых чисел
специального вида предложен Пинцем, Стейгером и Семереди в
[PSS]. Справедлива следующая теорема.
Теорема 4.
Пусть  -- натуральное число вида -- натуральное число вида
 , где , где
 , ,
 . Тогда для простоты . Тогда для простоты  необходимо и
достаточно выполнения следующих двух условий:
1) необходимо и
достаточно выполнения следующих двух условий:
1)
 не является квадратом
целого неотрицательного числа; не является квадратом
целого неотрицательного числа;
2)
существует натуральное число  такое, что такое, что
 и и
Из этой теоремы следует такой способ построения больших
простых чисел.
1.
Выбрать  , где , где
 , ,
 , и положить , и положить
 . .
2.
Проверить условие 1) теоремы 4; если оно не
выполнено, то  составное. составное.
3.
Для всех натуральных  таких, что таких, что
 , проверять условие 2)
теоремы 4 ( , проверять условие 2)
теоремы 4 ( -- некоторая постоянная). Из
невыполнения этого условия может следовать, что -- некоторая постоянная). Из
невыполнения этого условия может следовать, что  составное. Если же при некотором
составное. Если же при некотором  условие 2) выполнено,
то условие 2) выполнено,
то  -- простое число. -- простое число.
Оценка сложности алгоритма --  арифметических
операций. арифметических
операций.
Важной отличительной чертой предложенного метода является
то, что при некотором значении  существует
бесконечно много простых чисел существует
бесконечно много простых чисел
 , простота
которых действительно устанавливается данным алгоритмом.
При этом количество таких , простота
которых действительно устанавливается данным алгоритмом.
При этом количество таких  , ,
 , оценивается
снизу величиной , оценивается
снизу величиной
 , где , где  -- также абсолютная постоянная.
-- также абсолютная постоянная.
В работе Гордона [Gor] обсуждается вопрос о построении
"сильных" простых чисел  , для которых , для которых  , ,
 , ,  , где , где  , ,  , , 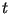 -- достаточно
большие простые числа. Такие -- достаточно
большие простые числа. Такие  важны, например, для
криптосистемы RSA. Доказано следующее утверждение: если важны, например, для
криптосистемы RSA. Доказано следующее утверждение: если
 , ,  -- различные нечетные простые числа, -- различные нечетные простые числа,  --
нечетное простое число, то --
нечетное простое число, то
 и и
 тогда и только тогда, когда тогда и только тогда, когда
 , где , где
 и и
 нечетно. Поэтому если нечетно. Поэтому если 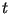 , ,  , ,  уже построены, то уже построены, то
 следует искать в прогрессии следует искать в прогрессии  , где , где  пробегает множество натуральных чисел. Однако автор
предлагает проверять простоту
пробегает множество натуральных чисел. Однако автор
предлагает проверять простоту  вероятностным способом.
Здесь можно предложить использовать методы, описываемые
ниже, поскольку известно частичное разложение вероятностным способом.
Здесь можно предложить использовать методы, описываемые
ниже, поскольку известно частичное разложение  на
множители. на
множители.





Вперед: 13.4 Построение больших простых чисел n с использованием полного разложения n-1 на простые множители
Вверх: 13. Методы построения больших простых чисел
Назад: 13.2 Вероятностные тесты на простоту
Содержание
Предметный указатель
|

