




Вперед: 13.6 Полиномиальные алгоритмы доказательства простоты n с помощью известного полного разложения n-1 на простые множители
Вверх: 13. Методы построения больших простых чисел
Назад: 13.4 Построение больших простых чисел n с использованием полного разложения n-1 на простые множители
Содержание
Предметный указатель
13.5 Построение больших простых чисел
с использованием частичного разложения
на множители
Справедлива следующая теорема [BriLS]:
Теорема 6.
Пусть  -- нечетное натуральное число, -- нечетное натуральное число,
 , где , где  -- взаимно простые
натуральные числа. Пусть -- взаимно простые
натуральные числа. Пусть  и
известно полное разложение и
известно полное разложение
 на простые множители.
Если для каждого на простые множители.
Если для каждого
 существует натуральное число
существует натуральное число  такое, что такое, что
 и и то
то  -- простое число. -- простое число.
На этой теореме основан следующий эффективный метод
построения больших простых чисел, который мы рекомендуем
для практического использования.
Будем индуктивно строить возрастающую последовательность
простых чисел
 до тех пор, пока не
построим число нужной величины. В качестве до тех пор, пока не
построим число нужной величины. В качестве  можно
взять любое известное простое число. Предположим, что можно
взять любое известное простое число. Предположим, что
 уже построено. Случайным образом выберем
натуральное число уже построено. Случайным образом выберем
натуральное число  из промежутка из промежутка
 . Пусть . Пусть  , где , где 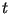 нечетно. Положим нечетно. Положим
 . Тогда . Тогда  , где , где
 , ,  ; так как ; так как
 , имеем , имеем  . Переберем несколько значений . Переберем несколько значений  , ,  , и
проверим для них условия теоремы 6 (здесь , и
проверим для них условия теоремы 6 (здесь  , ,
 , ,
 ). Если эти условия выполнены, то мы
полагаем ). Если эти условия выполнены, то мы
полагаем  . В противном случае следует выбрать другое
значение . В противном случае следует выбрать другое
значение  . .
Замечание.
Построив
 , уместно применить к нему
вероятностный метод Миллера -- Рабина (см. раздел 13.2); если окажется, что , уместно применить к нему
вероятностный метод Миллера -- Рабина (см. раздел 13.2); если окажется, что  составное, то
следует сразу перейти к выбору нового составное, то
следует сразу перейти к выбору нового  . .
Можно изменить процедуру построения  по по  в
вышеописанном алгоритме следующим образом. Если в
вышеописанном алгоритме следующим образом. Если
 , то случайно выбираем четное число , то случайно выбираем четное число  такое,
что такое,
что
 . Положим . Положим
 . Тогда . Тогда  , где , где  , ,
 ; кроме того, выполнено неравенство ; кроме того, выполнено неравенство
 , так как если , так как если
 , то , то
 , и мы пришли к противоречию. Поэтому согласно
теореме 6 для доказательства простоты , и мы пришли к противоречию. Поэтому согласно
теореме 6 для доказательства простоты  достаточно найти одно натуральное число
достаточно найти одно натуральное число  такое, что такое, что
 и и Если такое
Если такое  найдено, то мы полагаем найдено, то мы полагаем  . В противном
случае следует выбрать другое значение . В противном
случае следует выбрать другое значение  . .
Возможно дальнейшее уменьшение нижней границы для  в
теореме 6, например, до в
теореме 6, например, до
 (см. [BriLS]). Это приводит к дальнейшему
усовершенствованию указанного метода построения больших
простых чисел (см. [CQ]). (см. [BriLS]). Это приводит к дальнейшему
усовершенствованию указанного метода построения больших
простых чисел (см. [CQ]).
Существуют также методы (аналогичные описанным в
разделах 13.4 и 13.5) построения
больших простых чисел  с помощью полного или частичного
разложения с помощью полного или частичного
разложения  на множители (см. [BaWag]). на множители (см. [BaWag]).





Вперед: 13.6 Полиномиальные алгоритмы доказательства простоты n с помощью известного полного разложения n-1 на простые множители
Вверх: 13. Методы построения больших простых чисел
Назад: 13.4 Построение больших простых чисел n с использованием полного разложения n-1 на простые множители
Содержание
Предметный указатель
|

