




Вперед: 13.7.2 Алгоритм
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Содержание
Предметный указатель
Основную часть алгоритма можно описать следующим образом.
Предположим, что как-то удалось построить простое
число  и требуется построить еще большее простое число и требуется построить еще большее простое число
 . Это большее число ищется в виде . Это большее число ищется в виде
 |
(1) |
Можно, выбирая как-либо целые числа  , тестировать
появляющиеся числа , тестировать
появляющиеся числа  на простоту, например, с помощью
тестов, использующих знание частичного разложения на простоту, например, с помощью
тестов, использующих знание частичного разложения 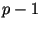 на
множители (см. раздел. 13.5). Для этого нужно,
чтобы число на
множители (см. раздел. 13.5). Для этого нужно,
чтобы число  , разложение которого на простые множители,
вообще говоря, считается неизвестным, было не очень большим
по сравнению с , разложение которого на простые множители,
вообще говоря, считается неизвестным, было не очень большим
по сравнению с  , скажем , скажем
 , где
возрастающая не очень быстро функция , где
возрастающая не очень быстро функция  описывается в
соответствующем тесте. Конструкция описывается в
соответствующем тесте. Конструкция  , естественно,
должна быть не уникальной, а обеспечивать получение
достаточно большого количества простых чисел в
прогрессии , естественно,
должна быть не уникальной, а обеспечивать получение
достаточно большого количества простых чисел в
прогрессии 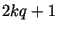 . Это достигается случайным выбором
начала отсчета -- четного числа . Это достигается случайным выбором
начала отсчета -- четного числа  на промежутке на промежутке
 , перебором чисел , перебором чисел
 и последующим
тестированием на простоту. Мы сейчас коротко обсудим
теоретические основы такого метода построения простых
чисел. и последующим
тестированием на простоту. Мы сейчас коротко обсудим
теоретические основы такого метода построения простых
чисел.
Прежде всего, согласно теореме Дирихле, доказанной еще в
1839 г., прогрессия (1) содержит бесконечное
количество простых чисел. Нас интересуют простые числа,
лежащие недалеко от начала прогрессии, ведь согласно
условиям тестирования должно выполняться ограничение
 . Оценка наименьшего простого числа в
арифметической прогрессии была получена еще в 1944 г. Ю. В. Линником. Она утверждает, что существует абсолютная
постоянная . Оценка наименьшего простого числа в
арифметической прогрессии была получена еще в 1944 г. Ю. В. Линником. Она утверждает, что существует абсолютная
постоянная  такая, что наименьшее простое число в
прогрессии (1) не превосходит такая, что наименьшее простое число в
прогрессии (1) не превосходит  . Постоянная . Постоянная  очень велика, заведомо выполняется неравенство
очень велика, заведомо выполняется неравенство
 . В предположении расширенной гипотезы Римана
о нулях L-функций Дирихле можно доказать (см. [Прах],
с. 272), что при любом . В предположении расширенной гипотезы Римана
о нулях L-функций Дирихле можно доказать (см. [Прах],
с. 272), что при любом
 наименьшее простое
число в прогрессии (1) не превосходит наименьшее простое
число в прогрессии (1) не превосходит
 . Таким образом, в
настоящее время никаких теоретических гарантий для
существования простого числа (1) с . Таким образом, в
настоящее время никаких теоретических гарантий для
существования простого числа (1) с  не
существует. Тем не менее опыт вычислений на ЭВМ показывает,
что простые числа в прогрессии встречаются достаточно
близко к ее началу. Упомянем в этой связи гипотезу о
существовании бесконечного количества простых чисел не
существует. Тем не менее опыт вычислений на ЭВМ показывает,
что простые числа в прогрессии встречаются достаточно
близко к ее началу. Упомянем в этой связи гипотезу о
существовании бесконечного количества простых чисел  с
условием, что число с
условием, что число  также простое (уже первый член
прогрессии (1) есть простое число). также простое (уже первый член
прогрессии (1) есть простое число).
Очень важен в связи с описываемым методом построения
простых чисел также вопрос о расстоянии между соседними
простыми числами в арифметической прогрессии. Ведь если это
расстояние велико, нет надежды обеспечить построение
большого количества простых  . Перебор чисел . Перебор чисел
 до того момента, как мы наткнемся на
простое до того момента, как мы наткнемся на
простое  , окажется слишком долгим. В более простом
вопросе о расстоянии между соседними простыми числами , окажется слишком долгим. В более простом
вопросе о расстоянии между соседними простыми числами
 и и  в натуральном ряде доказано лишь, что в натуральном ряде доказано лишь, что
 , что,
конечно же, слишком велико для наших целей. Вместе с тем,
существует так называемая гипотеза Крамера (1936 г.), что , что,
конечно же, слишком велико для наших целей. Вместе с тем,
существует так называемая гипотеза Крамера (1936 г.), что
 , дающая вполне
приемлемую оценку. Вычисления на ЭВМ показывают, что
простые числа в арифметических прогрессиях расположены
достаточно плотно. , дающая вполне
приемлемую оценку. Вычисления на ЭВМ показывают, что
простые числа в арифметических прогрессиях расположены
достаточно плотно.
В качестве итога обсуждения в этом пункте подчеркнем
следующее: если принять на веру, что наименьшее простое число, а
также расстояние между соседними простыми числами при
 в арифметической прогрессии (1) оцениваются
величиной в арифметической прогрессии (1) оцениваются
величиной
 , то предложенная схема
построения простых чисел имеет полиномиальную сложность.
Кроме того, несмотря на отсутствие теоретических оценок
времени работы алгоритмов, отыскивающих простые
числа в арифметических прогрессиях со сравнительно
большой разностью, на практике эти алгоритмы работают
вполне удовлетворительно. , то предложенная схема
построения простых чисел имеет полиномиальную сложность.
Кроме того, несмотря на отсутствие теоретических оценок
времени работы алгоритмов, отыскивающих простые
числа в арифметических прогрессиях со сравнительно
большой разностью, на практике эти алгоритмы работают
вполне удовлетворительно.





Вперед: 13.7.2 Алгоритм
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Содержание
Предметный указатель
|

