Все о геологии :: на главную страницу! Геовикипедия 
wiki.web.ru 
Поиск  
   Rambler's Top100 Service
 Главная страница  Конференции: Календарь / Материалы  Каталог ссылок    Словарь       Форумы        В помощь студенту     Последние поступления
   Геология | Курсы лекций
 Обсудить в форуме  Добавить новое сообщение
Вперед Вверх Назад Содержание Предметный указатель
Вперед: 13.8 Алгоритм построения простых чисел Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма" Назад: 13.7.5 Отсеивание составных чисел   Содержание   Предметный указатель

13.7.6 Замечания

1. Думается, что однозначный выбор числа $ p_s$, как наименьшего простого числа длиной в $ t_s$ битов, в пункте 3 Алгоритма значительно сужает множество выдаваемых Алгоритмом пар простых чисел $ p$ и $ q$. Очень просто организовать какой-либо случайный выбор $ p_s$ на интервале $ 2^{t_s-1}<p_s<2^{t_s}$, что расширит множество возможных чисел $ p$ примерно в 5714 раз. Например, можно, выбрав случайным образом целое число $ A$ на этом интервале, тестировать на простоту следующие за ним целые числа, проверяя их делимость на все простые, не превосходящие $ 2^8=256$, ведь $ t_s\leqslant 16$.

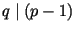2. В процессе работы Алгоритма можно контролировать не длину битовой записи числа -- достаточно грубую характеристику, а саму величину числа. Новый алгоритм, будет выдавать простое число $ p$, лежащее между двумя заданными границами $ X<p<Y$ и простой делитель $ q\mid(p-1)$, удовлетворяющий неравенствам

$\displaystyle \left\lceil\frac12\sqrt Y\right\rceil< q<\left[\sqrt Y\right]. $

Изменения в Алгоритме таковы.

В новом пункте 1 определить последовательность чисел

\begin{displaymath}\begin{aligned}X_0&=X,\\ X_{r+1}&=\left\lceil\frac12\sqrt{Y_r... ...egin{gathered}\null\\ 0\leqslant r\leqslant s-1, \end{gathered}\end{displaymath}

где число $ s$ выбрано так, что $ Y_s<2^{17}$.

В пункте 2 найти простое число $ p_s$, удовлетворяющее неравенствам $ X_s<p_s<Y_s$. Это можно сделать, перебирая все нечетные числа на указанном промежутке и проверяя их делимость на все простые, меньшие 362 (т. к. $ 363^2>2^{17}$).

Пункт 3 остается без изменений.

В пункте 4 число $ N$ вычисляется по формуле

$\displaystyle N=\left\lceil X_m/p_{m+1}\right\rceil+ \left[(X_m\cdot\xi)/p_{m+1}\right]. $

Пункты 5 и 6 остаются без изменений.

В пункте 7 должно стоять неравенство $ p_m\geqslant Y_m$.

Остальные пункты Алгоритма остаются без изменений.

Проверим по индукции, что в процессе работы нового алгоритма строятся простые числа

$\displaystyle p_s,\ldots,p_1,p_0, $

удовлетворяющие неравенствам

$\displaystyle X_m<p_m<Y_m,\qquad 0\leqslant m\leqslant s.$ (10)

При $ m=s$ это следует из пункта 2 нового алгоритма. Из новых пунктов 4, 6 и 7 следуют неравенства

$\displaystyle p_m>(N+u)p_{m+1}\geqslant\frac{X_m}{p_{m+1}}\cdot p_{m+1}=X+m,\qquad p_m<Y_m, $

что доказывает (10).

С помощью неравенств (10), определения последовательностей $ X_i$, $ Y_i$ и пункта 7 нового алгоритма находим

$\displaystyle N+u=\frac{p_m-1}{p_{m+1}}<\frac{Y_m}{p_{m+1}}< \frac{Y_m}{X_{m+1}}\leqslant 4X_{m+1}<4p_{m+1}. $

Таким образом, если $ p_{m+1}$ -- простое число, то для $ q=p_{m+1}$, $ p=p_m$, $ 2k=N+u$ выполнены условия теоремы 8 и можно утверждать, что число $ p_m$ также простое.

Если внести в Алгоритм изменения пункта 8.7, то в (9) можно несколько расширить интервал возможных значений чисел $ p_m$, положив

$\displaystyle X_{r+1}=\left\lceil\sqrt{Y_r/8}\right\rceil. $

3. Предлагаемый Стандартом Алгоритм построения больших простых чисел предполагает наличие у пользователя арифметики многократной точности -- специального набора программ, осуществляющих арифметические операции (сложение и вычитание, умножение и деление, вычисления по модулю длинного простого) с целыми числами большой длины (до 1024 битов). Отсутствие таких программ может сделать Стандарт просто бесполезным. А несовершенство этой части может привести пользователей Стандарта как к значительным потерям машинного времени, так и к ошибочным результатам. Поэтому представляется совершенно необходимым сертифицировать некоторый набор алгоритмов и программ, осуществляющих вычисления с числами большой длины.

Вперед Вверх Назад Содержание Предметный указатель
Вперед: 13.8 Алгоритм построения простых чисел Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма" Назад: 13.7.5 Отсеивание составных чисел   Содержание   Предметный указатель

Проект осуществляется при поддержке:
 Геологического факультета МГУ,
РФФИ
    
TopList Rambler's Top100