




Вперед: 15.3 Интерактивные системы доказательства с нулевым разглашением
Вверх: 15. Основные понятия теории доказательств с нулевым разглашением
Назад: 15.1 Введение
Содержание
Предметный указатель
15.2 Интерактивные системы доказательства
Теория доказательств с нулевым разглашением базируется на
понятии интерактивной системы доказательства (interactive
proof system), которое было введено в 1985 году независимо в
работах Бабаи [Bab] (окончательный вариант
[BMo]) и Гольдвассер, Микали и Ракоффа [GMR1]
(окончательный вариант [GMR2]). К настоящему времени
это понятие стало предметом изучения довольно
представительной ветви теории сложности вычислений, имеющей
глубокие связи с другими разделами теории.
Мы предполагаем известными понятия детерминированной и
недетерминированной машины Тьюринга (см. [ГДж],
[АХУ]) и языка, распознаваемого детерминированной или
недетерминированной машиной. Для единообразия обозначений
везде в этом подразделе мы будем обозначать через  язык
в двоичном алфавите, т. е. произвольное множество,
состоящее из конечных строк из нулей и единиц. Через язык
в двоичном алфавите, т. е. произвольное множество,
состоящее из конечных строк из нулей и единиц. Через  или
или  мы будем обозначать слово в том же алфавите,
которое подается на вход машины Тьюринга, а через мы будем обозначать слово в том же алфавите,
которое подается на вход машины Тьюринга, а через  --
его длину. Время работы детерминированной
(недетерминированной) машины Тьюринга на входе --
его длину. Время работы детерминированной
(недетерминированной) машины Тьюринга на входе  -- это
(максимально возможное) количество тактов ее работы на этом
входе. Если существует некоторый полином, который
ограничивает сверху время работы машины Тьюринга на входах
длины -- это
(максимально возможное) количество тактов ее работы на этом
входе. Если существует некоторый полином, который
ограничивает сверху время работы машины Тьюринга на входах
длины  для всех достаточно больших для всех достаточно больших  , то машину будем
называть полиномиальной. Языки, которые распознаются полиномиальными
детерминированными (недетерминированными) машинами
Тьюринга, образуют класс P
(NP). , то машину будем
называть полиномиальной. Языки, которые распознаются полиномиальными
детерминированными (недетерминированными) машинами
Тьюринга, образуют класс P
(NP).
Память, которая расходуется детерминированной машиной
Тьюринга на входе  -- это количество ячеек рабочей
ленты, используемых в ходе работы машины на этом входном
слове. Если она (память) ограничена полиномом от -- это количество ячеек рабочей
ленты, используемых в ходе работы машины на этом входном
слове. Если она (память) ограничена полиномом от  , то
язык, распознаваемый этой машиной, по определению,
принадлежит классу PSPACE. , то
язык, распознаваемый этой машиной, по определению,
принадлежит классу PSPACE.
Эквивалентное определение класса NP следующее.
Язык  принадлежит классу NP тогда и только тогда, когда
существует двуместный предикат принадлежит классу NP тогда и только тогда, когда
существует двуместный предикат  , определенный на таких
парах слов , определенный на таких
парах слов  и и 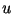 , что длина , что длина 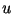 ограничена некоторым
полиномом от длины ограничена некоторым
полиномом от длины  , и вычислимый полиномиальной
детерминированной машиной Тьюринга, такой что , и вычислимый полиномиальной
детерминированной машиной Тьюринга, такой что
 Класс coNP состоит в точности из языков, дополнения к
которым лежат в классе NP, и также может быть определен
вышеизложенным способом с помощью соотношения
Класс coNP состоит в точности из языков, дополнения к
которым лежат в классе NP, и также может быть определен
вышеизложенным способом с помощью соотношения

В нашем дальнейшем изложении встречаются понятия
NP-полного и PSPACE-полного
языка. Язык  называется полным в
классе называется полным в
классе  , если он принадлежит этому классу и для любого
языка , если он принадлежит этому классу и для любого
языка  из класса из класса  существует функция существует функция  , вычислимая
детерминированной полиномиальной машиной Тьюринга и такая,
что для произвольного , вычислимая
детерминированной полиномиальной машиной Тьюринга и такая,
что для произвольного 
 Таким образом, вопрос о существовании какой-либо
эффективной процедуры для всех языков из класса
Таким образом, вопрос о существовании какой-либо
эффективной процедуры для всех языков из класса  сводится к вопросу о существовании этой процедуры для
сводится к вопросу о существовании этой процедуры для
 -полного языка. -полного языка.
Вероятностная машина Тьюринга -- это обычная (детерминированная) машина
Тьюринга, снабженная дополнительной лентой, на которой
записывается случайное слово. Говоря неформально, машина
имеет возможность подбрасывать монету и совершать то или
иное действие в зависимости от результата. Вероятностная
машина Тьюринга распознает язык  , если на входе , если на входе
 она выдает положительный ответ с вероятностью не
менее она выдает положительный ответ с вероятностью не
менее  , а на входе , а на входе  с вероятностью не более с вероятностью не более
 , где вероятность берется по равномерному
распределению случайных слов (одинаковой длины). Таким
образом, вероятность ошибочного ответа машины на любом
входе не превосходит , где вероятность берется по равномерному
распределению случайных слов (одинаковой длины). Таким
образом, вероятность ошибочного ответа машины на любом
входе не превосходит  . .
Класс BPP содержит языки, распознаваемые
вероятностными машинами Тьюринга с полиномиальным
ограничением на время работы. Важно отметить, что по всякой
полиномиальной вероятностной машине Тьюринга  можно
построить полиномиальную вероятностную машину можно
построить полиномиальную вероятностную машину  ,
распознающую тот же язык, но с вероятностью ошибки менее
чем ,
распознающую тот же язык, но с вероятностью ошибки менее
чем
 для заданного полинома для заданного полинома  . Программа
работы машины . Программа
работы машины  следующая. На входе следующая. На входе   раз моделируется работа машины
раз моделируется работа машины  на этом же входе, каждый
раз с независимым выбором случайного слова. Ответ машины на этом же входе, каждый
раз с независимым выбором случайного слова. Ответ машины
 совпадает с наиболее часто встречающимся ответом в
моделированиях работы машины совпадает с наиболее часто встречающимся ответом в
моделированиях работы машины  . .
Интерактивная система доказательства -- это игра двух участников,
которых мы будем называть игроками  (Prover), или
доказывающим, и (Prover), или
доказывающим, и  (Verifier), или
проверяющим. Перед игрой формулируется
некоторое утверждение (Verifier), или
проверяющим. Перед игрой формулируется
некоторое утверждение  (например, что некоторый объект (например, что некоторый объект
 обладает свойством обладает свойством  ). В ходе игры ). В ходе игры  и и  обмениваются сообщениями. В конце игры игрок
обмениваются сообщениями. В конце игры игрок  выносит
окончательное решение, является ли выносит
окончательное решение, является ли  истинным или же
ложным. Цель игрока истинным или же
ложным. Цель игрока  -- убедить игрока -- убедить игрока  в том, что в том, что
 истинно. При этом игрок истинно. При этом игрок  может мошенничать и целью
игрока может мошенничать и целью
игрока  является проверка аргументов игрока является проверка аргументов игрока  . Игрок . Игрок
 имеет ограниченные вычислительные возможности, а именно
-- время его работы ограничено некоторым полиномом от длины имеет ограниченные вычислительные возможности, а именно
-- время его работы ограничено некоторым полиномом от длины
 , и самостоятельно, без помощи игрока , и самостоятельно, без помощи игрока  , он не способен
распознать истинность утверждения , он не способен
распознать истинность утверждения  . Вычислительные
возможности игрока . Вычислительные
возможности игрока  никак не ограничиваются, что в
действительности может соответствовать ситуации, когда никак не ограничиваются, что в
действительности может соответствовать ситуации, когда  владеет какой-то трудно получаемой информацией (хотя,
напомним, он может и блефовать, утверждая, что такая
информация у него имеется). Таким образом, программа
действий игрока
владеет какой-то трудно получаемой информацией (хотя,
напомним, он может и блефовать, утверждая, что такая
информация у него имеется). Таким образом, программа
действий игрока  должна быть устроена так, что
во-первых, в случае должна быть устроена так, что
во-первых, в случае  -- истинно, игрок -- истинно, игрок  может убедить игрока
может убедить игрока  признать это; признать это;
во-вторых, в случае  -- ложно, игрок -- ложно, игрок  не
сможет убедить не
сможет убедить  в противном, какие бы аргументы он не
выдвигал (т. е., вне зависимости от получаемых от в противном, какие бы аргументы он не
выдвигал (т. е., вне зависимости от получаемых от  сообщений,
сообщений,  в этом случае делает вывод, что в этом случае делает вывод, что  ложно). ложно).
Добавим, что игроки  и и  в ходе игры могут
подбрасывать монету (каждый свою и втайне друг от друга), и
использовать результаты этих подбрасываний при выполнении
своих действий. Мы допускаем, что игрок в ходе игры могут
подбрасывать монету (каждый свою и втайне друг от друга), и
использовать результаты этих подбрасываний при выполнении
своих действий. Мы допускаем, что игрок  может иногда
ошибаться, но требуем, чтобы вероятность принятия им
неправильного решения была пренебрежимо малой. может иногда
ошибаться, но требуем, чтобы вероятность принятия им
неправильного решения была пренебрежимо малой.
Формализацию описанной модели мы приводим ниже, после
неформального обсуждения и примеров.
Пусть  -- это утверждение вида -- это утверждение вида  , где , где  --
слово, а --
слово, а  -- язык в двоичном алфавите. Если существует
интерактивная система для доказательства утверждений такого
сорта, то мы говорим, что язык -- язык в двоичном алфавите. Если существует
интерактивная система для доказательства утверждений такого
сорта, то мы говорим, что язык  обладает интерактивной
системой доказательства (или протоколом интерактивного
доказательства, или просто интерактивным доказательством).
Из пока неформального определения интерактивного
доказательства вытекает, что языки из классов NP и BPP
обладают довольно простыми интерактивными доказательствами.
В случае языка из NP игрок обладает интерактивной
системой доказательства (или протоколом интерактивного
доказательства, или просто интерактивным доказательством).
Из пока неформального определения интерактивного
доказательства вытекает, что языки из классов NP и BPP
обладают довольно простыми интерактивными доказательствами.
В случае языка из NP игрок  моделирует детерминированным
образом работу полиномиальной недетерминированной машины
Тьюринга, запросив подсказку у игрока моделирует детерминированным
образом работу полиномиальной недетерминированной машины
Тьюринга, запросив подсказку у игрока  . Такой подсказкой
может служить так называемая догадка (witness) для входного
слова. Например, если входным словом является формула
пропозиционального исчисления, выполнимость которой
требуется распознать, то догадкой является набор значений
аргументов, на котором эта формула истинна. Подчеркнем,
что игрок . Такой подсказкой
может служить так называемая догадка (witness) для входного
слова. Например, если входным словом является формула
пропозиционального исчисления, выполнимость которой
требуется распознать, то догадкой является набор значений
аргументов, на котором эта формула истинна. Подчеркнем,
что игрок  имеет неограниченные вычислительные
возможности и поэтому он всегда может найти требуемый набор
значений аргументов, если только такой существует. В случае
языка из BPP игрок имеет неограниченные вычислительные
возможности и поэтому он всегда может найти требуемый набор
значений аргументов, если только такой существует. В случае
языка из BPP игрок  непосредственно моделирует работу
соответствующей полиномиальной вероятностной машины
Тьюринга и не нуждается в подсказках игрока непосредственно моделирует работу
соответствующей полиномиальной вероятностной машины
Тьюринга и не нуждается в подсказках игрока  . .
Первый нетривиальный пример интерактивного доказательства
был предложен в [GMR1] для языка КВАДРАТИЧНЫЕ НЕВЫЧЕТЫ
(QUADRATIC NONRESIDUE, сокращенно QNR), состоящего из таких
пар  взаимно простых натуральных чисел, что взаимно простых натуральных чисел, что  и и
 не является квадратичным вычетом по модулю не является квадратичным вычетом по модулю  , т. е. не существует , т. е. не существует  такого, что такого, что
 .
Положим .
Положим
![$ n=[\log x+\log y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img2055.gif) . Ниже мы считаем, что
умножение происходит в группе . Ниже мы считаем, что
умножение происходит в группе
 натуральных
чисел, меньших чем натуральных
чисел, меньших чем  и взаимно простых с ним. Пересылку
сообщения и взаимно простых с ним. Пересылку
сообщения  от игрока от игрока  игроку игроку  мы будем записывать мы будем записывать
 , а сообщения , а сообщения 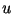 от игрока от игрока  игроку
игроку  -- как -- как
 . На входе . На входе  (т. е.,
(т. е.,  -- это утверждение -- это утверждение
 QNR), игра
происходит следующим образом: QNR), игра
происходит следующим образом:
Таким образом, игрок  втайне от втайне от  подбросил монету подбросил монету  раз, получив последовательность
раз, получив последовательность
 .
Далее, по каждому биту .
Далее, по каждому биту
 он вычисляет,
опять используя случайность, число он вычисляет,
опять используя случайность, число  и посылает эти
числа игроку и посылает эти
числа игроку  , требуя, чтобы тот восстановил исходную
последовательность , требуя, чтобы тот восстановил исходную
последовательность
 .
Заметим теперь, что в случае .
Заметим теперь, что в случае
 QNR значения QNR значения
 определяются однозначно по значениям определяются однозначно по значениям  ,
а именно ,
а именно
 тогда и только тогда, когда тогда и только тогда, когда
 -- квадратичный вычет по модулю -- квадратичный вычет по модулю  .
Следовательно, в этом случае игрок .
Следовательно, в этом случае игрок  может вычислить может вычислить
 и тем самым убедить игрока и тем самым убедить игрока  дать
положительный ответ (с вероятностью дать
положительный ответ (с вероятностью 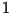 ). Если же ). Если же
 QNR, то QNR, то  , которые получает , которые получает  , --
это просто случайные квадратичные вычеты по модулю , --
это просто случайные квадратичные вычеты по модулю  , и
понятно, что какую бы последовательность , и
понятно, что какую бы последовательность  не
послал игрок не
послал игрок  , для каждого конкретного , для каждого конкретного 
 с вероятностью с вероятностью  , а значит для всех , а значит для всех
 равенство равенство
 будет выполнено с
вероятностью будет выполнено с
вероятностью  . Таким образом, если . Таким образом, если
 QNR, то игрок QNR, то игрок  выдаст положительный ответ лишь с этой
экспоненциально малой вероятностью. выдаст положительный ответ лишь с этой
экспоненциально малой вероятностью.
Следующий пример эксплуатирует по существу ту же идею и
появился в работе Гольдрайха, Микали и Вигдерсона
[GMW1] (окончательный вариант [GMW2]). Теперь мы
опишем интерактивную систему доказательства для языка
НЕИЗОМОРФИЗМ ГРАФОВ (GRAPH NONISOMORPHISM, сокращенно GNI),
состоящего из всех пар  и и  неизоморфных между
собой графов. Графы называются изоморфными, если существует
взаимно однозначное соответствие между их вершинами, при
котором соединенным ребром вершинам в одном графе
соответствуют соединенные вершины в другом графе. Очевидно,
не упрощая задачи, мы можем предполагать, что неизоморфных между
собой графов. Графы называются изоморфными, если существует
взаимно однозначное соответствие между их вершинами, при
котором соединенным ребром вершинам в одном графе
соответствуют соединенные вершины в другом графе. Очевидно,
не упрощая задачи, мы можем предполагать, что  и и
 -- это графы на одном и том же множестве вершин -- это графы на одном и том же множестве вершин
 мощности мощности  . .
Как легко видеть, все рассуждения, которые мы провели для
интерактивной системы для языка QNR, с очевидными
изменениями остаются в силе и для описанной системы для
GNI.
Ниже мы даем определение интерактивной системы
доказательства
 для языка для языка  , введенное
Гольдвассер, Микали и Ракоффом [GMR1]. , введенное
Гольдвассер, Микали и Ракоффом [GMR1].
Пусть  -- полиномиальная вероятностная машина Тьюринга; -- полиномиальная вероятностная машина Тьюринга;
 -- вероятностная машина Тьюринга без ограничений на
сложность. Машины -- вероятностная машина Тьюринга без ограничений на
сложность. Машины  и и  имеют общую входную ленту, на
которой записывается входное слово имеют общую входную ленту, на
которой записывается входное слово  , и с которой они
могут только считывать информацию. Кроме того, они имеют
общую ленту для обмена сообщениями. Каждая из машин , и с которой они
могут только считывать информацию. Кроме того, они имеют
общую ленту для обмена сообщениями. Каждая из машин  и и
 считывает предыдущую запись, сделанную другой из них, и
делает собственную очередную запись (т. е., машины считывает предыдущую запись, сделанную другой из них, и
делает собственную очередную запись (т. е., машины  и и
 работают в режиме диалога -- после отправки сообщения
каждая из них переходит в состояние ожидания до получения
ответа). Под очередным раундом мы понимаем
очередную передачу сообщения машиной работают в режиме диалога -- после отправки сообщения
каждая из них переходит в состояние ожидания до получения
ответа). Под очередным раундом мы понимаем
очередную передачу сообщения машиной  машине машине  , а
затем и сообщения машины , а
затем и сообщения машины  машине машине  (или наоборот, в
зависимости от того, кто согласно протоколу инициирует
диалог). Если в результате описанных обменов сообщениями
машина (или наоборот, в
зависимости от того, кто согласно протоколу инициирует
диалог). Если в результате описанных обменов сообщениями
машина  останавливается в принимающем состоянии (выдает
положительный ответ), то мы говорим, что останавливается в принимающем состоянии (выдает
положительный ответ), то мы говорим, что  убеждает
убеждает  . .
Система
 является интерактивной системой
доказательства для языка является интерактивной системой
доказательства для языка  (представляет
интерактивный протокол для (представляет
интерактивный протокол для
 , распознает язык , распознает язык  ), если выполнены следующие
условия:
1)
если ), если выполнены следующие
условия:
1)
если  , то , то  убеждает
убеждает  с вероятностью не
менее с вероятностью не
менее  , ,
2)
если  , то какова бы ни была
машина , то какова бы ни была
машина  , она убеждает , она убеждает  с вероятностью не более чем с вероятностью не более чем
 .
В литературе по интерактивным протоколам условие 1
называется полнотой
(completeness), а условие 2 --
корректностью (soundness)
протокола. .
В литературе по интерактивным протоколам условие 1
называется полнотой
(completeness), а условие 2 --
корректностью (soundness)
протокола.
На языке приведенного выше неформального описания машины
 и и  -- это игроки -- это игроки  и и  . Если для некоторого
языка задана интерактивная система . Если для некоторого
языка задана интерактивная система
 , то игрок , то игрок  в отличие от
в отличие от  будет называться честным.
Класс языков, обладающих интерактивными системами
доказательства, обозначается IP. Класс языков, для которых
существуют интерактивные системы с ограничением будет называться честным.
Класс языков, обладающих интерактивными системами
доказательства, обозначается IP. Класс языков, для которых
существуют интерактивные системы с ограничением  на
количество раундов, обозначается IP на
количество раундов, обозначается IP . Здесь . Здесь  -- некоторая функция от длины входа, которая, очевидно, не
может превышать время работы машины
-- некоторая функция от длины входа, которая, очевидно, не
может превышать время работы машины  и, следовательно,
ограничена некоторым полиномом от и, следовательно,
ограничена некоторым полиномом от  . .
Замечания
1. Как вытекает из определения, очередное сообщение
 игрока игрока  игроку игроку  зависит от входного слова зависит от входного слова
 , сообщений , сообщений
 , полученных в
предыдущих раундах от игрока , полученных в
предыдущих раундах от игрока  , и от результатов , и от результатов  подбрасывания монеты игроком
подбрасывания монеты игроком  . Отметим, что . Отметим, что
 -- полиномиально
вычислимая функция. Очередное сообщение -- полиномиально
вычислимая функция. Очередное сообщение  игрока игрока  является функцией произвольной сложности от входного слова
является функцией произвольной сложности от входного слова
 , уже полученных им от игрока , уже полученных им от игрока  сообщений сообщений
 , и результатов подбрасывания
собственной монеты. Окончательный ответ игрока , и результатов подбрасывания
собственной монеты. Окончательный ответ игрока  является
значением полиномиально вычислимого предиката является
значением полиномиально вычислимого предиката
 . .
2. Интерактивная система
 может быть задана
только программой игрока может быть задана
только программой игрока  . Честного игрока . Честного игрока  можно
определить требованием следовать оптимальной стратегии,
чтобы убедить можно
определить требованием следовать оптимальной стратегии,
чтобы убедить  . Таким образом, можно в частности
считать, что . Таким образом, можно в частности
считать, что  -- детерминированная машина Тьюринга.
Однако возможность делать случайный выбор будет существенна
в определении систем доказательства с нулевым разглашением. -- детерминированная машина Тьюринга.
Однако возможность делать случайный выбор будет существенна
в определении систем доказательства с нулевым разглашением.
3. Из определения вытекает, что если
 --
интерактивная система доказательства для некоторого языка,
то как количество раундов, так и длины сообщений, которыми
обмениваются --
интерактивная система доказательства для некоторого языка,
то как количество раундов, так и длины сообщений, которыми
обмениваются  и и  заведомо не превосходят времени
работы машины заведомо не превосходят времени
работы машины  и, следовательно, ограничены некоторым
полиномом от и, следовательно, ограничены некоторым
полиномом от  . .
4. Как вытекает из пунктов 1 и 2 определения, мы
допускаем вероятность ошибки не более чем  .
Определение останется эквивалентным исходному, даже если мы
потребуем ограничить вероятность ошибки экспоненциально
малой величиной, скажем .
Определение останется эквивалентным исходному, даже если мы
потребуем ограничить вероятность ошибки экспоненциально
малой величиной, скажем
 для некоторой
константы для некоторой
константы 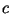 . Это следует из возможности применения
стандартного преобразования вероятностного алгоритма,
описанного в разделе 15.2, и легко усматривается из
приведенных выше примеров. При этом не обязательно
увеличивать количество раундов протокола. Независимые
выполнения протокола можно организовать параллельно, т. е. в очередной раунд передавать несколько экземпляров
независимых сообщений (как в описанных выше протоколах для
языков КВАДРАТИЧНЫЕ НЕВЫЧЕТЫ и НЕИЗОМОРФИЗМ ГРАФОВ). В этом
случае увеличивается в полиномиальное число раз только
длина передаваемых сообщений. . Это следует из возможности применения
стандартного преобразования вероятностного алгоритма,
описанного в разделе 15.2, и легко усматривается из
приведенных выше примеров. При этом не обязательно
увеличивать количество раундов протокола. Независимые
выполнения протокола можно организовать параллельно, т. е. в очередной раунд передавать несколько экземпляров
независимых сообщений (как в описанных выше протоколах для
языков КВАДРАТИЧНЫЕ НЕВЫЧЕТЫ и НЕИЗОМОРФИЗМ ГРАФОВ). В этом
случае увеличивается в полиномиальное число раз только
длина передаваемых сообщений.
Выше были отмечены включения сложностных классов NP и BPP в
класс IP и доказано, что языки QNR и GNI тоже лежат в
IP и доказано, что языки QNR и GNI тоже лежат в
IP . Для языка QNR известно его включение в класс
NP . Для языка QNR известно его включение в класс
NP coNP, вопрос о принадлежности языка GNI классам
NP или BPP открыт. coNP, вопрос о принадлежности языка GNI классам
NP или BPP открыт.
Естественным образом возникает вопрос: какие языки
обладают интерактивными системами доказательства, т. е. каков объем класса IP. Долгое время об этом ничего не было
известно, кроме несложно устанавливаемых соотношений
NP BPP BPP IP IP PSPACE PSPACE Полностью вопрос был решен в 1989 году в работах Фортноу,
Карлоффа, Лунда и Нисана [FKLN] и Шамира [Sha],
где была предложена интерактивная система доказательства
для PSPACE-полного множества. Отсюда следует, что
интерактивными доказательствами обладают в точности языки,
распознаваемые с полиномиально ограниченной памятью.
Полностью вопрос был решен в 1989 году в работах Фортноу,
Карлоффа, Лунда и Нисана [FKLN] и Шамира [Sha],
где была предложена интерактивная система доказательства
для PSPACE-полного множества. Отсюда следует, что
интерактивными доказательствами обладают в точности языки,
распознаваемые с полиномиально ограниченной памятью.
Теорема 1.
IP PSPACE. PSPACE.
Упрощенное доказательство этого факта предложено в
[She].
Таким образом, оказалось, что интерактивные системы
доказательства имеют довольно большие возможности. Можно
даже сказать, что этот результат был в достаточной степени
неожиданным: до его появления многие исследователи считали,
что класс IP не может быть значительно шире класса NP (хотя
соотношение между классами NP и PSPACE до сих пор не
выяснено, представляется правдоподобным, что класс PSPACE
существенно шире).





Вперед: 15.3 Интерактивные системы доказательства с нулевым разглашением
Вверх: 15. Основные понятия теории доказательств с нулевым разглашением
Назад: 15.1 Введение
Содержание
Предметный указатель
|

