




Вперед: Литература
Вверх: 15. Основные понятия теории доказательств с нулевым разглашением
Назад: 15.2 Интерактивные системы доказательства
Содержание
Предметный указатель
15.3 Интерактивные системы доказательства с нулевым
разглашением
Предположим, что задана интерактивная система
 , где игрок , где игрок  доказывает игроку доказывает игроку  истинность
утверждения истинность
утверждения  , состоящего, например, в том, что некоторые
графы , состоящего, например, в том, что некоторые
графы  и и  изоморфны. Для достижения своей
цели игрок изоморфны. Для достижения своей
цели игрок  может просто предъявить игроку может просто предъявить игроку  изоморфизм между
изоморфизм между  и и  , который игрок , который игрок  самостоятельно вычислить не в состоянии и хотел бы получить
от игрока
самостоятельно вычислить не в состоянии и хотел бы получить
от игрока  . Предположим однако, что предоставление
игроку . Предположим однако, что предоставление
игроку  столь исчерпывающей информации не в интересах
игрока столь исчерпывающей информации не в интересах
игрока  и он хотел бы сохранить ее в секрете. Таким
образом, цель игрока и он хотел бы сохранить ее в секрете. Таким
образом, цель игрока  -- убедить игрока -- убедить игрока  , что
заданные графы изоморфны, не выдав при этом никаких
полезных сведений, которые игрок , что
заданные графы изоморфны, не выдав при этом никаких
полезных сведений, которые игрок  не мог бы получить
самостоятельно. Более того, мы хотим, чтобы эта цель
достигалась даже если игрок не мог бы получить
самостоятельно. Более того, мы хотим, чтобы эта цель
достигалась даже если игрок  имеет дело с любым другим
игроком имеет дело с любым другим
игроком  (с полиномиально ограниченными
возможностями), задавшимся целью получить от (с полиномиально ограниченными
возможностями), задавшимся целью получить от  как можно
больше сведений. Оказывается, можно разработать протокол как можно
больше сведений. Оказывается, можно разработать протокол
 , являющийся интерактивным доказательством в
смысле определения из раздела 15.2 и дополнительно
учитывающий эти специфические интересы игрока , являющийся интерактивным доказательством в
смысле определения из раздела 15.2 и дополнительно
учитывающий эти специфические интересы игрока  . В
случае, если графы . В
случае, если графы  и и  действительно
изоморфны, игрок действительно
изоморфны, игрок  (и даже любой "злоумышленник" (и даже любой "злоумышленник"  с произвольной полиномиально ограниченной вероятностной
стратегией, вступивший в игру с игроком
с произвольной полиномиально ограниченной вероятностной
стратегией, вступивший в игру с игроком  вместо вместо  ) не
получит от игрока ) не
получит от игрока  никакой дополнительной информации в
том смысле, что вся ставшая доступной ему в результате игры
информация (а именно, последовательность результатов
подбрасываний собственной монеты, собственных сообщений и
сообщений игрока никакой дополнительной информации в
том смысле, что вся ставшая доступной ему в результате игры
информация (а именно, последовательность результатов
подбрасываний собственной монеты, собственных сообщений и
сообщений игрока  ) является случайной величиной
(зависящей от подбрасываний монет игроками ) является случайной величиной
(зависящей от подбрасываний монет игроками  и и  ),
которая может быть промоделирована некоторым вероятностным
полиномиальным алгоритмом. Следовательно, игрок ),
которая может быть промоделирована некоторым вероятностным
полиномиальным алгоритмом. Следовательно, игрок  и без
участия игрока и без
участия игрока  мог бы с помощью этого алгоритма
получить эту информацию. Заметим однако, что упомянутый
моделирующий алгоритм сам по себе не пригоден для решения
вопроса, изоморфны ли графы мог бы с помощью этого алгоритма
получить эту информацию. Заметим однако, что упомянутый
моделирующий алгоритм сам по себе не пригоден для решения
вопроса, изоморфны ли графы  и и  (этот аспект
более подробно обсуждается ниже). (этот аспект
более подробно обсуждается ниже).
Такая система доказательства
 называется системой
доказательства с нулевым разглашением. В качестве примера
ниже дается описание соответствующего протокола для языка
ИЗОМОРФИЗМ ГРАФОВ (GRAPH ISOMORPHISM, сокращенно GI),
состоящего из всех пар называется системой
доказательства с нулевым разглашением. В качестве примера
ниже дается описание соответствующего протокола для языка
ИЗОМОРФИЗМ ГРАФОВ (GRAPH ISOMORPHISM, сокращенно GI),
состоящего из всех пар  и и  изоморфных графов
([GMW2]). Предполагаем, что графы изоморфных графов
([GMW2]). Предполагаем, что графы  и и  заданы на одном и том же множестве вершин
заданы на одном и том же множестве вершин  , ,  , и
что , и
что  -- перестановка вершин -- перестановка вершин  , являющаяся
изоморфизмом графов , являющаяся
изоморфизмом графов  и и  , что мы запишем как , что мы запишем как
 . .
Следующий протокол повторяется
последовательно  раз: раз:
 : выбирает случайную перестановку вершин : выбирает случайную перестановку вершин
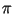 и вычисляет и вычисляет
 ; ;
 : :  ; ;
 : выбирает случайный бит : выбирает случайный бит  ; ;
 : :  ; ;
 : :

 : если : если
 , то
останавливается и выдает отрицательный ответ. Если это
равенство ни разу не было нарушено, то игрок V дает
окончательный положительный ответ. , то
останавливается и выдает отрицательный ответ. Если это
равенство ни разу не было нарушено, то игрок V дает
окончательный положительный ответ.
Изложенный протокол является интерактивным доказательством
для GI. Действительно, игрок  предъявляет граф предъявляет граф  ,
изоморфный ,
изоморфный  , а игрок , а игрок  требует доказать
изоморфность требует доказать
изоморфность  либо либо  , либо , либо  . Если . Если  и и
 изоморфны, то это возможно с вероятностью 1, если
графы неизоморфны, то это возможно лишь с вероятностью изоморфны, то это возможно с вероятностью 1, если
графы неизоморфны, то это возможно лишь с вероятностью
 в каждом вызове протокола и с вероятностью в каждом вызове протокола и с вероятностью  во всех
во всех  вызовах. Этот протокол является протоколом с
нулевым разглашением, так как в случае изоморфных вызовах. Этот протокол является протоколом с
нулевым разглашением, так как в случае изоморфных  и и
 игрок игрок  не получает никакой информации, кроме
изоморфизмов графов не получает никакой информации, кроме
изоморфизмов графов  и и  с какими-то их
случайными перенумерациями, которые он мог бы получить и
самостоятельно, просто-напросто выбирая случайные с какими-то их
случайными перенумерациями, которые он мог бы получить и
самостоятельно, просто-напросто выбирая случайные  и перенумеровывая случайным образом граф
и перенумеровывая случайным образом граф
 . .
Перейдем теперь к формальным определениям, введенным в
работе Гольдвассер, Микали и Ракоффа [GMR1].
Пусть для каждого фиксированного слова
  и и  -- это случайные
величины, значения которых являются двоичными словами. Семейства
случайных величин -- это случайные
величины, значения которых являются двоичными словами. Семейства
случайных величин  и и  называются
статистически неразличимыми (statistically
indistinguishable) на множестве называются
статистически неразличимыми (statistically
indistinguishable) на множестве  , если , если
![$\displaystyle \sum_{s\in \{0,1\}*} \vert\Pr[A(x)=s]-\Pr[B(x)=s]\vert <
\vert x\vert^{-c}
$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img2107.gif) для любой константы
для любой константы  и всех достаточно длинных и всех достаточно длинных  . .
Пусть  для для
 -- это булева схема
(т. е. схема, собранная из элементов -- это булева схема
(т. е. схема, собранная из элементов
 ,
которая при каждой подстановке значений 0 и 1 вместо
входных переменных позволяет получить на выходе значение 0
или 1). Запись ,
которая при каждой подстановке значений 0 и 1 вместо
входных переменных позволяет получить на выходе значение 0
или 1). Запись
 будет означать, что на входном
слове будет означать, что на входном
слове  схема схема  выдает значение 1. Семейство выдает значение 1. Семейство
 называется полиномиально
ограниченным, если для некоторой константы называется полиномиально
ограниченным, если для некоторой константы  и всех достаточно
больших и всех достаточно
больших  количество функциональных элементов в схеме количество функциональных элементов в схеме
 не превосходит не превосходит  . Семейства случайных величин . Семейства случайных величин
 и и  называются вычислительно
неразличимыми
(computationally indistinguishable) на множестве называются вычислительно
неразличимыми
(computationally indistinguishable) на множестве  , если
для произвольного полиномиально ограниченного семейства
схем , если
для произвольного полиномиально ограниченного семейства
схем 
![$\displaystyle \vert\Pr[C_{\vert x\vert}(A(x))=1]-\Pr[C_{\vert x\vert}(B(x))=1]\vert < \vert x\vert^{-c}
$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img2114.gif) для любой константы
для любой константы 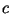 и всех достаточно длинных и всех достаточно длинных  .
Предполагается, что случайные величины .
Предполагается, что случайные величины  и и
 принимают значения, длина которых совпадает с
количеством входных переменных схемы принимают значения, длина которых совпадает с
количеством входных переменных схемы  . .
Легко видеть, что если семейства случайных величин
статистически неразличимы, то они и вычислительно
неразличимы.
Рассмотрим интерактивную систему
 . Внесем в
определение раздела 15.2 следующее дополнение. Пусть . Внесем в
определение раздела 15.2 следующее дополнение. Пусть
 обладает дополнительной входной лентой, на которой
записано дополнительное входное слово обладает дополнительной входной лентой, на которой
записано дополнительное входное слово  (что
соответствует ситуации, когда игрок (что
соответствует ситуации, когда игрок  получил где-то
какую-то дополнительную информацию или запомнил сообщения,
которые он получал в предыдущих вызовах протокола). В
результате выполнения протокола на входе получил где-то
какую-то дополнительную информацию или запомнил сообщения,
которые он получал в предыдущих вызовах протокола). В
результате выполнения протокола на входе  игрок игрок  получает следующую информацию: результаты подбрасываний
своей монеты
получает следующую информацию: результаты подбрасываний
своей монеты  , последовательность , последовательность  своих
сообщений и ответов своих
сообщений и ответов  на них игрока на них игрока  , ,
 . Обозначим последовательность . Обозначим последовательность
 через через
 и будем
рассматривать ее как случайную величину, значение которой
определяется подбрасываниями монет игроками и будем
рассматривать ее как случайную величину, значение которой
определяется подбрасываниями монет игроками  и и  . .
Пусть  -- вероятностная машина Тьюринга, результатом
вычисления которой являются слова (произвольной длины),
зависящие от содержимого ее случайной ленты. Таким
образом, результат вычисления -- вероятностная машина Тьюринга, результатом
вычисления которой являются слова (произвольной длины),
зависящие от содержимого ее случайной ленты. Таким
образом, результат вычисления  на входном слове на входном слове  --
это случайная величина, которую мы будем обозначать через --
это случайная величина, которую мы будем обозначать через
 , зависящая от случайной строки машины , зависящая от случайной строки машины  . Время
работы машины . Время
работы машины  на входе на входе  тоже зависит от полученной
ею случайной строки. Если его математическое ожидание
ограничено полиномом от длины тоже зависит от полученной
ею случайной строки. Если его математическое ожидание
ограничено полиномом от длины  , то говорим, что , то говорим, что  работает за полиномиальное в среднем время.
работает за полиномиальное в среднем время.
Система
 называется интерактивной системой
доказательства с нулевым разглашением для языка называется интерактивной системой
доказательства с нулевым разглашением для языка
 (zero-knowledge interactive proof system, иногда
computationally zero-knowledge, т. е., системой
доказательства с вычислительно нулевым разглашением),
если она является интерактивной системой доказательства для (zero-knowledge interactive proof system, иногда
computationally zero-knowledge, т. е., системой
доказательства с вычислительно нулевым разглашением),
если она является интерактивной системой доказательства для
 , т. е. выполнены условия 1 и 2 из раздела 15.2
(при любом , т. е. выполнены условия 1 и 2 из раздела 15.2
(при любом  ) и, кроме этого, выполняется следующее
условие:
3)
для любой полиномиальной вероятностной машины
Тьюринга ) и, кроме этого, выполняется следующее
условие:
3)
для любой полиномиальной вероятностной машины
Тьюринга  существует вероятностная машина Тьюринга существует вероятностная машина Тьюринга
 , работающая за полиномиальное в среднем время и
такая, что семейства случайных величин , работающая за полиномиальное в среднем время и
такая, что семейства случайных величин
 и и
 вычислительно
неразличимы на множестве вычислительно
неразличимы на множестве
 . .
Система
 называется
интерактивной системой доказательства для называется
интерактивной системой доказательства для  со
статистически нулевым разглашением (statistically zero-knowledge, иногда
almost-perfectly zero-knowledge), если усилить
требование вычислительной неразличимости до статистической
неразличимости. Система со
статистически нулевым разглашением (statistically zero-knowledge, иногда
almost-perfectly zero-knowledge), если усилить
требование вычислительной неразличимости до статистической
неразличимости. Система
 называется интерактивной
системой доказательства для называется интерактивной
системой доказательства для  с абсолютно нулевым
разглашением (perfect zero-knowledge), если потребовать,
чтобы семейства случайных величин с абсолютно нулевым
разглашением (perfect zero-knowledge), если потребовать,
чтобы семейства случайных величин
 и и
 совпадали. совпадали.
Языки, обладающие доказательствами с (абсолютно,
статистически) нулевым разглашением, образуют класс (PZK,
SZK или иногда APZK) ZK. Очевидными являются включения
BPP PZK PZK SZK SZK ZK ZK IP IP
Приведенная выше интерактивная система доказательства для
языка GI является системой с абсолютно нулевым
разглашением.
Замечания
1. Из определения величины
 без всякого ущерба можно исключить сообщения
без всякого ущерба можно исключить сообщения  , ,
 , игрока , игрока  игроку игроку  , так как они однозначно
определяются полиномиальным алгоритмом исходя из
последовательности , так как они однозначно
определяются полиномиальным алгоритмом исходя из
последовательности
 . .
2. Поскольку время работы машины  ограничено
некоторым полиномом, можно считать, что длина
дополнительного входного слова ограничено
некоторым полиномом, можно считать, что длина
дополнительного входного слова  ограничена тем же полиномом
(своим для каждой машины ограничена тем же полиномом
(своим для каждой машины  ). Орен [Ore], который предложил
эту модификацию определения, никаких ограничений на ). Орен [Ore], который предложил
эту модификацию определения, никаких ограничений на  не
накладывал. Выше было объяснено, какой смысл имеет
предоставление игроку не
накладывал. Выше было объяснено, какой смысл имеет
предоставление игроку  дополнительного входного слова дополнительного входного слова  .
Важной мотивацией этого является и то обстоятельство, что без
такой модификации определения интерактивной системы не имеет
места следующий факт (см. [GKr]).
Последовательное выполнение двух протоколов с
нулевым разглашением является протоколом с нулевым
разглашением.
С другой стороны, читателю, обратившемуся к данному
подразделу с целью получения общего представления о понятии
доказательства с нулевым разглашением и не интересующемуся
вопросами композиции протоколов, рекомендуется упростить
данное определение, опустив все упоминания о слове .
Важной мотивацией этого является и то обстоятельство, что без
такой модификации определения интерактивной системы не имеет
места следующий факт (см. [GKr]).
Последовательное выполнение двух протоколов с
нулевым разглашением является протоколом с нулевым
разглашением.
С другой стороны, читателю, обратившемуся к данному
подразделу с целью получения общего представления о понятии
доказательства с нулевым разглашением и не интересующемуся
вопросами композиции протоколов, рекомендуется упростить
данное определение, опустив все упоминания о слове  . .
3. Гольдрайх и Кравчик показали [GKr], что
параллельное выполнение протоколов с нулевым разглашением
не обязательно приводит к протоколам с нулевым разглашением
(сравнить с замечанием 4 раздела 15.2).
4. В определении для любого возможного игрока  мы требуем существования своей моделирующей машины
мы требуем существования своей моделирующей машины
 . Назовем систему с нулевым разглашением
системой с универсальной моделирующей
машиной (black-box
zero-knowledge), если существует вероятностная машина . Назовем систему с нулевым разглашением
системой с универсальной моделирующей
машиной (black-box
zero-knowledge), если существует вероятностная машина  ,
работающая за полиномиальное в среднем время, которая
является моделирующей машиной для любого ,
работающая за полиномиальное в среднем время, которая
является моделирующей машиной для любого  и пользуется
программой и пользуется
программой  как "черным ящиком". Все до сих пор
известные системы с нулевым разглашением являются системами
с универсальными моделирующими машинами. Вопрос о
существовании систем, не обладающих таким свойством,
остается открытым. как "черным ящиком". Все до сих пор
известные системы с нулевым разглашением являются системами
с универсальными моделирующими машинами. Вопрос о
существовании систем, не обладающих таким свойством,
остается открытым.
5. Доказательства с нулевым разглашением тривиальным
образом существуют для всех языков из класса BPP: поскольку
игрок  может сам выяснить принадлежность языку любого данного
слова, диалог с игроком может сам выяснить принадлежность языку любого данного
слова, диалог с игроком  заведомо не дает ему никакой
дополнительной информации. Поэтому, доказательства с нулевым
разглашением являются нетривиальным объектом только при
некоторых теоретико-сложностных предположениях, таких как
P заведомо не дает ему никакой
дополнительной информации. Поэтому, доказательства с нулевым
разглашением являются нетривиальным объектом только при
некоторых теоретико-сложностных предположениях, таких как
P NP. NP.
6. Определение доказательства с нулевым
разглашением, на первый взгляд, может показаться
парадоксальным. В самом деле, корректность протокола
означает, что никакой "злоумышленник" не имеет достойных
внимания шансов обмануть игрока  , и в то же время из
свойства нулевого разглашения следует существование
полиномиальной моделирующей машины, которая достаточно
точно имитирует распределение случайных величин,
возникающих в процессе выполнения протокола. Почему бы
"злоумышленнику" не воспользоваться этой машиной? Для
разрешения этого кажущегося противоречия следует уяснить
следующие два момента. Во-первых, моделирующая машина может
"воспроизвести" только информацию, которую игрок , и в то же время из
свойства нулевого разглашения следует существование
полиномиальной моделирующей машины, которая достаточно
точно имитирует распределение случайных величин,
возникающих в процессе выполнения протокола. Почему бы
"злоумышленнику" не воспользоваться этой машиной? Для
разрешения этого кажущегося противоречия следует уяснить
следующие два момента. Во-первых, моделирующая машина может
"воспроизвести" только информацию, которую игрок  получает в процессе выполнения протокола, но не сам
протокол. Так, для приведенного выше примера моделирующая
машина может строить случайные перенумерации исходных
графов
получает в процессе выполнения протокола, но не сам
протокол. Так, для приведенного выше примера моделирующая
машина может строить случайные перенумерации исходных
графов  и и  , но не может, если ей неизвестен
изоморфизм между этими графами, адекватным образом ответить
на запрос игрока , но не может, если ей неизвестен
изоморфизм между этими графами, адекватным образом ответить
на запрос игрока  , задаваемый случайным битом , задаваемый случайным битом  .
Во-вторых, определение доказательства с нулевым
разглашением описывает поведение моделирующей машины только
на входных словах, принадлежащих данному языку. На
остальных словах эта машина может делать все что угодно.
Поэтому моделирующая машина, с помощью которой
устанавливается свойство нулевого разглашения некоторого
протокола доказательства для данного языка, не может
использоваться для распознавания этого языка (если только
этот язык не принадлежит классу BPP). .
Во-вторых, определение доказательства с нулевым
разглашением описывает поведение моделирующей машины только
на входных словах, принадлежащих данному языку. На
остальных словах эта машина может делать все что угодно.
Поэтому моделирующая машина, с помощью которой
устанавливается свойство нулевого разглашения некоторого
протокола доказательства для данного языка, не может
использоваться для распознавания этого языка (если только
этот язык не принадлежит классу BPP).
Следующая теорема была доказана Гольдрайхом, Микали и
Вигдерсоном [GMW1] (окончательная версия [GMW2]).
Теорема 2.
Если существует односторонняя
перестановка (см. определение ниже), то всякий
язык из класса NP обладает доказательством с нулевым
разглашением, т. е. NP
 ZK. ZK.
Определение.
Взаимно однозначная и сохраняющая длину функция
 , ,
 ,
называется односторонней
перестановкой ((strong
non-uniformly) one-way permutation), если она вычислима за
полиномиальное время и для любого полиномиально
ограниченного семейства булевых схем ,
называется односторонней
перестановкой ((strong
non-uniformly) one-way permutation), если она вычислима за
полиномиальное время и для любого полиномиально
ограниченного семейства булевых схем  (с (с  выходами) для произвольной константы
выходами) для произвольной константы  при достаточно
больших при достаточно
больших 
![$\displaystyle \Pr\left[C_{n}(x)=f^{-1}(x)\right]<1/n^{c},
$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img2129.gif) где вероятность берется по
где вероятность берется по  , равномерно распределенным
на , равномерно распределенным
на
 . .
Обобщение изложенного результата было получено Бен-Ором и
др. [Betal].
Теорема 3.
При условии существования односторонней
перестановки IP ZK, т. е. все, что может быть
доказано интерактивной системой, может быть доказано с
нулевым разглашением. ZK, т. е. все, что может быть
доказано интерактивной системой, может быть доказано с
нулевым разглашением.
Следствие.
При условии существования односторонней перестановки
ZK PSPACE. PSPACE.
Замечание.
Утверждение о том, что теорема 3 верна и при более слабом
предположении о существовании односторонней функции стало
уже частью своеобразного "криптографического фольклора":
оно упоминается в нескольких работах (см., например,
[FKLN]). Однако, нам неизвестно, опубликовано ли
где-нибудь доказательство этого результата.
Естественно возникает вопрос, насколько существенным в
приведенных выше результатах является предположение о
существовании односторонней функции. Островски и
Вигдерсон [OWi] доказали, что если не существует
односторонних функций (в смысле несколько ослабленного
определения), то доказательствами с нулевым разглашением
обладают только языки из класса BPP.





Вперед: Литература
Вверх: 15. Основные понятия теории доказательств с нулевым разглашением
Назад: 15.2 Интерактивные системы доказательства
Содержание
Предметный указатель
|

