




Вперед: 3.4 Аутентификация для интеллектуальных карточек
Вверх: 3.3 Протоколы, основанные на идентификационной информации
Назад: 3.3 Протоколы, основанные на идентификационной информации
Содержание
Предметный указатель
Ниже мы рассматриваем модификацию схемы аутентификации
Фиата и Шамира [FS86], предназначенную для
идентификации интеллектуальных карточек. Для выдачи
интеллектуальных карточек предусмотрен центр доверия.
Прежде чем центр начинает выдавать интеллектуальные
карточки, он выбирает и публикует целое число  , которое
является произведением двух простых чисел , которое
является произведением двух простых чисел  и и  , и
псевдослучайную функцию , и
псевдослучайную функцию  . Простые множители . Простые множители  и и  являются секретными.
являются секретными.
По запросу пользователя центр генерирует строку  , содержащую,
например, имя пользователя, его адрес, идентификационный
номер и т. п. Затем центр выполняет следующие действия:
вычисляет , содержащую,
например, имя пользователя, его адрес, идентификационный
номер и т. п. Затем центр выполняет следующие действия:
вычисляет  значений значений
 для небольших
значений для небольших
значений  , для которых , для которых  является квадратичным
вычетом является квадратичным
вычетом  , и вычисляет наименьший квадратный корень , и вычисляет наименьший квадратный корень
 из из
 . После этого пользователю
выдается интеллектуальная карточка, содержащая . После этого пользователю
выдается интеллектуальная карточка, содержащая  и и  значений значений  с
их индексами. Для простоты изложения в дальнейшем будем предполагать, что
индексы с
их индексами. Для простоты изложения в дальнейшем будем предполагать, что
индексы  принимают значения принимают значения
 . .
Устройство проверки интеллектуальных карточек хранит в своей
памяти число  и функцию и функцию  . Протокол проверки интеллектуальной
карточки состоит в следующем (через A обозначается
доказывающий, т. е. интеллектуальная карточка, а через B
-- проверяющий, т. е. устройство проверки):
1.
A посылает B строку . Протокол проверки интеллектуальной
карточки состоит в следующем (через A обозначается
доказывающий, т. е. интеллектуальная карточка, а через B
-- проверяющий, т. е. устройство проверки):
1.
A посылает B строку  . .
2.
B вычисляет
 , ,
 . .
Следующие шаги выполняются в цикле для
 . .
3.
A выбирает случайное число
 и посылает B значение и посылает B значение
 . .
4.
B выбирает случайный вектор
 и посылает его A. и посылает его A.
5.
A посылает B значение
 . .
6.
B проверяет, что
 .
В результате выполнения протокола B принимает
доказательство A (другими словами, A проходит
аутентификацию), только если проверка п. 6 будет выполнена
во всех .
В результате выполнения протокола B принимает
доказательство A (другими словами, A проходит
аутентификацию), только если проверка п. 6 будет выполнена
во всех 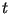 циклах. циклах.
Как уже отмечалось в предыдущем разделе, в работе [FS86] даны
наброски доказательства, что
схема Фиата и Шамира является протоколом доказательства с нулевым
разглашением.
Функция  предполагается общедоступной. Мы описали схему, в
которой предполагается общедоступной. Мы описали схему, в
которой  -- псевдослучайная функция. В оригинале [FS86]
предполагается, что -- псевдослучайная функция. В оригинале [FS86]
предполагается, что  -- случайная функция. В этом
предположении исследована стойкость предложенной схемы.
Вопрос о стойкости в случае использования псевдослучайных
функций, а также проблема практической реализации
генератора псевдослучайных функций не рассматривались. -- случайная функция. В этом
предположении исследована стойкость предложенной схемы.
Вопрос о стойкости в случае использования псевдослучайных
функций, а также проблема практической реализации
генератора псевдослучайных функций не рассматривались.





Вперед: 3.4 Аутентификация для интеллектуальных карточек
Вверх: 3.3 Протоколы, основанные на идентификационной информации
Назад: 3.3 Протоколы, основанные на идентификационной информации
Содержание
Предметный указатель
|

