




Вперед: 4.2.2 Схема Шнорра [Sch]
Вверх: 4.2 Примеры схем электронной подписи
Назад: 4.2 Примеры схем электронной подписи
Содержание
Предметный указатель
Пусть обоим участникам протокола известны некоторое простое
число  , некоторый порождающий , некоторый порождающий  группы группы
 и
некоторая хэш-функция и
некоторая хэш-функция  . Подписывающий выбирает секретный
ключ . Подписывающий выбирает секретный
ключ
 и вычисляет открытый ключ и вычисляет открытый ключ
 . Пространством сообщений в данной схеме является . Пространством сообщений в данной схеме является
 . Для генерации подписи нужно сначала выбрать . Для генерации подписи нужно сначала выбрать
 . Если . Если
 (что проверяется
эффективно), то необходимо выбрать новое (что проверяется
эффективно), то необходимо выбрать новое 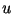 . Если же . Если же
 , то искомой подписью для сообщения , то искомой подписью для сообщения  является пара
является пара 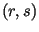 , где , где
 и и
 . Параметр . Параметр 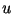 должен быть
секретным и может быть уничтожен после генерации подписи. должен быть
секретным и может быть уничтожен после генерации подписи.
Для проверки подписи 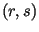 для сообщения для сообщения  необходимо
сначала проверить условия необходимо
сначала проверить условия
 и и
 .
Если хотя бы одно из них ложно, то подпись отвергается. В
противном случае подпись принимается тогда и только тогда,
когда .
Если хотя бы одно из них ложно, то подпись отвергается. В
противном случае подпись принимается тогда и только тогда,
когда
 . .
Вера в стойкость схемы Эль Гамаля основана на
(гипотетической) сложности задачи дискретного
логарифмирования по основанию  . Однако стойкость этой
схемы в предположении сложности дискретного
логарифмирования по основанию . Однако стойкость этой
схемы в предположении сложности дискретного
логарифмирования по основанию  пока не доказана.
Очевидно, что это предположение необходимо для стойкости
схемы Эль Гамаля, так как в противном случае противник
сможет полностью раскрыть схему, вычислив секретный ключ по
известному открытому. пока не доказана.
Очевидно, что это предположение необходимо для стойкости
схемы Эль Гамаля, так как в противном случае противник
сможет полностью раскрыть схему, вычислив секретный ключ по
известному открытому.
Идеи схемы Эль Гамаля послужили основой для создания многих
других схем электронной подписи, включая схемы Шнорра,
DSA, ГОСТ и другие. В этих схемах элемент  иногда порождает не всю группу
иногда порождает не всю группу
 , а некоторую ее
подгруппу простого порядка. , а некоторую ее
подгруппу простого порядка.





Вперед: 4.2.2 Схема Шнорра [Sch]
Вверх: 4.2 Примеры схем электронной подписи
Назад: 4.2 Примеры схем электронной подписи
Содержание
Предметный указатель
| 
