4.2.7 Схемы RSA и Рабина

В данном подразделе мы приводим описание схем подписи, основанных на криптосистемах RSA [RSA] и Рабина [Rab79]. В схеме RSA подписывающий выбирает два различных больших простых числа и , которые играют роль секретного ключа, и публикует соответствующий открытый ключ , где , а -- некоторое число, взаимно простое с ( -- функция Эйлера). Подписью для сообщения является , где (очевидно, что, зная и , можно эффективно вычислить ) и  -- хэш-функция. Проверка подписи для сообщения состоит в проверке сравнения .

Схема Рабина основана на том, что, зная различные простые числа и , можно эффективно извлекать квадратные корни по модулю , тогда как без знания этих простых чисел вышеуказанная задача вычислительно сложна. Секретный ключ в этой схеме тот же, что и в схеме RSA, а открытым ключом является . В качестве пространства сообщений выступает множество всех квадратов элементов группы . Подписью для сообщения является произвольный квадратный корень из 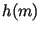по модулю , а проверка подписи для сообщения состоит в проверке сравнения .

Схема RSA достаточно эффективна и широко используется на практике. Вера в стойкость обеих схем основывается на (гипотетической) трудности задачи факторизации целых чисел. Для схемы Рабина доказана, в предположении, что эта гипотеза верна, стойкость против пассивного противника (см. следующий подраздел).