




Вперед: 4.3.3 Схемы, в которых подделка подписи может быть доказана
Вверх: 4.3 Разновидности схем электронной подписи
Назад: 4.3.1 Схемы мультиподписи
Содержание
Предметный указатель
4.3.2 Схемы конфиденциальной (неотвергаемой) подписи
Идея конфиденциальной подписи появилась в работе Шаума и
ван Антверпена [CvA] в 1989 г. В отличие от обычной
электронной подписи, которая может быть проверена в любой
момент времени всяким желающим (поскольку открытый ключ
подписывающего общедоступен, а подпись вместе с сообщением
передается по незащищенным каналам связи, во многих
теоретических работах авторы просто пишут, что подпись
публикуется вместе с сообщением), конфиденциальная подпись
не может быть проверена без участия сгенерировавшего ее
лица. Иными словами, схемы конфиденциальной подписи могут
найти применение в тех случаях, когда сам факт подписания
какого-либо документа определенным лицом не подлежит
огласке. В работах Шаума [Ch90], [Ch91] приводятся
некоторые сценарии использования конфиденциальных подписей
(см. также [CvA], [BCDP]), однако все они
представляются не слишком убедительными. Поэтому, мы
считаем, что практическая значимость этих схем требует
дополнительного анализа, выходящего, однако, за рамки
математических исследований. С математической же точки
зрения схемы конфиденциальной подписи представляют
несомненный интерес как новый криптографический примитив.
В дальнейшем участник протокола, подписавший некоторое
сообщение конфиденциальной подписью, будет обозначаться
через  , а участник, который желает проверить эту подпись
-- через , а участник, который желает проверить эту подпись
-- через  . Для установления подлинности подписи . Для установления подлинности подписи  и и
 выполняют интерактивный протокол, называемый протоколом
верификации, в котором выполняют интерактивный протокол, называемый протоколом
верификации, в котором  доказывает, что подпись была
сгенерирована им. Конфиденциальная подпись предназначается
ограниченному кругу лиц, поэтому естественно считать, что
всякому выполнению протокола верификации предшествует
выполнение протокола идентификации, в котором доказывает, что подпись была
сгенерирована им. Конфиденциальная подпись предназначается
ограниченному кругу лиц, поэтому естественно считать, что
всякому выполнению протокола верификации предшествует
выполнение протокола идентификации, в котором  доказывает свою аутентичность. В случае, если
доказывает свою аутентичность. В случае, если  не
признает своей ту подпись, которую ему предъявил не
признает своей ту подпись, которую ему предъявил  ,
участники выполняют отвергающий протокол, в котором ,
участники выполняют отвергающий протокол, в котором  доказывает, что он не является автором предъявленной
подписи.
доказывает, что он не является автором предъявленной
подписи.
Для обеспечения стойкости схемы конфиденциальной подписи оба
протокола -- и протокол верификации и отвергающий
протокол -- должны быть протоколами доказательства с
нулевым разглашением (см. главу 15), поскольку
необходимо, чтобы в процессе выполнения этих протоколов с
 или с любым злоумышленником, инициировавшим протокол от
имени или с любым злоумышленником, инициировавшим протокол от
имени  , ,  не разглашал никакой информации о своих
секретных ключах. не разглашал никакой информации о своих
секретных ключах.
С практической точки зрения, схемы конфиденциальной подписи
желательно строить на основе того же математического
аппарата, что и схемы обычной подписи. В работе [BCDP]
описана схема конфиденциальной подписи, полученная путем
модификации схемы Эль Гамаля, и предложены наброски
доказательств свойства нулевого разглашения для протокола
верификации и для отвергающего протокола. В данном
подразделе рассматривается схема конфиденциальной подписи,
построенная на основе отечественного стандарта на
электронную подпись (см. подраздел 4.2.5).
Описываемая ниже схема предполагает наличие схемы ЭЦП,
описанной в стандарте (см. также подраздел 4.2.5).
Помимо этого, каждый подписывающий имеет дополнительную
пару (секретный ключ, открытый ключ), причем секретный ключ
 выбирается наудачу из выбирается наудачу из
 , а открытый ключ , а открытый ключ  вычисляется по формуле
вычисляется по формуле
 . .
Тройка  публикуется в общедоступном
сертифицированном справочнике. публикуется в общедоступном
сертифицированном справочнике.
Всюду в дальнейшем предполагается, что подписываемое
сообщение  имеет требуемую для схемы ЭЦП длину. Это
сделано исключительно с целью упрощения изложения (на
практике, разумеется, можно использовать значение
хэш-функции от сообщения). Кроме того, в описаниях протоколов
опущены проверки принадлежности различных величин, получаемых от
другого участника, циклической группе, порождаемой имеет требуемую для схемы ЭЦП длину. Это
сделано исключительно с целью упрощения изложения (на
практике, разумеется, можно использовать значение
хэш-функции от сообщения). Кроме того, в описаниях протоколов
опущены проверки принадлежности различных величин, получаемых от
другого участника, циклической группе, порождаемой  .
Очевидно, что каждый из участников может выполнять все эти
проверки за полиномиальное время. .
Очевидно, что каждый из участников может выполнять все эти
проверки за полиномиальное время.
Подпись сообщения  вычисляется следующим образом.
Выбирается вычисляется следующим образом.
Выбирается
 и вычисляется и вычисляется
 . Затем
вычисляется . Затем
вычисляется
 . Пара . Пара 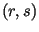 является
подписью для сообщения является
подписью для сообщения  . Подпись считается корректной
тогда и только тогда, когда . Подпись считается корректной
тогда и только тогда, когда
 , где , где
 . Отметим одно
очень существенное отличие этой схемы подписи от стандарта
-- как при вычислении . Отметим одно
очень существенное отличие этой схемы подписи от стандарта
-- как при вычислении  , так и в проверочном соотношении
выполняется приведение только по одному модулю ( , так и в проверочном соотношении
выполняется приведение только по одному модулю ( ). ).
Всюду ниже предполагается, что все вычисления проводятся в
 , поэтому модуль , поэтому модуль  в формулах, как правило, будет
опускаться. в формулах, как правило, будет
опускаться.  обозначает число обозначает число 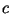 такое, что такое, что
 . Для применения теоретико-сложностных
подходов, все задачи, связанные со схемами подписи, должны
рассматриваться как массовые. Параметром безопасности
служит длина модуля . Для применения теоретико-сложностных
подходов, все задачи, связанные со схемами подписи, должны
рассматриваться как массовые. Параметром безопасности
служит длина модуля  . Принимается следующая гипотеза:
любой полиномиальный алгоритм может по заданным . Принимается следующая гипотеза:
любой полиномиальный алгоритм может по заданным  , ,  и и
 вычислить вычислить  лишь с пренебрежимо малой
вероятностью. лишь с пренебрежимо малой
вероятностью.
Представляется, что проверка конфиденциальной подписи без
участия подписывающего требует вычисления дискретных
логарифмов, и, следовательно, согласно гипотезе,
практически неосуществима. Проверка подписи осуществляется
посредством следующего интерактивного протокола.
Протокол верификации
Проверяющий (абонент  ) вычисляет ) вычисляет
 и просит подписывающего
(абонент и просит подписывающего
(абонент  ) доказать, что пара ) доказать, что пара 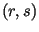 есть его подпись
под сообщением есть его подпись
под сообщением  . Эта задача эквивалентна доказательству,
что дискретный логарифм . Эта задача эквивалентна доказательству,
что дискретный логарифм  по основанию по основанию  равен (по
модулю равен (по
модулю  ) дискретному логарифму ) дискретному логарифму  по основанию по основанию  ,
т. е. ,
т. е.
 . Для этого:
1.
Абонент . Для этого:
1.
Абонент  выбирает выбирает
 , вычисляет , вычисляет
 и посылает и посылает  абоненту абоненту  . .
2.
Абонент  выбирает выбирает
 , вычисляет , вычисляет
 , ,
 и посылает и посылает
 и и  абоненту абоненту  . .
3.
Абонент  высылает параметры высылает параметры  и и  . .
4.
Если
 , то абонент , то абонент  посылает посылает
 параметр параметр 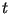 ; в противном случае -- останавливается. ; в противном случае -- останавливается.
5.
Абонент  проверяет выполнение равенств проверяет выполнение равенств
 и и
 .
Если проверка завершена успешно, то подпись принимается как
корректная. .
Если проверка завершена успешно, то подпись принимается как
корректная.
Теорема 1.
Протокол верификации является протоколом
доказательства с абсолютно нулевым разглашением.
В отвергающем протоколе  доказывает доказывает  , что , что
 . .
Отвергающий протокол
Следующие шаги выполняются в цикле  раз.
1. раз.
1.
 выбирает выбирает
 , ,  , ,
 . Вычисляет . Вычисляет  , ,  , если , если
 и и  , ,
 , если , если  . Посылает . Посылает
 значения значения  , ,  , ,  . .
2.
 проверяет соотношение проверяет соотношение  . Если оно
выполняется, то . Если оно
выполняется, то  , иначе , иначе  . Выбирает . Выбирает
 , вычисляет , вычисляет
 и посылает и посылает  значение
значение 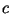 . .
3.
 посылает посылает  значение значение  . .
4.
 проверяет, что выполняется одно из соотношений проверяет, что выполняется одно из соотношений
 или или
 . Если да, то
посылает . Если да, то
посылает  значение значение  . Иначе останавливается. . Иначе останавливается.
5.
 проверяет, что проверяет, что
 . .
Если во всех  циклах проверка в п. 5 выполнена, то циклах проверка в п. 5 выполнена, то  принимает доказательство.
принимает доказательство.
Теорема 2.
Отвергающий
протокол является протоколом доказательства с абсолютно
нулевым разглашением.





Вперед: 4.3.3 Схемы, в которых подделка подписи может быть доказана
Вверх: 4.3 Разновидности схем электронной подписи
Назад: 4.3.1 Схемы мультиподписи
Содержание
Предметный указатель
|

