




Вперед: 4.3.4 Групповая подпись
Вверх: 4.3 Разновидности схем электронной подписи
Назад: 4.3.2 Схемы конфиденциальной (неотвергаемой) подписи
Содержание
Предметный указатель
Пусть  обозначает параметр
безопасности, обозначает параметр
безопасности,  и и  -- соответственно секретный и
открытый ключи подписывающего, а -- соответственно секретный и
открытый ключи подписывающего, а  и и  -- алгоритмы
генерации и проверки подписей соответственно (см. подраздел 4.6.1). Предположим, что некоторая
одноразовая схема электронной подписи удовлетворяет
следующим условиям (см. [HP]):
1.
Для любых -- алгоритмы
генерации и проверки подписей соответственно (см. подраздел 4.6.1). Предположим, что некоторая
одноразовая схема электронной подписи удовлетворяет
следующим условиям (см. [HP]):
1.
Для любых  , ,  и сообщения и сообщения  мощность
множества мощность
множества  всех секретных ключей всех секретных ключей  , соответствующих , соответствующих
 и таких, что и таких, что
 , экспоненциальна от , экспоненциальна от  .
Кроме того, для любого сообщения .
Кроме того, для любого сообщения  при при

 пренебрежимо мала. пренебрежимо мала.
2.
Существует полиномиальный алгоритм, вычисляющий по
 , ,  , сообщению , сообщению  и допустимой подписи и допустимой подписи
 для сообщения
для сообщения  некоторую информацию, доказывающую, что
подпись некоторую информацию, доказывающую, что
подпись  поддельная. поддельная.
3.
Никакой полиномиально ограниченный подписывающий не
может вычислить с не пренебрежимо малой
вероятностью допустимую подпись для данного сообщения и
информацию, доказывающую ее поддельность.
Неформально эти условия означают следующее. Если противник,
имея открытый ключ  законного подписывающего и его
подпись законного подписывающего и его
подпись  для некоторого сообщения для некоторого сообщения  , каким-либо
образом подделал подпись для другого сообщения , каким-либо
образом подделал подпись для другого сообщения  (например, нашел некоторый секретный ключ
(например, нашел некоторый секретный ключ  ,
соответствующий ,
соответствующий  , и вычислил , и вычислил  ), то ввиду
условия 1 эта поддельная подпись ), то ввиду
условия 1 эта поддельная подпись  с большой
вероятностью будет отличаться от подписи с большой
вероятностью будет отличаться от подписи  законного подписывающего. В этом случае законный
подписывающий может доказать поддельность
законного подписывающего. В этом случае законный
подписывающий может доказать поддельность  ,
воспользовавшись алгоритмом из условия 2. В поддельности ,
воспользовавшись алгоритмом из условия 2. В поддельности
 могут убедиться также проверяющий или арбитр, получив
от подписывающего его секретный ключ. Таким образом,
условия 1 и 2 обеспечивают безопасность подписывающего,
защищая его от действий противника (даже обладающего
неограниченными вычислительными возможностями). Условие
же 3 обеспечивает безопасность проверяющего, защищая его от
действий нечестного подписывающего, который ввиду этого
условия не может отказаться от своей подписи, сославшись на
ее поддельность. Отметим, что безопасность подписывающего
(доказуемость подделки) носит безусловный
(теоретико-информационный) характер, а безопасность
проверяющего -- теоретико-сложностной. могут убедиться также проверяющий или арбитр, получив
от подписывающего его секретный ключ. Таким образом,
условия 1 и 2 обеспечивают безопасность подписывающего,
защищая его от действий противника (даже обладающего
неограниченными вычислительными возможностями). Условие
же 3 обеспечивает безопасность проверяющего, защищая его от
действий нечестного подписывающего, который ввиду этого
условия не может отказаться от своей подписи, сославшись на
ее поддельность. Отметим, что безопасность подписывающего
(доказуемость подделки) носит безусловный
(теоретико-информационный) характер, а безопасность
проверяющего -- теоретико-сложностной.
Схема электронной подписи, удовлетворяющая условиям 1-3,
названа в работе ван Хейста и Педерсена [HP]
схемой, останавливаемой при сбоях (fail-stop signature scheme).
Название связано с тем, что подписывающий, обнаружив и
доказав подделку подписи, может остановить использование
схемы. Однако первая такая схема была предложена Вайднером
и Пфитцман [WP], в более поздней работе которых вместе
с Блоймером [BPW] она была названа схемой, в
которой подделка подписи может быть доказана (scheme where
forgery can be proved). Нам представляется, что второе
название более точно отражает сущность этих схем.
Важность свойства доказуемости подделки вытекает из
следующих соображений. В настоящее время стойкость всех
схем электронной подписи (в смысле
подраздела. 4.6.1) основана на некоторых
недоказанных предположениях (сложность задач факторизации,
дискретного логарифмирования и т. п.). Поэтому не
исключено, что в будущем будут найдены эффективные методы
решения подобных задач. Схема электронной подписи,
обладающая свойством доказуемости подделки, позволяет
защищаться даже от противника, который вооружен таким
методом.
Как уже отмечалось, первая схема электронной подписи, в
которой подделка может быть доказана, предложена Вайднером
и Пфитцман в [WP]. А именно, в этой работе было
замечено, что схема Лампорта (см. п. 4.6.2.2)
является таковой, если в ней функция  удовлетворяет
следующим условиям:
1)
для некоторой (достаточно большой) константы удовлетворяет
следующим условиям:
1)
для некоторой (достаточно большой) константы 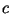 и
для любого и
для любого   имеет не менее имеет не менее  прообразов; прообразов;
2)
нахождение коллизий функции  (т. е. таких пар (т. е. таких пар
 , что , что
 и и
 ) является вычислительно трудной задачей для
подписывающего.
Действительно, в этом случае легко проверить истинность
условий 1-3 (в качестве информации, доказывающей
поддельность подписи, выступает коллизия функции ) является вычислительно трудной задачей для
подписывающего.
Действительно, в этом случае легко проверить истинность
условий 1-3 (в качестве информации, доказывающей
поддельность подписи, выступает коллизия функции  ).
Авторы [WP] при некотором криптографическом
предположении строят односторонние функции, удовлетворяющие
условиям 1) и 2). Дальнейшее развитие этого подхода
предлагается в работе Блоймера, Пфитцман и
Вайднера [BPW]. ).
Авторы [WP] при некотором криптографическом
предположении строят односторонние функции, удовлетворяющие
условиям 1) и 2). Дальнейшее развитие этого подхода
предлагается в работе Блоймера, Пфитцман и
Вайднера [BPW].
Однако в вышеописанной схеме сообщения подписываются
побитово, поэтому длина подписи очень велика. В работе
ван Хейста и Педерсена [HP] предлагается более
эффективная схема электронной подписи, в которой подделка
может быть доказана. Приведем ее описание. Пусть  и и  -- большие простые числа такие, что
-- большие простые числа такие, что  делит делит 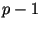 , а , а  и
и  -- элементы порядка -- элементы порядка  в группе в группе
 .
Предполагается, что .
Предполагается, что  , ,  , ,  и и  известны как
подписывающему, так и проверяющему, но ни тому, ни другому
не известен дискретный логарифм известны как
подписывающему, так и проверяющему, но ни тому, ни другому
не известен дискретный логарифм  по основанию по основанию  (т. е.
такое (т. е.
такое
 , что , что
 ). Секретный ключ
подписывающего имеет вид ). Секретный ключ
подписывающего имеет вид
 а соответствующий открытый ключ вычисляется по формуле
а соответствующий открытый ключ вычисляется по формуле
 Чтобы подписать сообщение
Чтобы подписать сообщение
 , подписывающий
вычисляет , подписывающий
вычисляет
 Подпись
Подпись
 признается
допустимой, если и только если признается
допустимой, если и только если
 Далее авторы [HP] доказывают, что при данных
Далее авторы [HP] доказывают, что при данных  , ,  , ,
 а)
существует в точности
а)
существует в точности  секретных ключей секретных ключей
 , соответствующих , соответствующих  и таких, что и таких, что
 ; ;
б)
для любого сообщения  и любой
допустимой подписи и любой
допустимой подписи  для для  существует единственный
секретный ключ существует единственный
секретный ключ  , удовлетворяющий условию п. а) и такой,
что , удовлетворяющий условию п. а) и такой,
что
 ; ;
в)
если известны  , ,  и некоторая допустимая
подпись и некоторая допустимая
подпись
 для сообщения для сообщения  , то можно
эффективно вычислить дискретный логарифм , то можно
эффективно вычислить дискретный логарифм  по основанию по основанию
 .
Из этих утверждений легко вытекает истинность условий 1 и 2
(если .
Из этих утверждений легко вытекает истинность условий 1 и 2
(если  и и  -- случайный элемент,
удовлетворяющий условию п. а), то -- случайный элемент,
удовлетворяющий условию п. а), то
 ввиду а) и б), а в качестве
информации, доказывающей поддельность подписи, выступает
дискретный логарифм ввиду а) и б), а в качестве
информации, доказывающей поддельность подписи, выступает
дискретный логарифм  по основанию по основанию  ). Условие же 3
будет истинным, если дискретные логарифмы в (единственной)
подгруппе порядка ). Условие же 3
будет истинным, если дискретные логарифмы в (единственной)
подгруппе порядка  группы группы
 вычисляются сложно. вычисляются сложно.
Вышеописанная схема является одноразовой, так как если
известны  и и  при при  , то можно
вычислить , то можно
вычислить  . В работе [HP] предложены также
некоторые модификации этой схемы, позволяющие подписывать
несколько сообщений без смены ключей. Кроме того, в этой
работе приведена схема конфиденциальной (undeniable --
см. подраздел 4.3.2) подписи, безусловно стойкая
для подписывающего и позволяющая ему конвертировать
конфиденциальные подписи в подписи, подделка которых может
быть доказана. За подробностями мы отсылаем читателя к
оригинальной работе [HP]. . В работе [HP] предложены также
некоторые модификации этой схемы, позволяющие подписывать
несколько сообщений без смены ключей. Кроме того, в этой
работе приведена схема конфиденциальной (undeniable --
см. подраздел 4.3.2) подписи, безусловно стойкая
для подписывающего и позволяющая ему конвертировать
конфиденциальные подписи в подписи, подделка которых может
быть доказана. За подробностями мы отсылаем читателя к
оригинальной работе [HP].





Вперед: 4.3.4 Групповая подпись
Вверх: 4.3 Разновидности схем электронной подписи
Назад: 4.3.2 Схемы конфиденциальной (неотвергаемой) подписи
Содержание
Предметный указатель
|

