




Вперед: 4.6.2 Математические аспекты разработки схем электронной подписи
Вверх: 4.6 Теоретические результаты
Назад: 4.6 Теоретические результаты
Содержание
Предметный указатель
4.6.1 Основные понятия
Приведем необходимые определения. Согласно работам
Гольдвассер, Микали, Ривеста [GMRiv] и Беллара, Микали
[BeMi] протокол (схема)
электронной подписи
состоит из следующих компонентов:
1. Параметр безопасности (security parameter)  . В качестве . В качестве
 может выступать длина подписи, длина подписываемых сообщений
и т. п. Однако для каждой данной схемы род параметра
безопасности должен быть фиксирован. может выступать длина подписи, длина подписываемых сообщений
и т. п. Однако для каждой данной схемы род параметра
безопасности должен быть фиксирован.
2. Пространство сообщений (message space)  . Обычно
предполагается, что . Обычно
предполагается, что
 , где , где  полиномиально от
полиномиально от  . .
3. Граница числа подписей (signature bound)  --
число (зависящее, вообще говоря, от параметра
безопасности), ограничивающее общее количество подписей,
которые могут быть получены в данной схеме без замены
секретной информации. --
число (зависящее, вообще говоря, от параметра
безопасности), ограничивающее общее количество подписей,
которые могут быть получены в данной схеме без замены
секретной информации.
4. Алгоритм генерации ключей (key generation algorithm)
-- полиномиальный (от  ) вероятностный алгоритм ) вероятностный алгоритм  ,
генерирующий по данному параметру безопасности ,
генерирующий по данному параметру безопасности  пару пару
 , где , где  -- секретный ключ подписывающего, а -- секретный ключ подписывающего, а  -- соответствующий открытый ключ. Если
-- соответствующий открытый ключ. Если  -- это длина
подписи или подписываемых сообщений, то на вход алгоритма -- это длина
подписи или подписываемых сообщений, то на вход алгоритма
 должна подаваться строка должна подаваться строка  . .
5. Алгоритм генерации подписей (signature algorithm) --
полиномиальный (от  ) вероятностный алгоритм ) вероятностный алгоритм  ,
генерирующий по данным сообщению ,
генерирующий по данным сообщению  и секретному
ключу и секретному
ключу  (кроме этих, возможны и другие входные параметры)
подпись (кроме этих, возможны и другие входные параметры)
подпись  для сообщения для сообщения  . .
6. Алгоритм проверки подписей (verification algorithm)
-- полиномиальный вероятностный алгоритм  , генерирующий
по данным сообщению , генерирующий
по данным сообщению  , открытому ключу , открытому ключу  и
возможной подписи и
возможной подписи  либо 1 (в этом случае говорят, что
подпись либо 1 (в этом случае говорят, что
подпись  для сообщения для сообщения  принята) либо 0
(подпись отвергнута). принята) либо 0
(подпись отвергнута).
Все вышеуказанные параметры и алгоритмы, кроме секретного
ключа, предполагаются общедоступными. Отметим, что алгоритм
 обязан быть вероятностным, так как в противном случае
противник может получить секретный ключ обязан быть вероятностным, так как в противном случае
противник может получить секретный ключ  . Алгоритмы . Алгоритмы  и и
 , напротив, могут быть детерминированными. , напротив, могут быть детерминированными.
Говорят, что  -- допустимая подпись для сообщения -- допустимая подпись для сообщения  , если она принимается алгоритмом , если она принимается алгоритмом
 с не пренебрежимо малой вероятностью, т. е. с не пренебрежимо малой вероятностью, т. е.
 для некоторой
константы для некоторой
константы  и для всех достаточно больших и для всех достаточно больших  .
Разумеется, необходимо, чтобы подпись .
Разумеется, необходимо, чтобы подпись  была
допустимой для сообщения была
допустимой для сообщения  или даже принималась с
вероятностью или даже принималась с
вероятностью 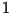 , но, вообще говоря, для этого сообщения
могут существовать и другие допустимые подписи.
Подделкой подписи для сообщения , но, вообще говоря, для этого сообщения
могут существовать и другие допустимые подписи.
Подделкой подписи для сообщения
 называется нахождение противником, не имеющим
секретного ключа подписывающего, допустимой подписи для
этого сообщения. называется нахождение противником, не имеющим
секретного ключа подписывающего, допустимой подписи для
этого сообщения.
Таким образом, в протоколе электронной подписи
подписывающий участник,
(отправитель, sender) сначала вычисляет
 и
посылает и
посылает  проверяющему, участнику
(получателю, recipient'у), сохраняя проверяющему, участнику
(получателю, recipient'у), сохраняя  в секрете. Чтобы
подписать сообщение в секрете. Чтобы
подписать сообщение  , подписывающий вычисляет , подписывающий вычисляет
 и посылает и посылает  и и  проверяющему, который после
этого вычисляет проверяющему, который после
этого вычисляет  и в зависимости от результата
этого вычисления принимает или отвергает подпись и в зависимости от результата
этого вычисления принимает или отвергает подпись  для
сообщения для
сообщения  . Отметим, что в большинстве протоколов
электронной подписи информация пересылается только от
подписывающего участника к проверяющему (протоколы не
являются интерактивным). . Отметим, что в большинстве протоколов
электронной подписи информация пересылается только от
подписывающего участника к проверяющему (протоколы не
являются интерактивным).
Стойкость протокола электронной подписи определяется тем,
какие действия по "взламыванию" протокола, называемые
угрозами, противник может осуществить,
проведя некоторые действия по получению информации о
протоколе, называемые атаками.
Предполагается, что к концу любой атаки противник имеет
открытый ключ  . .
Определение.
Схема подписи называется нестойкой против некоторой угрозы (за исключением
универсальной подделки -- см. ниже) на основе некоторой
атаки, если существует полиномиальный от  вероятностный
алгоритм (противник), осуществляющий при
возможности проведения данной атаки данную угрозу с
вероятностью не менее вероятностный
алгоритм (противник), осуществляющий при
возможности проведения данной атаки данную угрозу с
вероятностью не менее  (где (где 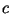 -- некоторая
положительная константа) для бесконечного множества
параметров -- некоторая
положительная константа) для бесконечного множества
параметров  . Вероятность берется по совместному
распределению входных данных и случайных битов,
используемых алгоритмом. Схема, не являющаяся нестойкой,
называется стойкой. . Вероятность берется по совместному
распределению входных данных и случайных битов,
используемых алгоритмом. Схема, не являющаяся нестойкой,
называется стойкой.
В работе [GMRiv] описаны следующие типы угроз и атак
(мы приводим их в порядке возрастания силы):
Типы угроз
1. Экзистенциальная подделка (existential forgery) --
подделка подписи для какого-нибудь (возможно,
бессмысленного) сообщения, отличного от сообщений, которые
противник получает или выбирает при осуществлении атак. При
этом противник не контролирует выбор этого сообщения.
2. Селективная подделка (selective forgery) -- подделка
подписи для сообщения, выбранного противником априори.
3. Универсальная подделка (universal forgery) --
нахождение эффективного алгоритма генерации подписи,
функционально эквивалентного
 . .
4. Полное раскрытие (a total break) -- вычисление
некоторого секретного ключа, соответствующего открытому
ключу  (что дает возможность генерировать подписи для
любых сообщений). Отметим, что, вообще говоря, таких ключей
может быть несколько. (что дает возможность генерировать подписи для
любых сообщений). Отметим, что, вообще говоря, таких ключей
может быть несколько.
Типы атак
1. Атака с открытым ключом (key-only attack). Противник
получает только открытый ключ  . .
2. Атака с известными сообщениями (known-message
attack). Противник получает полиномиальное от  количество пар вида
количество пар вида  , где , где  -- некоторое
сообщение, а -- некоторое
сообщение, а  -- допустимая подпись для -- допустимая подпись для  . При этом
противник никак не влияет на выбор сообщений . При этом
противник никак не влияет на выбор сообщений  из этих
пар. из этих
пар.
3. Простая атака с выбором сообщений (generic
chosen-message attack). Противник выбирает набор сообщений
 , где , где  ограничено
некоторым полиномом от ограничено
некоторым полиномом от  , и получает набор , и получает набор
 , где , где  -- допустимая подпись для -- допустимая подпись для
 . Предполагается, что сообщения . Предполагается, что сообщения  выбираются
независимо от открытого ключа выбираются
независимо от открытого ключа  . Таким образом, эта атака
не направлена против конкретного подписывающего. . Таким образом, эта атака
не направлена против конкретного подписывающего.
4. Направленная атака с выбором сообщений (directed
chosen-message attack). Противник
получает открытый ключ  , выбирает набор сообщений , выбирает набор сообщений
 , где , где  ограничено
некоторым полиномом от ограничено
некоторым полиномом от  , и
получает набор , и
получает набор
 , где , где  --
допустимая подпись для --
допустимая подпись для  . В отличие от предыдущей
эта атака направлена против конкретного подписывающего
(которому соответствует открытый ключ . В отличие от предыдущей
эта атака направлена против конкретного подписывающего
(которому соответствует открытый ключ  ). ).
5. Адаптивная атака с выбором сообщений (adaptive
chosen-message attack). Противник получает открытый ключ
 , выбирает сообщение , выбирает сообщение 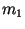 и получает допустимую подпись и получает допустимую подпись
 для для 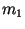 , затем выбирает сообщение , затем выбирает сообщение  и получает
допустимую подпись и получает
допустимую подпись  для для  и т. д.; возможно
полиномиальное от и т. д.; возможно
полиномиальное от  число циклов выбора сообщения и
получения допустимой подписи для него. Другими словами,
противник может обращаться к оракулу, дающему допустимые
подписи для сообщений. число циклов выбора сообщения и
получения допустимой подписи для него. Другими словами,
противник может обращаться к оракулу, дающему допустимые
подписи для сообщений.





Вперед: 4.6.2 Математические аспекты разработки схем электронной подписи
Вверх: 4.6 Теоретические результаты
Назад: 4.6 Теоретические результаты
Содержание
Предметный указатель
|

