




Вперед: 5.5 Теоретические аспекты
Вверх: 5. Хэш-функции
Назад: 5.3 Вопросы эффективности
Содержание
Предметный указатель
5.4 Методы криптоанализа хэш-функций
Ввиду большого разнообразия способов построения
хэш-функций, универсальных методов поиска коллизий не
существует. Для тех хэш-функций, которые мы в
разделе 5.2 условно отнесли ко второй группе,
единственная возможность нахождения эффективных алгоритмов
поиска коллизий состоит в анализе соответствующих
математических задач. Так, используя некоторые свойства
задачи РЮКЗАК, Камион и Патарэн [CP] разработали
алгоритм, который для хэш-функции Дамгорда [D] находит
 такое, что такое, что  для произвольного, но
фиксированного значения для произвольного, но
фиксированного значения  , за приблизительно , за приблизительно
 операций и используя 128 Гбайтов памяти. Патарэн
[Pat] модифицировал этот алгоритм для поиска коллизий.
Модифицированный алгоритм требует порядка операций и используя 128 Гбайтов памяти. Патарэн
[Pat] модифицировал этот алгоритм для поиска коллизий.
Модифицированный алгоритм требует порядка  операций
и порядка 512 Мбайтов памяти. Эти работы интересно сравнить
с приведенным в разделе 5.5 результатом
Импальяццо и Наора о доказуемой стойкости семейства
хэш-функций, основанного на модульной задаче РЮКЗАК
(теорема 4). операций
и порядка 512 Мбайтов памяти. Эти работы интересно сравнить
с приведенным в разделе 5.5 результатом
Импальяццо и Наора о доказуемой стойкости семейства
хэш-функций, основанного на модульной задаче РЮКЗАК
(теорема 4).
Для хэш-функций, у которых длина хэш-значения невелика,
универсальным методом поиска коллизий является метод,
основанный на так называемом "парадоксе дня
рождения" (birthday paradox). Этот метод хорошо известен
в криптографии и был описан еще в 1979 г. Ювалом [Yuv]. Пусть длина хэш-значения равна  битам. Атака состоит в генерации двух псевдослучайных
наборов сообщений по
битам. Атака состоит в генерации двух псевдослучайных
наборов сообщений по  сообщений каждое. Тогда,
согласно парадоксу дня рождения, вероятность того, что в
этих наборах найдется пара сообщений, имеющих одинаковые
хэш-значения, больше сообщений каждое. Тогда,
согласно парадоксу дня рождения, вероятность того, что в
этих наборах найдется пара сообщений, имеющих одинаковые
хэш-значения, больше  . Метод требует большого объема
памяти для хранения генерируемых наборов, а также
эффективных методов сортировки. . Метод требует большого объема
памяти для хранения генерируемых наборов, а также
эффективных методов сортировки.
По существу, на той же идее основаны и алгоритмы поиска
коллизий для функций шифрования блочных шифраторов. Пусть
 -- такая функция, где -- такая функция, где  -- блок сообщения, а -- блок сообщения, а
 -- ключ. Коллизией для -- ключ. Коллизией для  называется тройка называется тройка
 такая, что такая, что
 . Если
зафиксировать некоторое значение . Если
зафиксировать некоторое значение  , то , то  можно
рассматривать как функцию от одного аргумента. Далее
случайно выбирается некоторое начальное значение ключа можно
рассматривать как функцию от одного аргумента. Далее
случайно выбирается некоторое начальное значение ключа  и вычисляется последовательность
и вычисляется последовательность
 , ,
 , ,
 , ,  . Как только будут
найдены константы . Как только будут
найдены константы  и и 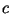 такие, что такие, что
 , но , но
 ,
алгоритм завершает работу, поскольку ,
алгоритм завершает работу, поскольку
 и и
 образуют искомую коллизию. Для шифраторов
типа DES, где длина ключа меньше длины блока, на каждом
шаге необходимо применить некоторую "проецирующую" функцию (выбор которой может существенно повлиять на
эффективность поиска). Проблемой, опять-таки, является
большой объем памяти, требуемой для хранения промежуточных
значений. Кискате и Делесэй [QD1], [QD2]
предлагают запоминать лишь некоторые "выделенные" значения (на практике, они хранили те значения, в которых
фиксированные 20 битов равны 0). Это приводит к некоторому
замедлению работы алгоритма, поскольку при обнаружении
совпадающих выделенных значений необходимо вернуться к
предыдущим таким значениям и повторить часть вычислений,
запоминая уже все промежуточные результаты. Однако
значительная экономия памяти делает этот метод применимым
на практике. Так, в работах Кискате и Делесэя [QD1],
[QD2] сообщается о результатах вычислительного
эксперимента по поиску коллизий для DES. Было обнаружено
26 коллизий для одного и того же сообщения. Это позволяет
строить коллизии, например, для хэш-функции Дэвиса --
Мейера, описанной в разделе 5.2. В самом деле,
пусть образуют искомую коллизию. Для шифраторов
типа DES, где длина ключа меньше длины блока, на каждом
шаге необходимо применить некоторую "проецирующую" функцию (выбор которой может существенно повлиять на
эффективность поиска). Проблемой, опять-таки, является
большой объем памяти, требуемой для хранения промежуточных
значений. Кискате и Делесэй [QD1], [QD2]
предлагают запоминать лишь некоторые "выделенные" значения (на практике, они хранили те значения, в которых
фиксированные 20 битов равны 0). Это приводит к некоторому
замедлению работы алгоритма, поскольку при обнаружении
совпадающих выделенных значений необходимо вернуться к
предыдущим таким значениям и повторить часть вычислений,
запоминая уже все промежуточные результаты. Однако
значительная экономия памяти делает этот метод применимым
на практике. Так, в работах Кискате и Делесэя [QD1],
[QD2] сообщается о результатах вычислительного
эксперимента по поиску коллизий для DES. Было обнаружено
26 коллизий для одного и того же сообщения. Это позволяет
строить коллизии, например, для хэш-функции Дэвиса --
Мейера, описанной в разделе 5.2. В самом деле,
пусть  и и  -- два блока таких, что -- два блока таких, что
 . Тогда
сообщения . Тогда
сообщения
 и и
 имеют одинаковые хэш-значения при любых имеют одинаковые хэш-значения при любых
 . .
Аналогичным методом в работе [QD2] была найдена
коллизия  и и  для фиксированных значений для фиксированных значений
 и и  следующего вида: следующего вида:
 Ее также можно использовать для построения коллизий для той
же хэш-функции. Пусть
Ее также можно использовать для построения коллизий для той
же хэш-функции. Пусть  и и
 .
Тогда сообщения .
Тогда сообщения
 и и
 имеют одинаковые
хэш-значения при любых имеют одинаковые
хэш-значения при любых
 . .
Как уже отмечалось выше, при построении хэш-функций "с
нуля" применяются те же методы и конструкции, что и при
разработке блочных шифраторов. Поэтому к ним применимы и
все методы криптоанализа шифраторов. Например, Бихам и
Шамир в своей известной работе [BS], посвященной
дифференциальному криптоанализу, описывают в числе прочих и
успешную атаку с помощью этого метода на хэш-функцию Snefru
[Me].
Помимо методов поиска коллизий, криптоанализ хэш-функций
включает в себя также широкий спектр методов анализа
слабостей алгоритмов хэширования. Хотя эти слабости не
приводят к прямым атакам на хэш-функции, они влияют на
оценку стойкости последних.
В работе Миягучи, Охты и Иваты [MOI] излагаются
атаки на некоторые хэш-функции, построенные с помощью
блочных шифраторов. Часть этих атак осуществима только при
некоторых дополнительных условиях, например, в
предположении, что противник может изменять начальные
значения.





Вперед: 5.5 Теоретические аспекты
Вверх: 5. Хэш-функции
Назад: 5.3 Вопросы эффективности
Содержание
Предметный указатель
|

