Пусть на глубине 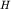 параллельно оси y
расположен бесконечно длинный цилиндр с магнитным моментом единицы
длины, равным параллельно оси y
расположен бесконечно длинный цилиндр с магнитным моментом единицы
длины, равным  , где , где 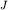 - интенсивность
намагничивания, постоянная для всего цилиндра и направленная вертикально, - интенсивность
намагничивания, постоянная для всего цилиндра и направленная вертикально,
 - поперечное сечение цилиндра (рис. 2.7). Требуется
определить напряженность поля вдоль оси - поперечное сечение цилиндра (рис. 2.7). Требуется
определить напряженность поля вдоль оси  . Поле такого цилиндра
можно считать эквивалентным полю бесконечного числа вертикальных
магнитных диполей, центры которых расположены по оси цилиндра. . Поле такого цилиндра
можно считать эквивалентным полю бесконечного числа вертикальных
магнитных диполей, центры которых расположены по оси цилиндра.
 | | Рис. 2.7. Магнитное поле горизонтального цилиндра бесконечного простирания |
Потенциал в точке  от элементарного диполя определяется согласно уравнению (2.5):
от элементарного диполя определяется согласно уравнению (2.5):
где 
Потенциал всего цилиндра равен
потенциалу от системы диполей, расположенных вдоль оси бесконечного
цилиндра, или интегралу по объему цилиндра от выражения для потенциала
элементарного диполя:
Так как  , то , то  и и
 | (2.14) |
Легко видеть, что при  будет максимум будет максимум  а при а при  При
При  значения значения  будут
отрицательны, при будут
отрицательны, при  - положительны. - положительны.
В плане над горизонтальным цилиндром будут вытянутые
аномалии двух знаков.
При решении обратной задачи глубину залегания цилиндра
можно определить по формулам:  , где , где  и и  - абсциссы точек, в которых - абсциссы точек, в которых
 и и  . Зная . Зная  , можно найти погонную массу цилиндра , можно найти погонную массу цилиндра
 Заменив Заменив  , получим , получим  . Зная . Зная  и и  можно рассчитывать
площадь сечения цилиндра. можно рассчитывать
площадь сечения цилиндра.
Пользуясь формулой
(2.6), можно решать прямые задачи для тел других форм и невертикальной
намагниченности. Практически эти расчеты реализуются с помощью ЭВМ.
Обратные задачи можно решать методом сравнения наблюденных графиков
или карт аномальных магнитных полей с теоретически рассчитанными
для меняющихся геометрических параметров и магнитных свойств. Получив
наименьшие расхождения между ними, теоретические параметры совпавшей
модели переносятся на реальные объекты. Они играют роль одного из
эквивалентных решений (см. 6.1).
Измерения магнитного поля Земли и его вариаций проводят как
на стационарных пунктах - магнитных oбсерваториях, которых насчитывается
на Земле около 150, так и при магниторазведочных работах. Абсолютные
определения полного вектора напряженности геомагнитного поля сводятся
к измерению, как правило, трех его элементов (например,  ). Для этого применяют сложные трехкомпонентные
магнитные приборы, которые называются магнитными теодолитами и вариационными
станциями. ). Для этого применяют сложные трехкомпонентные
магнитные приборы, которые называются магнитными теодолитами и вариационными
станциями.
При геологической разведке измеряют абсолютные
 и относительные (по отношению к какой-нибудь
исходной (опорной) точке и относительные (по отношению к какой-нибудь
исходной (опорной) точке  ) элементы. ) элементы.
Приборы для магнитной разведки (магнитометры) характеризуются
разнообразием принципов устройства. В основном используются четыре
типа магнитометров - оптико-механические, феррозондовые, протонные
и квантовые.
Чувствительная магнитная система оптико-механических магнитометров
состоит из магнита, который может вращаться либо вокруг вертикальной
оси (подобно магнитной стрелке в компасе) для измерений приращений
горизонтальной составляющей в двух точках ( ), либо
вокруг горизонтальной оси для измерения приращений вертикальной составляющей
( ), либо
вокруг горизонтальной оси для измерения приращений вертикальной составляющей
( ). Углы отклонения ). Углы отклонения 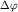 , пропорциональные , пропорциональные
 или или  , определяются с помощью специальной
оптической системы. Сняв отсчеты по магнитометру в двух точках ( , определяются с помощью специальной
оптической системы. Сняв отсчеты по магнитометру в двух точках (
 и и  ), можно определить приращение, например, ), можно определить приращение, например,
 ,
где ,
где  - цена деления магнитометра. Ее определяют путем
градуировки с помощью эталонировочных магнитов. На этом принципе
был построен магнитометр, названный весами Шмидта, применявшийся
в магниторазведке для измерения - цена деления магнитометра. Ее определяют путем
градуировки с помощью эталонировочных магнитов. На этом принципе
был построен магнитометр, названный весами Шмидта, применявшийся
в магниторазведке для измерения  свыше 50 лет. Среди
отечественных магнитометров к этому типу относились полевые приборы
М-2, М-18, М-27, а также приборы для измерения магнитных cвойств
образцов М-14 и астатические магнитометры. Погрешности в определениях свыше 50 лет. Среди
отечественных магнитометров к этому типу относились полевые приборы
М-2, М-18, М-27, а также приборы для измерения магнитных cвойств
образцов М-14 и астатические магнитометры. Погрешности в определениях
 с помощью таких магнитометров составляют с помощью таких магнитометров составляют  нТл. нТл.
Измерителем поля в феррозондовом магнитометре является феррозонд (или магнитомодулярный
датчик), представляющий собой катушку с ферромагнитным сердечником.
Первичная обмотка сердечника возбуждается от вспомогательного звукового
генератора частотой 200 гц. Под его воздействием меняется магнитная
проницаемость материала сердечника, а это, вследствие законов индукции,
приводит к тому, что во вторичной обмотке катушки возникает электродвижущая
сила, пропорциональная вектору напряженности магнитного поля Земли,
направленному вдоль оси сердечника.
Для измерения вертикальной составляющей феррозонд
ориентируется по вертикали особым маятником, помещенным в кардановом
подвесе. Последний снабжен демпфирующим устройством для быстрого
затухания колебаний. Феррозонд подключается к измерительному блоку.
В нем помещен звуковой генератор, переключатель поддиапазонов, переключатель
компенсации магнитного поля, измерительный индикаторный прибор.
Среди отечественных магнитометров к этому типу относится магнитометр
М-17, предназначенный для измерения  с точностью
до 1 с точностью
до 1  5 нТл. 5 нТл.
На феррозондовом принципе изготовлялись отечественные
аэромагнитометры - АЭМ-49, АМ-13, АММ-13, АСТ-46, АМФ-21 и др.
В аэромагнитометрах измерительный феррозонд с помощью особых карданных
устройств и двух дополнительных взаимно перпендикулярных феррозондов
устанавливается вдоль полного вектора напряженности магнитного поля
Земли. Он помещается в специальной гондоле и буксируется за самолетом
на кабеле длиной 40 - 50 м. Электрический сигнал с этого блока
по кабелю попадает на пульт магнитометра, установленный на самолете,
где усиливается электронным усилителем, выпрямляется и попадает на
автоматическое компенсационное устройство и особый самописец. На
ленте, кроме напряженности поля  , записываются высота
полета, марки времени, отметки ориентиров или синхронных аэрофотоснимков.
Аэромагнитометры устанавливаются на самолетах легкого типа или на
вертолетах. Погрешности измерений , записываются высота
полета, марки времени, отметки ориентиров или синхронных аэрофотоснимков.
Аэромагнитометры устанавливаются на самолетах легкого типа или на
вертолетах. Погрешности измерений  -аэромагнитометрами
не превышают -аэромагнитометрами
не превышают  20 нТл. 20 нТл.
Чувствительным элементом протонного магнитометра является жидкость,
богатая протонами (вода, спирт). Сосуд с этой жидкостью помещается
внутри питающей (поляризационной) катушки, в которой с помощью постоянного
тока от батарейки создается магнитное поле. Его надо направить перпендикулярно
полному вектору магнитного поля Земли в данной точке (  ).
Жидкость "намагничивается" в течение примерно двух секунд, и все
протоны, которые можно считать элементарными магнитиками, устанавливаются
вдоль намагничивающего поля. Затем намагничивающее поле быстро выключается.
Протоны, стремясь установиться вдоль вектора ).
Жидкость "намагничивается" в течение примерно двух секунд, и все
протоны, которые можно считать элементарными магнитиками, устанавливаются
вдоль намагничивающего поля. Затем намагничивающее поле быстро выключается.
Протоны, стремясь установиться вдоль вектора  , колеблются
(прецессируют) вокруг него и индуцируют в измерительной катушке очень
слабую ЭДС, частота которой пропорциональна величине напряженности
поля , колеблются
(прецессируют) вокруг него и индуцируют в измерительной катушке очень
слабую ЭДС, частота которой пропорциональна величине напряженности
поля  . На этом принципе были изготовлены отечественные
магнитометры: полевой (МПП-203) с погрешностью измерений . На этом принципе были изготовлены отечественные
магнитометры: полевой (МПП-203) с погрешностью измерений  до
до  2 нТл, а также аэромагнитометр (МСС-214) и гидромагнитометр
(ММП-3) с погрешностями порядка 2 нТл, а также аэромагнитометр (МСС-214) и гидромагнитометр
(ММП-3) с погрешностями порядка  3 нТл. 3 нТл.
Назад| Вперед
|

