В результате гравиразведки рассчитываются аномалии
силы тяжести, обусловленные теми или иными плотностными неоднородностями,
а влияние притяжения всей Земли и окружающего рельефа исключается
вычитанием нормального поля и введением редукций (см. 1.2.3). Поэтому
в математической теории гравиразведки расcчитываются аномалии от
тел простых форм: шара, горизонтального цилиндра, вертикального уступа,
вертикального цилиндра и т.д. без учета притяжения всей Землей.
Нахождение аномалий силы тяжести и вторых производных
потенциала от тел известной формы, глубины залегания, размера и
плотности носит название прямой задачи гравиразведки. Определение
местоположения, формы, глубины залегания, размеров и плотности тел
по известным аномалиям 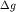 или вторых производных потенциала
силы тяжести называется обратной задачей гравиразведки. или вторых производных потенциала
силы тяжести называется обратной задачей гравиразведки.
Аномалия силы тяжести, вызванная притяжением
тел известной формы, размера и плотности, может быть вычислена на
основании закона всемирного притяжения (закон Ньютона).
Пусть в координатной системе
xyz ось z направлена вниз к центру Земли. Ставится
задача определить в точке наблюдения А(x,y,z) аномальную силу тяжести (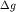 ), т.е. вертикальную
составляющую силы притяжения Землей единицы массы ( ) элементарной массой dm, находящейся в точке
M (x',y',z') (рис. 1.2). ), т.е. вертикальную
составляющую силы притяжения Землей единицы массы ( ) элементарной массой dm, находящейся в точке
M (x',y',z') (рис. 1.2).
 | | Рис.1.2 К определению аномалий силы тяжести от элементарной массы |
По закону Ньютона притяжение единичной массы равно:
где  - гравитационная постоянная, - гравитационная постоянная,  - расстояние
между точками (см. 1.4). - расстояние
между точками (см. 1.4).
Аномалия 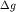 является проекцией
вектора f на ось z: является проекцией
вектора f на ось z:
 | (1.6) |
где из треугольника ABM  . Это же выражение можно получить с помощью
потенциала W=Gdm/r. В самом деле: . Это же выражение можно получить с помощью
потенциала W=Gdm/r. В самом деле:
 | (1.7) |
Обозначив плотность притягивающей массы через
 , а ее объем через dV, можно записать , а ее объем через dV, можно записать
 | (1.8) |
Такова будет аномалия силы
тяжести, обусловленная массой, расположенной в пустоте. В природных
условиях аномальные включения расположены во вмещающей среде с некоторой
плотностью  , поэтому под массой dm надо понимать
избыточную массу , поэтому под массой dm надо понимать
избыточную массу  . .
Отсюда
 | (1.9) |
где  - избыточная плотность.
- избыточная плотность.
При  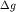 имеет положительный знак, т.е. наблюдается увеличение притяжения
и положительные аномалии имеет положительный знак, т.е. наблюдается увеличение притяжения
и положительные аномалии 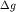 . При . При  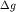 имеет отрицательный знак, т.е.
наблюдается уменьшение притяжения и отрицательные аномалии имеет отрицательный знак, т.е.
наблюдается уменьшение притяжения и отрицательные аномалии 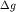 . .
В принципе аномалия, созданная любым телом, может
быть определена интегралом по объему тела:
 | (1.10) |
т.е. суммой притяжений всех элементарных объемов, из которых состоит
тело.
Рассмотрим несколько прямых и обратных задач для
тел простой геометрической формы.
1. Прямая задача. Пусть однородный шар радиуса  и плотности
и плотности  расположен на глубине расположен на глубине 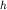 в среде с плотностью
в среде с плотностью  (для простоты центр находится
на оси z, а наблюдения проводятся по оси x
в точке P) (рис. 1.3). (для простоты центр находится
на оси z, а наблюдения проводятся по оси x
в точке P) (рис. 1.3).
 | | Рис.1.3 Гравитационное поле шара |
Формула для вычисления  может быть получена
из (1.6) - (1.9) путем замены элемента может быть получена
из (1.6) - (1.9) путем замены элемента  массой шара в силу
того, что притяжение однородным шаром происходит так, как если бы
вся масса была сосредоточена в центре шара.
Учтя, что x'=y'=0,z'=h,y=z=0, получим для шара массой шара в силу
того, что притяжение однородным шаром происходит так, как если бы
вся масса была сосредоточена в центре шара.
Учтя, что x'=y'=0,z'=h,y=z=0, получим для шара
 | (1.11) |
График 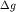 будет иметь максимум над
шаром (x=0) и асимптотически стремиться к нулю при удалении
от шара. В плане изолинии будет иметь максимум над
шаром (x=0) и асимптотически стремиться к нулю при удалении
от шара. В плане изолинии  будут иметь вид концентрических
окружностей. будут иметь вид концентрических
окружностей.
Вторая производная (градиент аномалии по профилю
наблюдений) равна:
Вид кривой Wxz может быть легко
получен путем графического построения из кривой 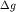 .
График Wxz имеет перед шаром максимум, за шаром
- минимум, над центром шара - ноль. .
График Wxz имеет перед шаром максимум, за шаром
- минимум, над центром шара - ноль.
2. Обратная задача. Из (1.11) максимум
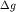 над центром шара (x=0) равен над центром шара (x=0) равен  . .
Для точки, удаленной от максимума на расстояние
x1/2, имеющей  , можно записать следующее
уравнение: , можно записать следующее
уравнение:
Решив последнее уравнение, получим формулу для
определения глубины залегания центра шара h=1,3x1/2. Зная 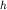 , легко найти избыточную массу ( , легко найти избыточную массу ( ): ):
 . .
Так как  то, зная избыточную плотность то, зная избыточную плотность  , можно рассчитать объем ( , можно рассчитать объем ( ) и радиус
шара ( ) и радиус
шара ( ). Так, радиус равен: ). Так, радиус равен:
где  - в миллигалах, - в миллигалах,
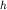 - в метрах, - в метрах,  - в тоннах / куб. метр (г/см3). - в тоннах / куб. метр (г/см3).
1.Прямая задача. Рассмотрим бесконечно длинный круговой горизонтальный
цилиндр радиуса  , расположенный вдоль оси y (рис.
1.4). Ось наблюдений ( x) направим вкрест простирания цилиндра. , расположенный вдоль оси y (рис.
1.4). Ось наблюдений ( x) направим вкрест простирания цилиндра.
 | | Рис.1.4 Гравитационное поле бесконечно длинного кругового горизонтального цилиндра |
Притяжение однородным цилиндром
происходит так же, как если бы вся его масса была сосредоточена вдоль
вещественной линии, расположенной вдоль оси цилиндра, с массой единицы
длины, равной  . Используя (1.10), можно получить формулы для . Используя (1.10), можно получить формулы для 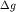 и и  : :
 | (1.12) |
Графики 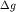 и и  над цилиндром и шаром внешне похожи (см. рис. 1.3 и 1.4). В плане
изолинии
над цилиндром и шаром внешне похожи (см. рис. 1.3 и 1.4). В плане
изолинии 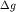 над цилиндром будут вытянутыми параллельными
линиями. над цилиндром будут вытянутыми параллельными
линиями.
2. Обратная задача.
Из (1.10 и 1.12) можно при х=0 получить  . Отсюда . Отсюда
и  , ,  ,
т.е. глубина залегания цилиндра равна расстоянию от точки максимума ,
т.е. глубина залегания цилиндра равна расстоянию от точки максимума
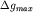 до точки, где до точки, где  . .
Определив 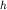 и зная
избыточную плотность, можно рассчитать и зная
избыточную плотность, можно рассчитать
и радиус цилиндра:
Зная  , можно получить глубины залегания
верхней hв=h-R и нижней
hн=h+R кромок цилиндра. Нетрудно
вычислить выражение и для , можно получить глубины залегания
верхней hв=h-R и нижней
hн=h+R кромок цилиндра. Нетрудно
вычислить выражение и для  . .
Назад| Вперед
|

