|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Приложение
Международный символ групп симметрии - символ
Германа- Могена - состоит как
минимум из трех позиций, на которых фиксированы
обозначения неэквивалентных особых направлений:
осей симметрии (поворотных и инверсионных) и
нормалей к плоскостям симметрии.
Поворотные оси симметрии регистирируют
соответствующи-ми их порядку арабскими цифрами (L4
= 4, L1 = 1). При обозначении инверсионной оси
над цифрой ставится черточка ( 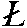 3 = 3 = 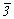 читается "три с чертой",
читается "три с чертой", 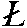 4= 4= 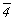 ); в
случае зеркальной оси - кружок ( ); в
случае зеркальной оси - кружок ( 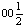 3 = 3 = 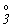 -
читается "три зеркальная", -
читается "три зеркальная", 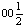 2 = 2 = 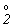 ). Однако
в стандартных символах используются только
инверсионные оси. Вместо инверсионной оси ). Однако
в стандартных символах используются только
инверсионные оси. Вместо инверсионной оси 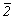 в символе записывается
совпадающая с ней нормаль к плоскости симметрии
- m (англ. mirror - зеркало). в символе записывается
совпадающая с ней нормаль к плоскости симметрии
- m (англ. mirror - зеркало).
Если ось симметрии (n) совпадает с нормалью к
плоскости (m), то они фиксируются на одной
позиции символа в виде дроби 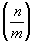 , где в числителе - обозначение оси
симметрии, а в знаменателе - нормали к плоскости
(например, L3P^ = , где в числителе - обозначение оси
симметрии, а в знаменателе - нормали к плоскости
(например, L3P^ =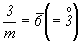 ,
L2PC = ,
L2PC = 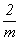 ). Однако,
если ось является порожденной другими
элементами симметрии, записанными в символе, ее,
как правило, опускают, оставляя лишь букву m.
Нельзя опустить лишь обозначение главной оси в
группах средней категории, указывающей на
принадлежность группы к той или иной сингонии ). Однако,
если ось является порожденной другими
элементами симметрии, записанными в символе, ее,
как правило, опускают, оставляя лишь букву m.
Нельзя опустить лишь обозначение главной оси в
группах средней категории, указывающей на
принадлежность группы к той или иной сингонии
(3L23PC = 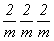 = mmm,
L44L25PC = = mmm,
L44L25PC =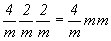 ,
L2PC = ,
L2PC = 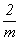 ). ).
Символы групп низшей категории
Поскольку в группах ромбической системы
все три особые направления неэквивалентны и
служат координатными осями X, Y и Z, каждое из них
регистрируется на определенной позиции символа:
на 1-й позиции - особое направление вдоль оси Х,
на 2-й позиции - особое направление вдоль оси У,
на 3-й позиции - особое направление вдоль оси Z.
Например, символ mm2 (= L22P) указывает
на то, что вертикальная ось Z выбрана вдоль
поворотной оси 2-го порядка. Очевидно, что символы
m2m и 2mm указывают на нестандартную
установку ромбической группы симметрии: в первом
случае поворотная ось направлена вдоль оси Y, во
втором - вдоль оси Х.
Группы моноклинной системы характеризуются
единственным особым направлением, которое и
фиксируется на одной из позиций символа. Чтобы
показать, с какой из координатных осей связано
единственное особое направление, можно на не
занятые особыми направлениями позиции символа
поставить единицы - оси 1-го порядка (L2 = 2 =
211 = 112 = 121).
В группах триклинной системы особые
направления отсутствуют. Поэтому в символе
записывают лишь ось 1-го порядка - поворотную или
инверсионную ( L1= 1, 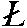 1 = С = 1 = С = 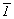 ). ).
Символы групп симметрии средней
категории
Обязательной принадлежностью групп симметрии
средней категории тетрагональной и
гексагональной сингоний является
единственная ось высшего порядка, вдоль которой
обычно выбирают координатную ось Z. Именно это
главное особое направление и записывается на 1-й
позиции международного символа. На 2-й позиции
фиксируются эквивалентные особые направления
вдоль горизонтальных координатных осей X = Y (= U);
на 3-й позиции - особое направление, расположенное
под углом  /2
к побочным координатным особым направлениям (где /2
к побочным координатным особым направлениям (где
 -
элементарный угол поворота, заданный главной
осью, фиксированной на 1-й позиции символа).
Элементы симметрии, представленные этим особым
направлением, - результат взаимодействия
элементов симметрии 1-й и 2-й позиций символа. Если
a /2 = 45o (главная ось 4 или -
элементарный угол поворота, заданный главной
осью, фиксированной на 1-й позиции символа).
Элементы симметрии, представленные этим особым
направлением, - результат взаимодействия
элементов симметрии 1-й и 2-й позиций символа. Если
a /2 = 45o (главная ось 4 или 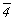 ), то направление 3-й позиции называют
диагональным, при ), то направление 3-й позиции называют
диагональным, при  /2 = 30o (ось 6 или /2 = 30o (ось 6 или 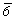 ) - апофемальным. ) - апофемальным.
Для осей 3 и 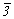 апофемальное направление (
апофемальное направление ( /2 = 60o ) совпадает с
координатным U. Таким образом, охарактеризовав в
символе одно из координатных (X, Y или U),
автоматически характеризуем и апофемальное
направление. В этом случае 3-я позиция символа не
заполняется (например, L33P = 3m, но L44L2
= 422, в последней группе координатные и
диагональные особые направления - оси 2-го
порядка - неэквивалентны, поэтому каждая из них
регистрируется на соответствующей позиции
символа). /2 = 60o ) совпадает с
координатным U. Таким образом, охарактеризовав в
символе одно из координатных (X, Y или U),
автоматически характеризуем и апофемальное
направление. В этом случае 3-я позиция символа не
заполняется (например, L33P = 3m, но L44L2
= 422, в последней группе координатные и
диагональные особые направления - оси 2-го
порядка - неэквивалентны, поэтому каждая из них
регистрируется на соответствующей позиции
символа).
Напомним, что, поскольку координатные оси X и Y в
точечных группах средней категории предпочитают
выбирать вдоль поворотных осей 2-го порядка,
стандартным символом класса 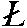 42L22P будет 42L22P будет 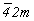 , при этом нормали к плоскостям
симметрии окажутся на 3-й, диагональной позиции
символа. Однако в группах гексагональной
сингонии при выборе координатных направлений
предпочтение оказывают нормалям к плоскостям
симметрии (m). Поэтому "официальным"
символом точечной группы L33L23PvPh
= = , при этом нормали к плоскостям
симметрии окажутся на 3-й, диагональной позиции
символа. Однако в группах гексагональной
сингонии при выборе координатных направлений
предпочтение оказывают нормалям к плоскостям
симметрии (m). Поэтому "официальным"
символом точечной группы L33L23PvPh
= = 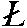 6 3L23P
будет 6 3L23P
будет 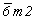 , а не , а не 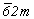 . .
Символы групп симметрии высшей
категории
В группах кубической сингонии все три
координатные особые направления эквивалентны (Х
= Y = Z). Поэтому они в международном символе
фиксируются на одной - первой - позиции.
Диагональные особые направления, проходящие по
биссектрисам углов между координатными осями,
регистрируют на 3-й позиции. На 2-й позиции символа
записывают цифру "3", символизирующую
обязательную для всех групп кубической сингонии
четверку осей 3-го порядка (3L44L36L2
= 432, 3L44L36L23Pк6PdC =
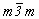 ). ).
Итак, в международных символах фиксируют в
основном порождающие элементы симметрии,
предпочитая в качестве таковых плоскости
симметрии. Если инверсионная ось имеет бо? льшую
величину симметрии (т.е. обладает большей
размножающей способностью), чем совпадающая с
ней ее поворотная составляющая, то в символе
регистрируется именно инверсионная ось
(например, вместо 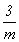 записывают
записывают 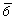 , вместо , вместо 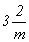 - - 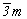 и вместо m3m - и вместо m3m - 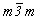 ).
При одинаковой размножающей способности
совпадающих поворотной и инверсионной осей в
символе фиксируется поворотная ось ( ).
При одинаковой размножающей способности
совпадающих поворотной и инверсионной осей в
символе фиксируется поворотная ось (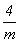 , а не , а не 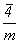 ). ).
Международные символы пространственных групп
симметрии в отличие от символов точечных групп
сопровождаются буквой, указывающей на тип
решетки Браве (Р - примитивный, С(А,В) -
базо - или бокоцентрированный, I - объемноцентрированный,
F - гранецентрированный). Кроме того, в
качестве подрешеточных элементов симметрии на
позициях символа могут появиться кроме
макроэлементов симметрии - зеркальных
плоскостей, поворотных осей и центра инверсии - и
трансляционные элементы симметрии: плоскости
скользящего отражения и винтовые оси - элементы
микросимметрии.
Обозначения групп симметрии Шенфлиса
Символика точечных групп симметрии,
предложенная немецким математиком А. Шенфлисом,
позволяет одной буквой с соответствующим нижним
индексом не только охарактеризовать весь набор
элементов симметрии конкретной точечной группы,
но и объединить родственные группы в отдельные
семейства.
Циклические группы - группы с единственным
особым направлением, представленным поворотной
осью симметрии, - обозначаются буквой С, с
нижним цифровым индексом n, соответствующим
порядку этой оси (например, С4 = L4 , C1
= L1)).
Группы с единственной инверсионной осью симметрии
сопровождаются нижним индексом i, например С3i
= 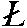 3, Ci = 3, Ci = 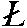 1. Если же
инверсионной оси предпочитают ее зеркальный
эквивалент, то группа с такими осями
обозначается Sn (от нем. spiegelaxe -
зеркальная ось), например S6 = C3i ,
S4 = C4i; при этом цифровой индекс n
всегда отвечает порядку сложной оси. 1. Если же
инверсионной оси предпочитают ее зеркальный
эквивалент, то группа с такими осями
обозначается Sn (от нем. spiegelaxe -
зеркальная ось), например S6 = C3i ,
S4 = C4i; при этом цифровой индекс n
всегда отвечает порядку сложной оси.
Группы симметрии с побочными -
перпендикулярными главному направлению - осями
2-го порядка обозначаются Dn, где
нижний индекс n соответствует не только
порядку главной поворотной оси, но и количеству
побочных осей 2-го порядка (например, D3 = L33L2
, D2 = 3L2 , в последней группе любая
из осей L2 может играть роль главной, две
другие, перпендикулярные ей, при этом окажутся
побочными).
Для обозначения зеркальных плоскостей
симметрии Шенфлис ввел дополнительные
подстрочные буквенные индексы:
v (от нем. vertical - вертикальный) - для
плоскостей, расположенных вдоль единственной
или главной оси симметрии, которая всегда
мыслится вертикальной 1 (L33P
= C3v);
h (от нем. horisontal - горизонтальный) - для
плоскости, перпендикулярной к главной оси
симметрии (L2PC = C2h);
s (от нем. spiegel - зеркало) - для плоскости
неопределенной ориентации, т.е. не фиксированной
ввиду отсутствия в группе иных элементов
симметрии (Р = Cs (= Pv = Ph));
d - для вертикальных плоскостей симметрии,
делящих пополам угол между побочными осями 2-го
порядка (D3d = L33L23PC, D2d = = 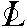 4( 4(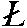 4)2L22Pd; в
последней группе нижний цифровой индекс n = 2
соответствует поворотной составляющей сложных
осей 4)2L22Pd; в
последней группе нижний цифровой индекс n = 2
соответствует поворотной составляющей сложных
осей 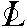 4 = 4 = 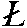 4). 4).
Если же вертикальные плоскости симметрии
проходят через побочные (горизонтальные) оси 2-го
порядка, неизбежно возникает четко
фиксированная по отношению к главной оси
горизонтальная плоскость h, которой и
отдается предпочтение в символе Шенфлиса (D3h
= L33L23PvPh). Индекс v
в группах Dn оказывается неоднозначным.
Группы симметрии с несколькими осями высшего
порядка - группы кубической сингонии -
обозначаются буквой О в случае, если они
содержат полный набор осей симметрии (3L44L36L2
- осевой комплекс октаэдра или куба), или буквой Т
- если в группе отсутствуют диагональные оси
симметрии (3L24L3 - поворотные
составляющие осевого комплекса тетраэдра).
Наличие в группе координатных или диагональных
плоскостей симметрии фиксируется в символе
Шенфлиса соответственно буквами h (среди
координатных плоскостей всегда присутствует
горизонтальная h) или d. Если в группе
имеются оба типа плоскостей, то в символе
фиксируются лишь координатные h (3L24L33PкC
= Th , 3 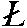 4 4L36Pd
= Td , 3L44L36L23Pк6PdC
= Oh). 4 4L36Pd
= Td , 3L44L36L23Pк6PdC
= Oh).
В обозначениях пространственных групп
симметрии появляются вверхние цифровые
индексы, отражающие ту последовательность, в
которой А.Шенфлис выводил пространственные
группы. И поскольку иной смысловой нагрузки эти
индексы не несут, в этом качестве они оказываются
недостаточно информа-тивны (например, 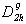 = Pbam, = Pbam, 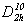 = Pccn, = Pccn, 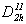 = Pbcm).
Однако, поскольку международные символы
пространственных групп могут видоизменяться с
преобразованием координатной системы (например, Сmc21
= A21ma), необходимо их сопровождать
символом Шенфлиса, не учитывающим ориентацию
пространственной группы относительно выбранной
координатной системы (A21ma = = Pbcm).
Однако, поскольку международные символы
пространственных групп могут видоизменяться с
преобразованием координатной системы (например, Сmc21
= A21ma), необходимо их сопровождать
символом Шенфлиса, не учитывающим ориентацию
пространственной группы относительно выбранной
координатной системы (A21ma = 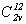 ) и однозначно указывающим на
определенную пространственную группу. ) и однозначно указывающим на
определенную пространственную группу.
| 
