1.1.2. Простые формы кристаллов
низшей и средней категорий
Простой формой
кристалла называют семейство граней,
взаимосвязанных симметрическими операциями
данного класса симметрии. Все грани, образующие
одну простую форму кристалла, должны быть равны
по размеру и форме. В кристалле могут
присутствовать одна или несколько простых форм.
Сочетание нескольких простых форм называется комбинацией.
- Закрытыми
называют такие формы, грани которых полностью
замыкают заключенное между ними пространство,
как, например, куб;
- Открытые простые
формы не замыкают пространство и не могут
существовать самостоятельно, а только в
комбинациях. Например, призма + пинакоид.
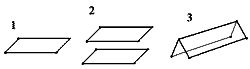 |
| Рис.6.
Простые формы низшей категории: моноэдр (1),
пинакоид (2), диэдр (3). |
В низших сингониях возможны следующие открытые
простые формы (рис. 6):
Моноэдр (от греч. "моно"- один,
"эдра"- грань) - простая форма, представленная
одной единственной гранью. Моноэдром является,
например, основание пирамиды.
Пинакоид (от греч."пинакс"-
доска) - простая форма, состоящая из двух равных
параллельных граней, часто обратно
ориентированных.
Диэдр (от греч."ди" - два, "эдр"-
грань) - простая форма, образованная двумя
равными пересекающимися (иногда на своем
продолжении) гранями, образующими "прямую
крышу".
Ромбическая призма -
простая форма , которая состоит из четырех
равных, попарно параллельных граней, которые в
сечении образуют ромб.
Ромбическая
пирамида - простая форма состоит из четырех
равных пересекающихся граней; в сечении также -
ромб.
Из закрытых простых форм низших сингоний
отметим следующие:
Ромбическая
дипирамида две ромбические пирамиды,
сложенные основаниями. Форма имеет восемь равных
граней, дающих в поперечном сечении ромб.
Ромбический
тетраэдр - простая форма, четыре грани которой
имеют форму косоугольных треугольников и
замыкают пространство.
В сингониях низшей категории кристаллы могут
иметь только 7 простых форм, перечисленных выше.
В сингониях средней категории из перечисленных
выше простых форм могут присутствовать только
моноэдр и пинакоид.
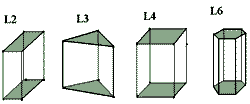 |
| Рис. 7.
Внешний вид призматических кристаллов: 1 - ромбическая призма; 2 - тригонльня призма; 3
- тетрагональная призма; 4 - гексаго- нальная призма. |
Открытыми простыми формами сингоний средней
категории будут призмы и пирамиды.
Тригональная призма
(от греч."гон"- угол) - три равных грани,
пересекающихся по параллельным ребрам и
образующих в сечении равносторонний
треугольник;
Тетрагональная
призма (от греч."тетра"- четыре) - четыре
равных попарно параллельных грани, образующих в
сечении квадрат;
Гексагональная
призма (от греч."гекса"- шесть) - шесть равных
граней, пересекающихся по параллельным ребрам и
образующих в сечении правильный шестиугольник.
Названия дитригональных, дитетрагональных и
дигексагональных получили призмы с удвоенным
числом граней, когда все грани равны, а
одинаковые углы между гранями чередуются через
один.
Пирамиды - простые формы
кристаллов средней категории могут быть, также
как и призмы, тригональными (и дитригональными),
тетрагональными (и дитетрагональными),
гексагональными( и дигексагональными). Они
образуют в сечении правильные многоугольники.
Грани пирамид располагаются под косым углом к
оси симметрии высшего порядка.
В кристаллах средней категории встречаются так
же закрытые простые формы. Таких форм несколько:
Дипирамиды - простые формы,
образованные двумя равными пирамидами,
сложенными основаниями. В таких формах
происходит удвоение пирамиды горизонтальной
плоскостью симметрии, перпендикулярной главной
оси симметрии высшего порядка (рис. 8). Дипирамиды,
как и простые пирамиды, в зависимости от порядка
оси могут иметь различные формы сечения. Они
могут быть тригональными, дитригональными,
тетрагональными, дитетрагональными,
гексагональными и дигексагональными.
Ромбоэдр - простая форма, которая состоит из шести
граней в виде ромбов и напоминает вытянутый или сплющенный по диагонали куб.
Он возможен только в тригональной сингонии. Верхняя и нижняя группа граней
повернуты относительно друг друга на угол 60о таким образом, что
нижние грани располагаются симметрично между верхними.
В сингониях средней категории вероятны также скаленоэдры, тетрагональный
тетраэдр и трапецоэдры.
Оглавление| Назад|
Следующая страница
|

