Термоселективная методика датирования кварца по Al-парамагнитным центрам и уточнение хронологии извержений вулкана Эльбрус

Глава 2. Определение рекомбинационных параметров Ea, K0 и среднего времени жизни τ для Al-парамагнитных центров в кристаллической структуре α-кварца.

В данной работе исследована динамика термического разрушения [AlO₄^-/h⁺] парамагнитных центров в кварце методом изотермических лабораторных отжигов. Работы по измерению рекомбинационных параметров E_a, K₀ и среднего времени жизни τ для Al-парамагнитных центров проводились на образцах кварца, отобранного из эффузивных пород Эльбруса, гранитов Эльджуртинского массива (Северный Кавказ) и месторождения <Желанное> (Приполярный Урал). Изотермические отжиги образцов кварца проводились в температурном интервале 150 - 400^OС.

В качестве примера серии изотермических отжигов на рис. 2 приведены графики отжигов образца кварца N 1119-1 (Эльбрус) при различных температурах.

Классические модели рекомбинации парамагнитных центров предполагают снижение их концентрации согласно либо экспоненциальному, либо гиперболическому закону. Однако полученные экспериментальные зависимости концентрации центров от времени отжига убедительно продемонстрировали, что ни одна из этих моделей не может их описать с разумной степенью точности.

Задача моделирования данных изотермических отжигов в данной работе была решена на основе представления о наличии в кристаллической решетке кварца нескольких типов Al-парамагнитных центров. Математические зависимости, использованные в данной работе для описания процесса рекомбинации концентраций [AlO₄^-/h⁺] парамагнитных центров, состояли из суммы двух либо трех экспоненциальных и гиперболических функций в различных возможных комбинациях. Моделирование процессов изотермического отжига при каждой температуре производилось путем подбора значений начальных концентраций yi и величин ki до достижения максимальной сходимости расчетных значений и данных эксперимента. Необходимым условием также принималась неизменность набора значений первичных концентраций yi всех типов центров для каждого отдельного образца во всем интервале температур. Окончательным критерием адекватности той или иной модели экспериментальным кривым отжига служил минимальный разброс данных на диаграмме Аррениуса.

Были рассмотрены двухкомпонентные моделирующие функции:

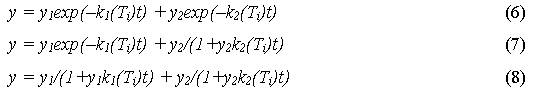
Модели давали существенное улучшение сходимости моделирующей функции и экспериментально полученных данных по сравнению с аппроксимацией одной экспоненциальной или гиперболической зависимостью. Однако при относительно высоких температурах отжига выявлялась их несостоятельность. Отклонения моделирующей функции от экспериментальных данных намного превышали ошибку измерения на начальном этапе высокотемпературных отжигов - модели не могли отразить резкого снижения концентрации, либо требовали изменения соотношения первичных концентраций y₁ : y₂ для одного образца при разных температурах отжига, что противоречило поставленной задаче.

Рассматривались также все возможные трехкомпонентные моделирующие функции. Наиболее корректной для аппроксимации результатов отжигов из всех опробованных моделей признана модель суммы двух экспоненциальных и гиперболической функций:

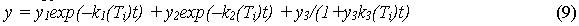
Все другие сочетания экспоненциальных и гиперболических функций приводят к небольшим, но систематическим отклонениям. Модель, состоящая из суммы двух экспоненциальных и гиперболической функций позволяет рассчитать параметры рекомбинации для всех трех типов [AlO₄^-/h⁺] парамагнитных центров. Модель приводит к выделению в составе [AlO₄^-/h⁺] центров с низкой, средней и высокой температурной устойчивостью, отвечающих первой, второй и третьей зависимостям в уравнении (9). Такие типы центров имеет смысл называть также короткоживущими, среднеживущими и долгоживущими [AlO₄^-/h⁺] парамагнитными центрами соответственно.

На рис. 3 приведен пример аппроксимации моделью суммы двух экспоненциальных и гиперболической функций данных изотермического отжига образца N 1119-1 кварца вулканитов Эльбруса при 185^OС. Диаграмма Аррениуса для всех трех типов [AlO₄^-/h⁺] парамагнитных центров образца кварца N 1119-1 приведена на рис. 4.

На основании полученных данных сформулировано первое защищаемое положение: Парамагнитные центры [AlO₄^-/h⁺] в кристаллической структуре α-кварца, образующиеся в результате замещения Al ╜ Si, представляют собой комплекс из трех типов центров - короткоживущего, среднеживущего и долгоживущего, различающихся по термической устойчивости. Суммарная термическая устойчивость [AlO₄^-/h⁺] парамагнитных центров в реальных образцах α-кварца зависит от количественных долевых соотношений между типами центров.

Значения рекомбинационных параметров E_a и K₀, средних времен жизни центров τ, а также первичных концентраций y₁, y₂, y₃, использованные в данной работе для датирования, рассчитаны с использованием в качестве моделирующей зависимости суммы двух экспоненциальных и гиперболической функций.

В табл. 2 приведены относительные концентрации трех типов [AlO₄^-/h⁺] парамагнитных центров: y₁, y₂, y₃ для кварца различного происхождения.

Таблица 2. Относительные первичные концентрации трех типов [AlO4-/h+] парамагнитных центров.
Кварц	y1	y2	y3
Вулканиты Эльбруса	0.41	0.34	0.25
Эльджуртинский гранит	0.49	0.31	0.20
Месторождение <Желанное>	-	0.45	0.55

Рекомбинационные параметры E_a и K₀ для трех типов [AlO₄^-/h⁺] парамагнитных центров в кварце приведены в табл. 3.

Таблица 3. Значения Ea и K0 для трех типов [AlO4-/h+] парамагнитных центров в кварце. I - кварц Эльбрусских эффузивных пород, II - кварц Эльджуртинского гранитного массива, III - кварц месторождения <Желанное>.
Короткоживущий тип центров
	Ea, эВ	lnK0	K0, с-1
I	1,21 0,07	23,21 0,71	1,2E+10
II	1,05 0,03	19,29 0,55	2,4E+08
III	-	-	-
Среднеживущий тип центров
I	1,33 0,06	23,92 2,52	2,5E+10
II	1,58 0,12	30,53 2,26	1,8E+13
III	1,22 0,02	18,06 0,09	7,0E+07
Долгоживущий тип центров
I	1,45 0,02	28,81 1,74	3,3E+12
II	1,77 0,08	34,47 1,52	9,4E+14
III	1,65 0,02	25,39 0,05	1,1E+11

В табл. 4 приведены значения τ для трех типов [AlO₄^-/h⁺] парамагнитных центров. Величины τ рассчитаны для температурных условий Эльбруса (Т = 1.5^OС) для всех образцов, кроме кварца месторождения <Желанное>; для последнего значения τ взяты для Т = -4^OС - условий месторождения <Желанное> на приполярном Урале.

Таблица 4. Значения τ для трех типов [AlO4-/h+] парамагнитных центров в кварце. I - кварц Эльбрусских эффузивных пород, II - кварц Эльджуртинского гранитного массива, III - кварц месторождения <Желанное>.
	τ1, лет	τ2, лет	τ3, лет
I	45 000	3 800 000	19 500 000
II	2 500	185 500 000	27 700 000 000
III	-	12 200 000	33 100 000 000 000

Разница в значениях рекомбинационных параметров для каждого из трех типов [AlO₄^-/h⁺] парамагнитных центров в кварце различного генезиса значительна. Это отчетливо проявляется в рассчитанных по ним величинах среднего времени жизни τ (табл. 4). Причиной таких различий, вероятно, являются разные - по продолжительности и физико-химическим параметрам - условия кристаллизации кварца эффузивных пород Эльбруса, Эльджуртинских гранитов и гидротермально-метасоматических пород месторождения <Желанное>. Фактором, который может оказывать значительное влияние на процессы рекомбинации [AlO₄^-/h⁺] парамагнитных центров в кварце различного генезиса, является степень совершенства кристаллической структуры. Наиболее важны два параметра - блочность и плотность дислокаций. Этими параметрами определяются, с одной стороны, средняя длина каналов в кристаллической структуре, и, с другой стороны, количество дополнительных, не связанных с ионами - примесями, электронных ловушек. Длина каналов ограничивает подвижность ионов - компенсаторов заряда, а связанные с дислокациями электронные ловушки характеризуются большим диапазоном энергий, т.е. глубиной <потенциальных ям>.

Сравнительно низкое значение энергии активации для короткоживущего типа [AlO₄^-/h⁺] парамагнитных центров в кварце Эльджуртинского гранита - 1,05 эВ - может быть обусловлено продолжительным процессом кристаллизации, характерным для интрузивных образований. При этом электронные и дырочные центры образуют комплексные пары и имеют время для упорядочения и уменьшения среднего расстояния между парными центрами. В результате образованные комплексные центры оказываются менее термически устойчивыми и характеризуются значением τ 2.5 тыс. лет (для 1.5^oС).

Параметры рекомбинации, на основе которых рассчитана величина среднего времени жизни τ для среднеживущих [AlO₄^-/h⁺] парамагнитных центров в кварце Эльджуртинского гранита, близки к величинам E_a и K_o, полученным в работе Шабалина Р.В. (2004), где для их определения использовались образцы кварца, выделенные из керна скважины СГ-1. Современная температура гранитного массива на глубинах отбора проб составляет 55^oС и выше. Согласно трехкомпонентной модели [AlO₄^-/h⁺] парамагнитных центров, в данной природной системе реализованы условия для накопления лишь средне- и долгоживущего типов центров. Соответственно, полученные в работе Шабалина Р.В. (2004) параметры рекомбинации (E_a = 1,7 эВ и K₀ = 8,2^.10¹⁴ с^-1), должны представлять усреднение (с учетом долевых соотношений) рекомбинационных параметров, определенных для средне- и долгоживущего типов центров кварца Эльджуртинского гранита в данной работе (табл. 3). Оба определения хорошо согласуются друг с другом.

Величины τ, определенные для долгоживущего типа центров в кварце Эльджуртинского гранита и месторождения <Желанное>, очевидно, не имеют геологического смысла. Тем не менее они отражают вероятность рекомбинации [AlO₄^-/h⁺] парамагнитных центров в условиях дефицита необходимых для этого электронов и ионов - компенсаторов заряда. Это ярко проявлено для кварца месторождения <Желанное>. Величина τ, равная 3,31∙10¹³ лет, определенная для долгоживущего типа Al-парамагнитных центров в кварце месторождения <Желанное>, отражает математически ничтожную вероятность рекомбинации части [AlO₄^-/h⁺] парамагнитных центров.

Второе защищаемое положение: Параметры рекомбинации и средние времена жизни для [AlO₄^-/h⁺] парамагнитных центров α-кварца вулканитов Эльбруса составили: E_a=1,21 эВ, K₀=1,2∙10¹⁰ с^-1 и τ=45 тыс. лет (при 1,5^-1С) для короткоживущего типа центров; E_a=1,33 эВ, K₀=2,5∙10¹⁰ с^-1 и τ=3,8 млн. лет (при 1,5^-1С) для среднеживущего типа центров; E_a=1,45 эВ, K₀=3,3∙10¹² с^-1 и τ=19,5 млн. лет (при 1,5^-1С) для долгоживущего типа центров.