| КИНЕМАТИКА СДВИГОВ ВИЛСОНА ("ТРАНСФОРМНЫХ РАЗЛОМОВ") | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Схема гравитационных аномалий центральной части Атлантики IntRes |
Анализ данных по строению и эволюции трансформных разломов разных групп показывает, что их кинематические характеристики, зависящие в целом от самых различных факторов, могут быть сведены к параметрам, которые, так или иначе, описывают изменение геометрии порождающих трансформы активных областей ( Тевелев, 1996). Управляющими факторами кинематического поведения трансформных сдвигов являются скоростные характеристики зон разрастания (или поглощения), степень скоростной асимметрии и геометрия активных зон. В разных группах трансформных сдвигов роль и значение этих параметров неодинаковы. Кинематика вилсоновских сдвигов типа хребет-хребет В трансформных сдвигах этого типа активные движения имеют место только на тех отрезках разлома, которые расположены
между кулисно смещенными зонами разрастания. Для наблюдателей, находящихся в
пределах активного отрезка разлома, он представляется обычным сдвигом с
направлением движений, противоположным видимому смещению зон разрастания,
однако для наблюдателей из внешних углов рифт - трансформной системы их мгновенные движения выглядят обратными
по отношению к движениям в активной (центральной) части разлома, совпадая с видимым смещением зон
разрастания. Поскольку из соображений симметрии никакая система отсчета не
является предпочтительной, то во внешней системе координат направление мгновенных
движений по такому разлому принципиально неопределенно, и
это обстоятельство является фундаментальным для кинематики вилсоновских
сдвигов NB ! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
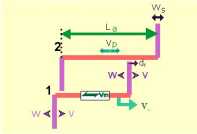 Кинематические характеристики сдвиговых зон трансформного типа (Тевелев, 1996) |
Амплитуда смещений вдоль разлома постоянна; досдвиговые маркеры смещаются в одном направлении, хотя сами сдвиги могут в постоянных тектодинамических условиях менять знак движения, уменьшаться в длине до нуля и снова разрастаться. К этим изменениям плановой конфигурации разломной зоны может добавляться ее продольная миграция, свободная, или заякоренная в одной из точек сдвиговой зоны. Скорость движений по сдвигу равна скорости расхождения блоков (плит), чьей латеральной границей сдвиг и является. При расчете кинематики трансформ используются параметры, показанные на рисунке cлева. Численное моделирование пространственно-временной эволюции трансформных сдвигов растяжения показало, что существует пять различных сценариев их развития, определяемых соотношениями скоростей разрастания активных зон, связанных трансформой (в случае СОХ - скоростей спрединга), и степенью их симметричности (рис. 1, см. ниже).
Эти данные можно обобщить следующим образом. Если под свойством размерной устойчивости понимать сохранение линейных размеров сдвиговой зоной по мере ее эволюции, а под свойством пространственной стационарности - ее заякоренность хотя бы в одной точке, разнообразие кинематического поведение Е-трансформ можно свести всего к четырем случаям (табл. 1), которые соответствуют пяти возможным типам скоростных матриц рифт-трансформных систем. Показанные на рисунке модели демонстрируют, что в условиях асимметричного разрастания «схлопывающиеся» трансформы эволюционно неустойчивы и, рано или поздно, переходят в трансформы растягивающиеся. Поэтому зоны трансформ типа хребет – хребет сравнительно редко содержат структуры продольного сжатия (например, внутритрансформные хребты). Долинная, «рифтовая» морфология большинства трансформ этого типа соответствует режиму продольного растяжения. 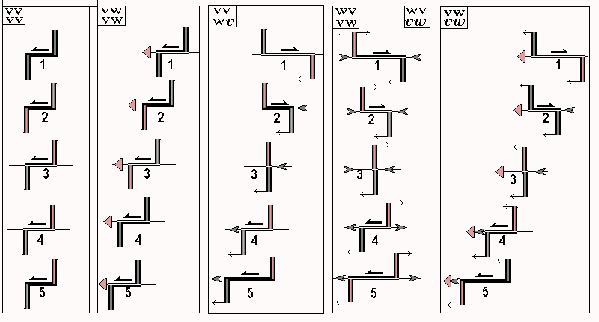 Рис 1. Эволюция Е-трансформ при разных значениях скоростей разрастания
Кинематика вилсоновских сдвигов типа дуга-дугаСдвиги типа дуга-дуга имеют конечную (хотя чаще всего непостоянную) длину, смещения вдоль модельного сдвига постоянны, мгновенная кинематика во внешней системе координат неопределенна. Смещения маркеров вдоль сдвига этого типа всегда совпадают со знаком движения на разломе. Последний, однако, как и в предыдущем случае, по мере эволюции сдвиговой зоны может меняться на противоположный при постоянном режиме конвергенции. Скорость движений по такому сдвигу равна скорости схождения блоков, чьей латеральной границей является сдвиг. Так же, как в предыдущим случае, сдвиговая зона данного типа может продольно мигрировать в свободном или заякоренном режиме. В областях сжатия с наклонными зонами поглощения выделяются три разных варианта их сопряжения:
Расчеты показывают, что при любых скоростных матрицах кинематический режим трансформ зависит только от геометрии зон поглощения (рис. 2). 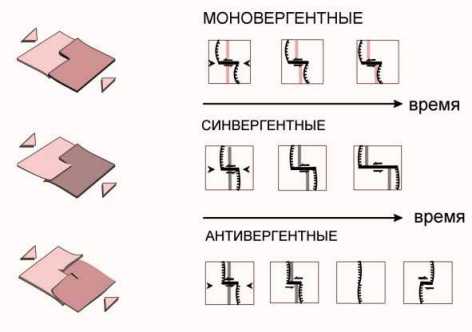 Рис. 2. Эволюция трансформ сжатия (тип дуга - дуга) при различной конфигурации структур поглощения В областях с моновергентными зонами поглощения всегда образуются устойчивые нестационарные трансформы, с синвергентными – стационарные неустойчивые растягивающиеся трансформы, а в антивергентных – стационарные неустойчивые схлопывающиеся трансформы, причем сама область поглощения эволюционирует в синвергентную, а знак движений на трансформе меняется на противоположный. Эти модели, основанные только на трансляционных деформациях, не учитывают стрейна в зонах сжатия, хотя последний в той или иной степени всегда имеет место. Очевидно, что в моновергентных областях активного сжатия приконтактовое поперечное сокращение блоков за счет стрейна может быть приблизительно одинаковым в обеих зонах; в этом случае кинематический тип трансформы не меняется, но уменьшается скорость миграции трансформы. В синвергентных областях на эту же величину уменьшается скорость наращивания трансформы, а в антивергентных областях на столько же уменьшается скорость “схлопывания”. Характеристика сдвигов этого типа представлена в табл. 2.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Сдвиговая зона Мертвого Моря - родина цивилизации
|
То обстоятельство, что «схлопывающиеся» трансформные сдвиги сжатия являются образованиями неустойчивыми и эволюционно переходят в сдвиги растягивающиеся, приводит к тому, что среди реальных компрессионных сдвигов преобладают разломные зоны с продольным растяжением, за счет которого обеспечивается щелевой, «рифтовый» облик большинства разломных сдвиговых зон. Структурно продольное растяжение континентальных сдвиговых зон сжатия реализуется за счет развития узких пулл-апартовых бассейнов и некоторых других структур присдвигового растяжения, вплоть до появления вулканических центров в общей обстановке коллизионного сжатия (Тевелев, Тевелев, 1996). В зонах океанских трансформных сдвигов сжатия к ним добавляются локальные спрединговые центры, возможно наследующие пулл-апарты. Самым знаменитым примером структур этого типа является Кайманов желоб в системе трансформ Сван-Ориенте на северной границе Карибской плиты. Кинематика вилсоновских сдвигов типа дуга-хребет (М-трансформ)Сдвиги типа хребет-дуга в кинематическом смысле отличаются от предыдущих. Модельный сдвиг этого типа имеет конечную длину и постоянную амплитуду движений на разломе. Направление смещений маркеров совпадает с направлением движением по трансформе, во внешней системе координат амплитуда смещений представляется нулевой. Знак движения по сдвигу по мере эволюции деформационной системы не меняется. Скорость движений по такому сдвигу равна той скорости, с которой обмениваются движениями и массами зоны разрастания и поглощения. Формальное кинематическое поведение М-трансформ вероятно совмещает характеристики С и Е-трансформ, однако в природе реализуется лишь небольшая часть потенциального многообразия. М-трансформы принципиально отличаются от остальных тем, что сопрягаемые ими активные зоны находятся по одну сторону от разлома. Такая конфигурация активной области, включающей М-трансформу, предполагает наличие более или менее замкнутых ограничений транслируемого блока (плиты) и второй трансформы в его тыловой части. Реально существующие М-трансформы обычно включены в блоковые (плитные) границы, составленные из отрезков нескольких тройных сочленений рифтовой, трансформной или коллизионной природы. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Top | FirstPage | Home |


