Next: 3.3. Неотслеживаемость. Электронные деньги
Up: 3. Криптографические протоколы
Previous: 3.1. Введение
Contents: Содержание
| |
``Воротится коза, постучится в дверь и запоет:
- Козлятушки, ребятушки!
Отопритеся, отворитеся!
Ваша мать пришла - молока принесла.
Козлятки отопрут дверь и впустят мать...
Волк подслушал как поет коза. Вот раз коза ушла, волк
подбежал к избушке и закричал толстым голосом:
- Вы детушки! Вы козлятушки!
Отопритеся, отворитеся,
Ваша мать пришла, молока принесла.
Козлята ему отвечают:
- Слышим, слышим - да не матушкин это голосок!...
Волку делать нечего. Пошел он в кузницу и велел себе
горло перековать, чтобы петь тонюсеньким голосом...
Только коза ушла, волк опять шасть к избушке,
постучался и начал причитывать тонюсеньким голосом:
- Козлятушки, ребятушки!
Отопритеся, отворитеся!
Ваша мать пришла - молока принесла.
Козлята отворили дверь, волк кинулся в избу и всех
козлят съел.''
|
|---|
``Волк и семеро козлят''.
Русская народная сказка.
Как уже отмечалось во введении, понятие целостности
информации, по-видимому, не допускает математической
формализации. В данном разделе мы
рассмотрим методы
обеспечения целостности на примере двух наиболее важных и
распространенных типов криптографических протоколов -
схем аутентификации и электронной подписи.
Назначение и суть протоколов
аутентификации (называемых
также протоколами идентификации) легко понять на следующем
примере. Представим себе информационную систему, которая
работает в компьютерной сети и обеспечивает доступ к
некоторым данным. У администратора системы имеется список
всех ее пользователей вместе с сопоставленным каждому из
них набором полномочий, на основе которых осуществляется
разграничение доступа к ресурсам системы. Ресурсами могут
быть, например, некоторые фрагменты информации, а также
функции, выполняемые системой. Одним пользователям может
быть разрешено читать одну часть информации, другим -
другую ее часть, а третьим - еще и вносить в нее
изменения. В данном контексте под обеспечением целостности
понимается предотвращение доступа к системе лиц, не
являющихся ее пользователями, а также предотвращение доступа
пользователей к тем ресурсам, на которые у них нет полномочий.
Наиболее распространенный метод разграничения доступа, парольная
защита, имеет массу недостатков. Их обсуждение стало общим
местом для текстов по компьютерной безопасности, поэтому мы
сразу перейдем к криптографической постановке задачи.
В протоколе имеются два участника - Алиса, которая должна
доказать свою аутентичность, и Боб, который эту
аутентичность должен проверить. У Алисы имеются два ключа
- общедоступный открытый 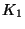 и секретный и секретный 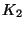 .
Фактически, Алисе нужно доказать, что она знает .
Фактически, Алисе нужно доказать, что она знает 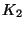 , и
сделать это таким образом, чтобы это доказательство можно
было проверить, зная только , и
сделать это таким образом, чтобы это доказательство можно
было проверить, зная только 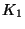 . .
Задача аутентификации уже обсуждалась в главе 2. Там же были
сформулированы основные требования, которым должен
удовлетворять стойкий протокол аутентификации. Напомним,
что для удовлетворения этих требований достаточно, чтобы
протокол аутентификации был доказательством с нулевым
разглашением. В главе 2 приведен протокол доказательства с
абсолютно нулевым разглашением для задачи ИЗОМОРФИЗМ
ГРАФОВ. Но этот протокол имеет неприемлемо большое с
практической точки зрения количество раундов обмена
сообщениями между Алисой и Бобом.
Ниже мы приводим протокол
Шнорра [1], один из наиболее
эффективных практических протоколов аутентификации. Для его
описания нам потребуются некоторые обозначения, которые
будут использоваться и в последующих разделах данной главы.
Пусть 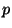 и и 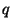 - простые числа такие, что - простые числа такие, что 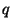 делит делит
 . Шнорр предлагает [1] использовать . Шнорр предлагает [1] использовать 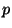 длины порядка
512 битов и длины порядка
512 битов и 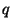 - длины порядка 140 битов. Пусть - длины порядка 140 битов. Пусть  таково, что таково, что  , ,  . Пусть . Пусть  и
и  . Задача
вычисления значения . Задача
вычисления значения 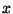 по
заданному значению по
заданному значению 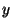 при известных при известных 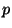 , , 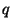 и и  называется задачей дискретного
логарифмирования (см. главу 4).
Для задачи дискретного логарифмирования на данный
момент не известно эффективных алгоритмов. Поэтому в
криптографии широко используется
гипотеза
о вычислительной трудности задачи дискретного логарифмирования. Сформулируем
ее более строго. Пусть
называется задачей дискретного
логарифмирования (см. главу 4).
Для задачи дискретного логарифмирования на данный
момент не известно эффективных алгоритмов. Поэтому в
криптографии широко используется
гипотеза
о вычислительной трудности задачи дискретного логарифмирования. Сформулируем
ее более строго. Пусть  - растущий
целочисленный параметр, число - растущий
целочисленный параметр, число 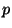 выбирается из множества
всех простых чисел длины выбирается из множества
всех простых чисел длины  таких, что таких, что  имеет простой делитель
длины не меньше
имеет простой делитель
длины не меньше  для некоторой константы для некоторой константы
 , , 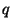 - из множества всех таких простых
делителей числа - из множества всех таких простых
делителей числа  , ,  -
из множества всех чисел -
из множества всех чисел  таких, что таких, что  , а , а
 . Тогда функция . Тогда функция
 -
односторонняя (см. главу 2). Рекомендации, данные
Шнорром относительно длин чисел -
односторонняя (см. главу 2). Рекомендации, данные
Шнорром относительно длин чисел 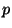 и и 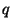 , можно трактовать
следующим образом. На тот момент (1989 г.)
инвертирование функции , можно трактовать
следующим образом. На тот момент (1989 г.)
инвертирование функции 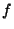 считалось практически
невыполнимым уже для
считалось практически
невыполнимым уже для 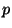 и и 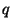 длины порядка 512 и 140
битов соответственно. Здесь, однако, следует учитывать, что
прогресс в области вычислительной техники и в
алгоритмической теории чисел (см. главу 4) может привести к
необходимости пересмотра этих величин. длины порядка 512 и 140
битов соответственно. Здесь, однако, следует учитывать, что
прогресс в области вычислительной техники и в
алгоритмической теории чисел (см. главу 4) может привести к
необходимости пересмотра этих величин.
В качестве секретного ключа схемы аутентификации Алиса
выбирает случайное число 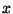 из из
 . Далее
Алиса вычисляет . Далее
Алиса вычисляет
 и публикует открытый ключ и публикует открытый ключ
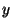 . Открытые
ключи всех участников схемы должны
публиковаться таким образом, чтобы исключалась возможность
их подмены (такое хранилище ключей называется
общедоступным сертифицированным справочником). Эта
проблема, называемая часто проблемой аутентичности открытых
ключей, составляет отдельный предмет исследований в
криптографии и в данной главе не рассматривается. . Открытые
ключи всех участников схемы должны
публиковаться таким образом, чтобы исключалась возможность
их подмены (такое хранилище ключей называется
общедоступным сертифицированным справочником). Эта
проблема, называемая часто проблемой аутентичности открытых
ключей, составляет отдельный предмет исследований в
криптографии и в данной главе не рассматривается.
Схема аутентификации Шнорра
Алиса выбирает случайное число  из множества из множества
 , вычисляет , вычисляет  и посылает и посылает  Бобу.
Бобу.
Боб выбирает случайный запрос  из множества из множества
 , где , где  - некоторый параметр, и
посылает - некоторый параметр, и
посылает  Алисе. Алисе.
Алиса вычисляет
 и посылает и посылает  Бобу. Бобу.
Боб проверяет соотношение
 и, если оно
выполняется, принимает доказательство, в противном случае
- отвергает. и, если оно
выполняется, принимает доказательство, в противном случае
- отвергает.
Отметим одно существенное отличие этого протокола от
протокола доказательства для задачи ИЗОМОРФИЗМ
ГРАФОВ, приведенного в главе 2: последний
протокол многораундовый, в нем количество раундов, т.е.
посылок сообщений от Алисы Бобу и обратно, возрастает с
ростом размерности задачи (количества вершин графа). А в
протоколе Шнорра количество раундов равно трем, вне
зависимости от значений других параметров. Поэтому с
практической точки зрения протокол Шнорра является
значительно более эффективным.
Первое
из требований к стойкости протоколов аутентификации,
корректность, означает, что противник, знающий
только открытый ключ 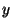 , может пройти аутентификацию лишь
с пренебрежимо малой вероятностью. Несложный анализ
показывает, что корректность протокола Шнорра зависит от
выбранного значения параметра , может пройти аутентификацию лишь
с пренебрежимо малой вероятностью. Несложный анализ
показывает, что корректность протокола Шнорра зависит от
выбранного значения параметра  . В самом деле, если . В самом деле, если  невелико, то противник имеет хорошие шансы просто угадать
тот запрос
невелико, то противник имеет хорошие шансы просто угадать
тот запрос  , который он получит от Боба на шаге 2.
Пусть для простоты , который он получит от Боба на шаге 2.
Пусть для простоты  . Тогда противник, не знающий
секретного ключа . Тогда противник, не знающий
секретного ключа 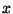 , может действовать следующим образом.
Подбросив монету, он выбирает равновероятным образом одно
из значений 0 или 1. Обозначим его через , может действовать следующим образом.
Подбросив монету, он выбирает равновероятным образом одно
из значений 0 или 1. Обозначим его через  . Далее
противник выбирает произвольное . Далее
противник выбирает произвольное  из из
 ,
вычисляет ,
вычисляет
 и посылает и посылает  Бобу. Ясно,
что запрос Бобу. Ясно,
что запрос  , полученный от Боба на шаге 2, совпадет с , полученный от Боба на шаге 2, совпадет с
 с вероятностью с вероятностью  , и именно с такой вероятностью
противник пройдет аутентификацию. , и именно с такой вероятностью
противник пройдет аутентификацию.
Если же значение  достаточно велико, то шансы угадать
запрос достаточно велико, то шансы угадать
запрос  малы. Шнорр [1] рекомендует малы. Шнорр [1] рекомендует  .
Разумеется, вероятность .
Разумеется, вероятность  , а именно такой будет
вероятность простого угадывания, можно считать пренебрежимо
малой. Но что будет, если противник атакует схему,
используя более изощренные методы? Задача теоретической
криптографии в том и состоит, чтобы исследовать стойкость
криптографических схем против любых (эффективных) атак
противника. , а именно такой будет
вероятность простого угадывания, можно считать пренебрежимо
малой. Но что будет, если противник атакует схему,
используя более изощренные методы? Задача теоретической
криптографии в том и состоит, чтобы исследовать стойкость
криптографических схем против любых (эффективных) атак
противника.
Если в схеме Шнорра Алиса является противником, то на шаге
1 вместо действий, предписанных протоколом, она может
выбирать  произвольным (но эффективным) образом. Иными
словами, Алиса использует некоторый полиномиальный
вероятностный алгоритм, который для каждого конкретного
значения произвольным (но эффективным) образом. Иными
словами, Алиса использует некоторый полиномиальный
вероятностный алгоритм, который для каждого конкретного
значения  определяет вероятность его выбора. определяет вероятность его выбора.
Пусть  - некоторое значение, которое Алиса передала
Бобу на шаге 1. Предположим, что нам удалось найти два
запроса - некоторое значение, которое Алиса передала
Бобу на шаге 1. Предположим, что нам удалось найти два
запроса
 , ,  ,
такие, что Алиса может для каждого из них найти
соответствующие значения ,
такие, что Алиса может для каждого из них найти
соответствующие значения  , для которых проверка на шаге
4 даст положительный результат. Обозначим эти значения , для которых проверка на шаге
4 даст положительный результат. Обозначим эти значения  через
через  и и  соответственно. Мы имеем: соответственно. Мы имеем:

Отсюда

или

Поскольку  , существует , существует
 и, следовательно,
и, следовательно,
 - дискретный
логарифм - дискретный
логарифм 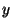 , т.е. , т.е.
 . .
Таким образом, либо запросы  , ,  , ,  ,
такие, что Алиса может ответить надлежащим образом на оба
из них (при одном и том же ,
такие, что Алиса может ответить надлежащим образом на оба
из них (при одном и том же  ) на шаге 3 протокола,
встречаются ``достаточно редко'', и это означает, что атака
Алисы успешна лишь с пренебрежимо малой вероятностью. Либо
такие значения попадаются ``достаточно часто'', и тогда тот
алгоритм, который применяет Алиса, можно использовать для
вычисления дискретных логарифмов. ) на шаге 3 протокола,
встречаются ``достаточно редко'', и это означает, что атака
Алисы успешна лишь с пренебрежимо малой вероятностью. Либо
такие значения попадаются ``достаточно часто'', и тогда тот
алгоритм, который применяет Алиса, можно использовать для
вычисления дискретных логарифмов.
Эта неформально изложенная идея была использована Шнорром
[1] для доказательства полиномиальной сводимости задачи
дискретного логарифмирования к задаче, стоящей перед
пассивным противником, т.е. таким, который пытается
пройти аутентификацию, зная лишь
открытый ключ. Иными
словами, доказано, что в предположении трудности задачи
дискретного логарифмирования схема аутентификации Шнорра
является стойкой против пассивного противника, т.е.
корректной.
Отметим, что вопреки весьма распространенному мнению, этот
результат, как и большинство подобных результатов в
теоретической криптографии, не является асимптотическим:
если задача дискретного логарифмирования трудна для чисел
(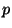 и и 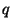 ) данной длины, то схема Шнорра является
корректной при использовании чисел той же длины. ) данной длины, то схема Шнорра является
корректной при использовании чисел той же длины.
Активный противник может провести некоторое количество
сеансов выполнения протокола в качестве проверяющего с
честным доказывающим (или подслушать такие выполнения) и
после этого попытаться атаковать схему аутентификации. Для
стойкости против активного противника достаточно, чтобы
протокол аутентификации был доказательством с нулевым
разглашением. Однако свойство нулевого разглашения для
схемы Шнорра до сих пор никому доказать не удалось. Более
того, на данный момент известен единственный метод
доказательства свойства нулевого разглашения - так
называемый метод ``черного ящика''. В этом методе
моделирующая машина использует алгоритм проверяющего
(машину Тьюринга  - в обозначениях из главы 2) лишь в
качестве оракула, т.е. не анализируя сам этот алгоритм,
подает ему на вход любые значения по своему выбору и
получает соответствующие выходные значения. Гольдрайх и
Кравчик доказали [2], что трехраундовые доказательства с
нулевым разглашением, в которых последнее свойство
устанавливается методом ``черного ящика'', существуют лишь в
тривиальном случае, т.е. когда проверяющий может
самостоятельно, без всякой помощи доказывающего, проверить
истинность утверждаемого. В отношении схемы Шнорра из этого
результата следует, что либо существует эффективный
алгоритм дискретного логарифмирования, либо свойство
нулевого разглашения этого протокола не может быть доказано
методом ``черного ящика''. Вопрос о существовании
доказательств с нулевым разглашением, для которых свойство
нулевого разглашения не может быть доказано методом
``черного ящика'', остается открытым. - в обозначениях из главы 2) лишь в
качестве оракула, т.е. не анализируя сам этот алгоритм,
подает ему на вход любые значения по своему выбору и
получает соответствующие выходные значения. Гольдрайх и
Кравчик доказали [2], что трехраундовые доказательства с
нулевым разглашением, в которых последнее свойство
устанавливается методом ``черного ящика'', существуют лишь в
тривиальном случае, т.е. когда проверяющий может
самостоятельно, без всякой помощи доказывающего, проверить
истинность утверждаемого. В отношении схемы Шнорра из этого
результата следует, что либо существует эффективный
алгоритм дискретного логарифмирования, либо свойство
нулевого разглашения этого протокола не может быть доказано
методом ``черного ящика''. Вопрос о существовании
доказательств с нулевым разглашением, для которых свойство
нулевого разглашения не может быть доказано методом
``черного ящика'', остается открытым.
Нетрудно показать, что схема Шнорра обладает несколько
более слабым свойством - свойством нулевого разглашения
относительно честного проверяющего. В этом случае
достаточно построить моделирующую машину только для
честного проверяющего, который на шаге 2 и в самом деле
выбирает случайный запрос  из множества из множества
 . .
Вся информация, которую получает Боб в результате
выполнения протокола - это тройка чисел  такая,
что такая,
что
 и и  . Обозначим множество
всех таких троек через . Обозначим множество
всех таких троек через  . В этой тройке число . В этой тройке число  выбирается случайным образом из
выбирается случайным образом из
 , а , а
 , где , где  - случайное число из множества - случайное число из множества
 . Ясно, что при таком выборе . Ясно, что при таком выборе  значение значение
 будет распределено равновероятным образом среди всех
отличных от единицы элементов группы, порожденной будет распределено равновероятным образом среди всех
отличных от единицы элементов группы, порожденной  .
Значение .
Значение  вычисляется согласно шагу 3 протокола и
определяется величинами вычисляется согласно шагу 3 протокола и
определяется величинами  и и  однозначно. Таким
образом, распределение вероятностей на множестве однозначно. Таким
образом, распределение вероятностей на множестве  определяется случайным выбором чисел
определяется случайным выбором чисел  и и  . .
Моделирующая машина должна создать на множестве  такое же распределение вероятностей как в протоколе. Но при
этом она не может использовать формулу из шага 3, поскольку
в нее входит секретный ключ
такое же распределение вероятностей как в протоколе. Но при
этом она не может использовать формулу из шага 3, поскольку
в нее входит секретный ключ 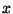 . Вместо этого моделирующая
машина выбирает случайные . Вместо этого моделирующая
машина выбирает случайные  и и  из из
 и и
 соответственно и вычисляет соответственно и вычисляет
 . Если . Если  , то попытка неудачна и
выбираются новые , то попытка неудачна и
выбираются новые  и и  . В противном случае моделирующая
машина выдает тройку . В противном случае моделирующая
машина выдает тройку  . Напомним, что моделирующая
машина строится только для честного доказывающего. Из
этого, в частности, следует, что открытый ключ . Напомним, что моделирующая
машина строится только для честного доказывающего. Из
этого, в частности, следует, что открытый ключ 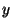 принадлежит группе, порожденной
принадлежит группе, порожденной  , т.е. существует
число , т.е. существует
число
 такое, что такое, что
 .
Поэтому при любых .
Поэтому при любых  и и  число число
 также принадлежит этой
группе.
Остается лишь заметить, что поскольку моделирующая машина
выбирает число также принадлежит этой
группе.
Остается лишь заметить, что поскольку моделирующая машина
выбирает число  случайным образом и независимо от
значения случайным образом и независимо от
значения  , величина , величина  - случайный элемент
множества - случайный элемент
множества
 , также не зависящий от , также не зависящий от  .
Поэтому число .
Поэтому число  , сгенерированное моделирующей машиной,
является случайным элементом группы, порожденной , сгенерированное моделирующей машиной,
является случайным элементом группы, порожденной  , не
зависящим от , не
зависящим от  , т.е. имеет такое же распределение, как в
протоколе. Иными словами, одно и то же распределение
вероятностей на множестве , т.е. имеет такое же распределение, как в
протоколе. Иными словами, одно и то же распределение
вероятностей на множестве  можно создать двумя
способами: либо выбрать случайное можно создать двумя
способами: либо выбрать случайное  (а, следовательно, и (а, следовательно, и
 ) и вычислить ) и вычислить
 , либо выбрать случайное , либо выбрать случайное  и получить
и получить
 . .
Свойства нулевого разглашения относительно честного
проверяющего может оказаться достаточно, если схема
аутентификации используется, например, для контроля за
доступом в охраняемое помещение. В этом случае Алиса -
это пропуск, выполненный в виде интеллектуальной карточки,
а Боб - компьютер охраны. В такой ситуации главная задача
- обеспечить корректность схемы аутентификации, а
защищаться от нечестного проверяющего бессмысленно. Что же
касается свойства нулевого разглашения относительно
честного проверяющего, то оно представляется далеко не
лишним, так как позволяет обезопаситься от противника,
который может попытаться подслушивать сеансы выполнения
протокола с целью изготовления фальшивого пропуска.
Пример протокола аутентификации приведен в эпиграфе к
данному разделу. В этом протоколе коза выступает в качестве
доказывающего, а семеро козлят - в качестве проверяющего.
Протокол призван обеспечивать целостность. В данном случае
- целостность семерых козлят. В эпиграфе описана и атака
на протокол. Противником выступает волк, и этот противник
активный: сначала он подслушивает выполнение протокола,
потом пытается сам пройти аутентификацию в качестве
доказывающего (козы) и при этом накапливает и анализирует
получаемую информацию. Протокол оказался нестойким против
активного противника. Надо было обратиться за консультацией
к профессиональным криптографам и использовать, например,
схему Шнорра.
Прежде чем завершить разговор о протоколах аутентификации
необходимо подчеркнуть, что никакое математически строго
доказанное свойство криптографического протокола не может
гарантировать его безопасности во всех случаях жизни. В
самом деле, даже протокол доказательства с нулевым
разглашением не защищает от следующей атаки на схему
аутентификации, известной в криптографической литературе
под названием ``мафиозная угроза''. В данном сценарии
имеются четыре участника:  , ,  , , 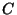 и и 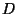 . Предположим,
что . Предположим,
что  зашел в кафе выпить чашечку кофе и расплачивается с
помощью кредитной карточки. Для выполнения любой банковской
операции карточка должна идентифицировать себя, т.е.
выполнить протокол аутентификации. Но владелец кафе, зашел в кафе выпить чашечку кофе и расплачивается с
помощью кредитной карточки. Для выполнения любой банковской
операции карточка должна идентифицировать себя, т.е.
выполнить протокол аутентификации. Но владелец кафе,  ,
- мафиози, сообщник которого ,
- мафиози, сообщник которого 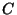 в тот же самый момент
находится в магазине ювелира в тот же самый момент
находится в магазине ювелира 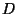 и пытается купить
бриллиант, также с помощью кредитной карточки. При этом и пытается купить
бриллиант, также с помощью кредитной карточки. При этом 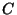 ``представляется'' как
``представляется'' как  , а , а 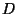 просит доказать это с
помощью протокола аутентификации. Устройство считывания для
карточек у просит доказать это с
помощью протокола аутентификации. Устройство считывания для
карточек у  и карточка у и карточка у 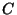 - это специально
изготовленные приемо-передающие устройства, которые лишь
пересылают сообщения между - это специально
изготовленные приемо-передающие устройства, которые лишь
пересылают сообщения между  и и 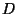 . В результате . В результате  ,
обмениваясь сообщениями с ,
обмениваясь сообщениями с  , на самом деле идентифицирует
себя для , на самом деле идентифицирует
себя для 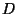 . .
Мы здесь не затрагиваем вопроса о практической
осуществимости ``мафиозной угрозы''. Мы привели ее просто
как пример, показывающий, что только математического обоснования
стойкости того или иного криптографического протокола
недостаточно. Для практического применения
конкретного протокола требуются еще усилия специалистов в
области информационной безопасности по анализу условий его
применения.
Теперь мы переходим к обсуждению другого типа протоколов
аутентификации - к протоколам электронной подписи.
Они
обеспечивают аутентификацию сообщений, т.е. гарантируют,
что сообщения поступают от достоверного отправителя и в
неискаженном виде. Более того, целостность здесь
понимается в расширенном смысле: получатель сообщения не
только убеждается в его достоверности, но и получает
электронную подпись, которую в дальнейшем может
использовать как доказательство достоверности сообщения
третьим лицам (арбитру) в том случае, если отправитель
впоследствии попытается отказаться от своей подписи. Здесь
имеется полная аналогия обычной подписи на бумаге, за
исключением того, что под арбитром обычно понимается
технический эксперт, который дает заключение о подлинности
электронной подписи, т.е. выполняет функцию, аналогичную
функции графолога в случае обычной подписи. Назначение схем
электронной подписи мы уже обсуждали во введении на примере
платежных поручений.
Все протоколы электронной подписи, разрабатываемые для
практического применения, являются неинтерактивными (т.е.
весь обмен сообщениями состоит в передаче отправителем
получателю подписанного сообщения). Это вызвано, прежде
всего, требованиями к эффективности.
Как обычно, математическая формализация рассматривает схему
электронной подписи как бесконечное семейство схем,
зависящих от целочисленного параметра  , ,  ,
называемого параметром безопасности. ,
называемого параметром безопасности.
Схема электронной подписи - это тройка алгоритмов
 , где , где
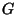 - полиномиальный вероятностный алгоритм генерации
ключей. На входе - полиномиальный вероятностный алгоритм генерации
ключей. На входе  алгоритм алгоритм 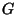 выдает пару выдает пару
 , где , где 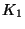 - открытый ключ схемы подписи, а - открытый ключ схемы подписи, а
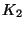 - соответствующий ему секретный ключ. Ключ - соответствующий ему секретный ключ. Ключ 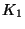 помещается в общедоступный сертифицированный справочник;
помещается в общедоступный сертифицированный справочник;
 - полиномиальный вероятностный алгоритм генерации
подписей. На входе - полиномиальный вероятностный алгоритм генерации
подписей. На входе  , где , где  - сообщение,
алгоритм - сообщение,
алгоритм  выдает подпись выдает подпись  для сообщения для сообщения  ; ;
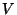 - полиномиальный алгоритм проверки подписи. Если - полиномиальный алгоритм проверки подписи. Если
 , то подпись , то подпись  для сообщения для сообщения  принимается. В этом случае говорят, что
принимается. В этом случае говорят, что  - корректная
подпись для сообщения - корректная
подпись для сообщения  . Если . Если
 , то подпись , то подпись
 отвергается. Если подпись отвергается. Если подпись  для сообщения для сообщения  сгенерирована на ключе сгенерирована на ключе
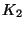 с помощью алгоритма с помощью алгоритма  , то всегда должно быть , то всегда должно быть
 . .
Здесь 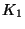 , , 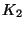 , ,  и и  - двоичные
строки, длины которых ограничены некоторыми фиксированными
полиномами от - двоичные
строки, длины которых ограничены некоторыми фиксированными
полиномами от  . .
Для определения стойкости схемы электронной подписи
необходимо принять некоторые предположения о противнике.
Последний может пытаться подделывать подписи, зная только
открытый ключ схемы.
Такой противник называется пассивным и
является самым слабым из всех возможных противников, так как
открытый ключ схемы подписи всегда общедоступен.
Разумеется, пассивный противник, как и любой другой, знает
описание схемы подписи, поскольку предполагается, что
алгоритмы 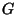 , ,  и и 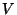 общедоступны. общедоступны.
Более изобретательный противник может попытаться собрать
некоторую дополнительную информацию о схеме подписи, набрав
некоторое количество пар (сообщение, подпись). Здесь
имеются два основных варианта.
Атака с известными
сообщениями состоит в том, что противник перехватывает
некоторое (ограниченное фиксированным полиномом от  )
количество подписанных сообщений. При этом противник никак
не влияет на выбор этих сообщений. По существу это -
разновидность пассивного противника, так как подписанные
сообщения обычно пересылаются по общедоступному каналу
связи (в некоторых работах по теоретической криптографии
принимается математическая модель, в которой подписанные
сообщения просто публикуются). )
количество подписанных сообщений. При этом противник никак
не влияет на выбор этих сообщений. По существу это -
разновидность пассивного противника, так как подписанные
сообщения обычно пересылаются по общедоступному каналу
связи (в некоторых работах по теоретической криптографии
принимается математическая модель, в которой подписанные
сообщения просто публикуются).
Еще более сильный противник может сам выбирать сообщения и
каким-то образом получать корректные подписи для них. Такая
атака называется атакой с выбором сообщений, а
соответствующий противник - активным. Вопрос о
практической осуществимости подобной атаки выходит за рамки
математической модели и в данной главе не рассматривается.
Отметим лишь, что, по-видимому, никакими организационными
мерами нельзя полностью исключить возможность атаки с
выбором сообщений и здесь, как и всюду в теоретической
криптографии, делается предположение в пользу противника.
Это значит, что обычно
исследуется стойкость схем электронной подписи в
присутствии самого сильного противника, осуществляющего
атаку с выбором сообщений.
Помимо атаки необходимо также определить ту угрозу
безопасности схемы электронной подписи, против которой мы
желаем защищаться. Самая сильная угроза - полное
раскрытие, т.е.
вычисление противником секретного ключа
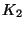 . Ясно, что если противник может осуществить подобную
угрозу, то схема нестойкая. С другой стороны, нетрудно
понять, что стойкости против полного раскрытия недостаточно
для того, чтобы считать схему подписи стойкой на практике.
Достаточно рассмотреть следующую вырожденную схему.
Алгоритм . Ясно, что если противник может осуществить подобную
угрозу, то схема нестойкая. С другой стороны, нетрудно
понять, что стойкости против полного раскрытия недостаточно
для того, чтобы считать схему подписи стойкой на практике.
Достаточно рассмотреть следующую вырожденную схему.
Алгоритм 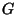 выбирает случайный секретный ключ выбирает случайный секретный ключ 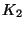 и
вычисляет и
вычисляет  , где , где 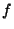 - некоторая односторонняя
функция. Подпись для сообщения - некоторая односторонняя
функция. Подпись для сообщения  алгоритм алгоритм  вычисляет в
виде вычисляет в
виде  , где , где  - некоторая легко вычислимая
функция. Функция - некоторая легко вычислимая
функция. Функция  публикуется как часть открытого ключа, и проверка
подписи состоит в вычислении публикуется как часть открытого ключа, и проверка
подписи состоит в вычислении  и сравнении подписи и сравнении подписи  с этим
значением. Ясно, что такая схема будет стойкой против полного
раскрытия, поскольку для вычисления секретного ключа с этим
значением. Ясно, что такая схема будет стойкой против полного
раскрытия, поскольку для вычисления секретного ключа 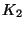 требуется
инвертировать одностороннюю функцию требуется
инвертировать одностороннюю функцию 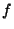 . Но всякий желающий может
вычислить подпись для любого сообщения. Этот пример поучителен еще и
потому, что в криптографической литературе встречаются статьи, в
которых анализ стойкости схем электронной подписи подменяется
рассуждениями о сложности задачи полного раскрытия. . Но всякий желающий может
вычислить подпись для любого сообщения. Этот пример поучителен еще и
потому, что в криптографической литературе встречаются статьи, в
которых анализ стойкости схем электронной подписи подменяется
рассуждениями о сложности задачи полного раскрытия.
На другом полюсе находится самая слабая из угроз -
угроза
экзистенцианальной подделки. Такая угроза
осуществима, если после проведения атаки на схему
электронной подписи противник может подделать подпись хотя
бы для одного, пусть даже бессмысленного, сообщения.
Стойкость схемы электронной подписи определяется
относительно пары (атака, угроза). Наиболее стойкими
являются схемы, стойкие против самой слабой из угроз на
основе самой сильной из атак, т.е. против
экзистенцианальной подделки на основе атаки с выбором
сообщений. Опишем эти атаку и угрозу на несколько более
строгом уровне. Систематическое изложение атак и угроз для
схем электронной подписи см. в [3].
Под противником мы понимаем вероятностную машину
Тьюринга  , которая получает на входе , которая получает на входе  и и 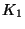 и
завершает свою работу за полиномиальное (от и
завершает свою работу за полиномиальное (от  ) время.
Машина ) время.
Машина  имеет доступ к алгоритму имеет доступ к алгоритму  генерации подписей
(знающему секретный ключ генерации подписей
(знающему секретный ключ 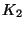 ) как к оракулу. Тем самым ) как к оракулу. Тем самым  может выбрать сообщения
может выбрать сообщения
 , где , где  для некоторого полинома
для некоторого полинома 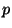 , и получить для них корректные
подписи , и получить для них корректные
подписи
 соответственно. При оценке
времени работы машины соответственно. При оценке
времени работы машины  каждое обращение к оракулу
считается одной командой. Можно считать, что к моменту
выбора сообщения каждое обращение к оракулу
считается одной командой. Можно считать, что к моменту
выбора сообщения  машина машина  уже знает подписи уже знает подписи
 для всех предшествующих сообщений.
Такая атака называется адаптивной. После этого машина для всех предшествующих сообщений.
Такая атака называется адаптивной. После этого машина  должна найти пару
должна найти пару  , где , где  для всех для всех
 такую, что такую, что  - корректная подпись для
сообщения - корректная подпись для
сообщения  . Обозначим через . Обозначим через
 событие, состоящее в том, что событие, состоящее в том, что  находит такую
пару. Схема электронной подписи находит такую
пару. Схема электронной подписи  называется
стойкой против экзистенцианальной подделки на основе
(адаптивной) атаки с выбором сообщений, если для любой
машины Тьюринга называется
стойкой против экзистенцианальной подделки на основе
(адаптивной) атаки с выбором сообщений, если для любой
машины Тьюринга  указанного выше вида, для любого
полинома указанного выше вида, для любого
полинома 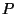 и для всех достаточно больших и для всех достаточно больших 

Вероятность
здесь определяется случайными величинами алгоритмов 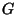 , ,
 и и  . .
Несложные рассуждения, аналогичные тем, которые приведены в
главе 2, показывают, что для существования схем электронной
подписи, стойких против экзистенцианальной подделки на
основе атаки с выбором сообщений, необходимо существование
односторонних функций. Одно из замечательных достижений
теоретической криптографии состоит в доказательстве того,
что это условие одновременно является и достаточным.
Поскольку этот результат весьма нетривиален, ниже мы лишь
схематично излагаем основные идеи.
Рассмотрим вначале схему электронной подписи Лампорта[4].
Пусть
 , где , где
 , - односторонняя функция и пусть , - односторонняя функция и пусть  -
множество, из которого выбираются подписываемые сообщения
(т.е. каждое сообщение -
множество, из которого выбираются подписываемые сообщения
(т.е. каждое сообщение
 рассматривается
как рассматривается
как  -битовая строка).
Алгоритм вычисления функции -битовая строка).
Алгоритм вычисления функции 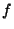 считается общедоступным. считается общедоступным.
Алгоритм генерации ключей выбирает  случайных строк
из случайных строк
из 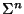 : :
 .
Совокупность этих .
Совокупность этих  строк составляет
секретный ключ схемы подписи. Далее алгоритм вычисляет строк составляет
секретный ключ схемы подписи. Далее алгоритм вычисляет

Совокупность строк
 публикуется как открытый ключ
схемы. публикуется как открытый ключ
схемы.
Подписью для сообщения
 служит
последовательность строк служит
последовательность строк
 . Иными словами, для . Иными словами, для 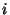 -го бита сообщения -го бита сообщения  открывается одно из значений
открывается одно из значений  или или  в
зависимости от того, чему равен в
зависимости от того, чему равен 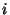 -ый бит -ый бит  - нулю
или единице. Проверка подписи - нулю
или единице. Проверка подписи
 очевидна: для каждого
очевидна: для каждого  вычисляется значение вычисляется значение
 и сравнивается с соответствующей строкой и сравнивается с соответствующей строкой
 из открытого ключа. из открытого ключа.
Схема Лампорта ``одноразовая'', она позволяет подписать одно
 -битовое сообщение, после чего надо сгенерировать новые
ключи и заменить открытый ключ в сертифицированном
справочнике. Но с другой стороны, эта схема уже обладает
тем свойством, которого мы добиваемся: если -битовое сообщение, после чего надо сгенерировать новые
ключи и заменить открытый ключ в сертифицированном
справочнике. Но с другой стороны, эта схема уже обладает
тем свойством, которого мы добиваемся: если 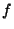 -
односторонняя функция, то схема стойкая. В самом деле,
пусть -
односторонняя функция, то схема стойкая. В самом деле,
пусть
 - открытый
ключ, а - открытый
ключ, а  - сообщение и корректная подпись для него,
вычисленная на секретном ключе - сообщение и корректная подпись для него,
вычисленная на секретном ключе
 ,
соответствующем открытому ключу ,
соответствующем открытому ключу 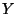 .
Предположим, что противник может за полиномиальное время с
вероятностью по крайней мере .
Предположим, что противник может за полиномиальное время с
вероятностью по крайней мере  для некоторого
полинома для некоторого
полинома 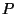 найти пару найти пару  , где , где  ,
а ,
а  - корректная подпись для - корректная подпись для  . Пусть . Пусть  -
номер бита, в котором отличаются сообщения -
номер бита, в котором отличаются сообщения  и и
 , и предположим для определенности, что , и предположим для определенности, что
 , а , а  . Тогда в подписи . Тогда в подписи  отсутствует значение
отсутствует значение  , а в , а в  должно
присутствовать какое-либо значение должно
присутствовать какое-либо значение 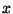 такое, что такое, что
 .
Следовательно, алгоритм .
Следовательно, алгоритм  , которым пользуется противник
для вычисления , которым пользуется противник
для вычисления  , должен уметь инвертировать функцию , должен уметь инвертировать функцию 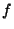 на этом значении
на этом значении  . Тогда следующий алгоритм
будет противоречить предположению о том, что функция . Тогда следующий алгоритм
будет противоречить предположению о том, что функция 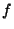 односторонняя. Пусть
односторонняя. Пусть  выбрано наудачу из выбрано наудачу из 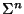 и и
 задано нам в качестве входного значения. Выбираем
случайное задано нам в качестве входного значения. Выбираем
случайное 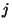 из множества из множества
 . Для всех . Для всех
 , ,  , генерируем соответствующие
компоненты ключей , генерируем соответствующие
компоненты ключей  и и 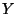 с помощью алгоритма с помощью алгоритма 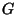 , а
вместо , а
вместо 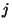 -го элемента ключа -го элемента ключа 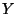 подставляем подставляем  . Далее
вызываем алгоритм . Далее
вызываем алгоритм  , подавая ему на вход ключ , подавая ему на вход ключ 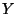 . Когда . Когда
 запросит подпись для некоторого сообщения запросит подпись для некоторого сообщения  ,
проверяем, требуется ли для подписания этого сообщения
прообраз значения ,
проверяем, требуется ли для подписания этого сообщения
прообраз значения  . Если да, то попытка неудачна
(вероятность этого . Если да, то попытка неудачна
(вероятность этого  ). В
противном случае создаем подпись ). В
противном случае создаем подпись  для для  и передаем ее
алгоритму и передаем ее
алгоритму  . .
Если  успешно подделывает подпись для некоторого
сообщения успешно подделывает подпись для некоторого
сообщения  , ,  , то проверяем, не содержит ли
эта подпись прообраз значения , то проверяем, не содержит ли
эта подпись прообраз значения  . Если да, то выдаем этот
прообраз. . Если да, то выдаем этот
прообраз.
Ясно, что в случае успеха описанный алгоритм инвертирует
функцию 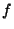 . Очевидно также, что этот алгоритм работает за
полиномиальное время. Оценим теперь вероятность успеха.
Прежде всего заметим, что алгоритм . Очевидно также, что этот алгоритм работает за
полиномиальное время. Оценим теперь вероятность успеха.
Прежде всего заметим, что алгоритм  получает на вход
только открытый ключ получает на вход
только открытый ключ 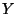 и распределение вероятностей на
множестве всех возможных значений и распределение вероятностей на
множестве всех возможных значений 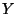 такое же как в том
случае, когда такое же как в том
случае, когда  атакует схему подписи. Поэтому мы угадаем атакует схему подписи. Поэтому мы угадаем
 и и  (т.е. произойдет событие (т.е. произойдет событие
 ) с вероятностью ) с вероятностью  . Общая вероятность
успеха будет по крайней мере . Общая вероятность
успеха будет по крайней мере
 ,
что не меньше, чем ,
что не меньше, чем  для некоторого
полинома для некоторого
полинома  (напомним, что по определению (напомним, что по определению  не
превосходит некоторого полинома от параметра безопасности не
превосходит некоторого полинома от параметра безопасности
 ). ).
В качестве своеобразного криптографического курьеза укажем,
что если в схеме Лампорта разрешить подписывать любые
сообщения, длина которых не превосходит  , то из подписи
для сообщения , то из подписи
для сообщения  можно легко создать подпись для любого
его префикса. Например, из подписи для сообщения,
представляющего собой знаменитую фразу ``казнить нельзя,
помиловать'' можно изготовить подпись для сообщения
``казнить''. Конечно, в данном случае можно предложить
простые и эффективные контрмеры. Например, можно
потребовать, чтобы короткие сообщения дополнялись справа
двоичными нулями до длины можно легко создать подпись для любого
его префикса. Например, из подписи для сообщения,
представляющего собой знаменитую фразу ``казнить нельзя,
помиловать'' можно изготовить подпись для сообщения
``казнить''. Конечно, в данном случае можно предложить
простые и эффективные контрмеры. Например, можно
потребовать, чтобы короткие сообщения дополнялись справа
двоичными нулями до длины  . Но этот курьез служит
хорошей иллюстрацией следующего общего принципа: всякое
утверждение о стойкости какой-либо криптографической схемы
требует точной спецификации значений всех ее параметров и
зачастую даже незначительное отступление от установленных
значений полностью разрушает стойкость схемы. . Но этот курьез служит
хорошей иллюстрацией следующего общего принципа: всякое
утверждение о стойкости какой-либо криптографической схемы
требует точной спецификации значений всех ее параметров и
зачастую даже незначительное отступление от установленных
значений полностью разрушает стойкость схемы.
Теперь осталось только преобразовать схему Лампорта в
``многоразовую''. Идея такого преобразования достаточно
очевидна: в момент подписания очередного сообщения  нужно выбрать новые секретный и открытый ключи
нужно выбрать новые секретный и открытый ключи  и и 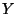 и
отправить получателю тройку и
отправить получателю тройку  , где , где  -
подпись для сообщения -
подпись для сообщения  . В результате возникает
цепочка открытых ключей . В результате возникает
цепочка открытых ключей
 и
соответствующих им подписей и
соответствующих им подписей
 .
Здесь .
Здесь  - открытый ключ, хранящийся в
сертифицированном справочнике, а - открытый ключ, хранящийся в
сертифицированном справочнике, а  - подпись для
ключа - подпись для
ключа  , сгенерированная с помощью секретного ключа , сгенерированная с помощью секретного ключа
 , соответствующего открытому ключу , соответствующего открытому ключу  .
Таким образом, каждый открытый ключ .
Таким образом, каждый открытый ключ  будет
аутентифицирован посредством цепочки подписей будет
аутентифицирован посредством цепочки подписей
 и, следовательно, может использоваться совместно с
секретным ключом и, следовательно, может использоваться совместно с
секретным ключом  для генерации и проверки подписей
для сообщений. Проблема, однако, в том, что с помощью одной
пары ключей для генерации и проверки подписей
для сообщений. Проблема, однако, в том, что с помощью одной
пары ключей  можно подписать только можно подписать только  битов
сообщения, а длина одного только нового открытого ключа
равна битов
сообщения, а длина одного только нового открытого ключа
равна  битам. битам.
Для описания способа решения этой проблемы нам потребуется
новое понятие - понятие криптографической хэш-функции.
Хэш-функции - весьма любопытный криптографический
примитив, заслуживающий отдельного разговора. Здесь же мы
лишь кратко обсудим это понятие. Говоря неформально,
криптографическая хэш-функция -
это легко вычислимая
функция, сжимающая входные значения, для которой не
существует эффективного алгоритма поиска коллизий.
Коллизией для функции
 называется пара значений называется пара значений 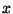 , ,
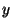 , ,  , такая, что , такая, что  . Поскольку
хэш-функция сжимает входные значения, коллизии заведомо
существуют и их можно найти полным перебором. Но,
по определению, никакой
полиномиальный алгоритм не найдет коллизий у криптографической
хэш-функции. . Поскольку
хэш-функция сжимает входные значения, коллизии заведомо
существуют и их можно найти полным перебором. Но,
по определению, никакой
полиномиальный алгоритм не найдет коллизий у криптографической
хэш-функции.
Следующее определение семейства
односторонних хэш-функций было дано Наором и Юнгом [4].
Пусть  - целочисленный параметр, - целочисленный параметр,  и и  -
множество функций -
множество функций
 , где , где
 . При этом предполагается, что . При этом предполагается, что
 для некоторого полинома для некоторого полинома 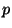 . Далее, каждая
функция . Далее, каждая
функция  имеет описание имеет описание  и существует
полиномиальный вероятностный алгоритм, который на входе и существует
полиномиальный вероятностный алгоритм, который на входе
 выбирает равновероятным образом из множества всех
описаний функций из выбирает равновероятным образом из множества всех
описаний функций из  . Предполагается также, что
существует полиномиальный алгоритм, который, получив на
вход описание . Предполагается также, что
существует полиномиальный алгоритм, который, получив на
вход описание  функции из функции из  и и
 ,
выдает значение ,
выдает значение  . Под противником, который пытается
отыскать коллизии, понимается полиномиальный вероятностный
алгоритм . Под противником, который пытается
отыскать коллизии, понимается полиномиальный вероятностный
алгоритм  , работающий в два этапа. Сначала он получает
на вход , работающий в два этапа. Сначала он получает
на вход  и должен выдать какое-нибудь значение и должен выдать какое-нибудь значение 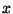 из из
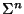 . После этого . После этого  получает получает  , выбранное
наудачу из множества всех описаний функций из , выбранное
наудачу из множества всех описаний функций из  .
Семейство .
Семейство  называется семейством односторонних
хэш-функций, если для любого такого алгоритма называется семейством односторонних
хэш-функций, если для любого такого алгоритма  , для
любого полинома , для
любого полинома 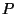 и для всех достаточно больших и для всех достаточно больших 

Предположим, что существует семейство односторонних
хэш-функций  , где , где
 . Как показали
Наор и Юнг [4], с помощью такого семейства схему Лампорта можно превратить в
``многоразовую'' следующим образом. Подписывающий выбирает
случайное описание . Как показали
Наор и Юнг [4], с помощью такого семейства схему Лампорта можно превратить в
``многоразовую'' следующим образом. Подписывающий выбирает
случайное описание  функции функции  и
помещает это описание в сертифицированный справочник вместе
с открытым ключом и
помещает это описание в сертифицированный справочник вместе
с открытым ключом  . Подписываемые сообщения имеют
длину . Подписываемые сообщения имеют
длину  . Когда подписывается первое сообщение,
генерируется новая пара ключей . Когда подписывается первое сообщение,
генерируется новая пара ключей  и вычисляется
значение и вычисляется
значение  . Далее, с помощью первых . Далее, с помощью первых  элементов
ключа элементов
ключа  подписывается сообщение, а с помощью последних подписывается сообщение, а с помощью последних
 элементов - значение элементов - значение  . После этого сообщение,
новый открытый ключ . После этого сообщение,
новый открытый ключ  и подписи посылаются получателю.
Аналогичным образом подписываются все последующие
сообщения. Для проверки подписи нужно либо проверять всю
цепочку, начиная с и подписи посылаются получателю.
Аналогичным образом подписываются все последующие
сообщения. Для проверки подписи нужно либо проверять всю
цепочку, начиная с  , либо помнить последний
аутентифицированный подписывающим открытый ключ. , либо помнить последний
аутентифицированный подписывающим открытый ключ.
Анализ этой схемы (подробности см. в [4]) показывает, что
для подделки подписей противник должен уметь либо подменять
открытый ключ  , не меняя значения , не меняя значения  , а
значит, находить коллизии для функции , а
значит, находить коллизии для функции  , либо
инвертировать функцию , либо
инвертировать функцию 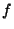 . .
Остается еще понять, почему указанная возможность находить
коллизии противоречит определению семейства односторонних
хэш-функций. Ведь противник заранее знает описание  и только потом получает значение, для которого требуется
найти коллизию; а значит, задача противника при атаке на схему
подписи кажется более легкой, чем та, которая указана в
определении семейства односторонних хэш-функций. Но дело в
том, что подписывающий выбирает и только потом получает значение, для которого требуется
найти коллизию; а значит, задача противника при атаке на схему
подписи кажется более легкой, чем та, которая указана в
определении семейства односторонних хэш-функций. Но дело в
том, что подписывающий выбирает  и все и все  равновероятным образом и независимо друг от друга.
Следовательно, и все
равновероятным образом и независимо друг от друга.
Следовательно, и все  будут независимы от будут независимы от  .
Поэтому противник, атакующий хэш-функцию, может сам выбрать
значение .
Поэтому противник, атакующий хэш-функцию, может сам выбрать
значение 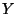 таким же образом, как это делает подписывающий,
и после этого получить случайное описание таким же образом, как это делает подписывающий,
и после этого получить случайное описание  . Легко
понять, что вероятность успеха атаки при этом не изменится. . Легко
понять, что вероятность успеха атаки при этом не изменится.
Наор и Юнг [4] построили семейство односторонних
хэш-функций, исходя из предположения о существовании
односторонней перестановки. Ромпель [5] усилил этот
результат, доказав, что достаточно (любой) односторонней
функции. Тем самым установлено, что схемы электронной
подписи, стойкие против экзистенцианальной подделки на
основе атаки с выбором сообщений, существуют тогда и только
тогда, когда существуют односторонние функции.
Этот фундаментальный результат можно интерпретировать
следующим образом. Если существуют схемы подписи, стойкие в
каком-либо, даже весьма слабом, смысле, то существуют и
схемы, стойкие против экзистенцианальной подделки на основе
атаки с выбором сообщений, т.е. схемы, стойкие в самом
сильном смысле. В самом деле, как уже
отмечалось выше, если
схему подписи можно считать в каком-либо смысле стойкой, то
она должна быть стойкой против полного раскрытия, а из
этого уже следует существование односторонних функций.
К сожалению, эта схема подписи слишком неэффективна, чтобы
ее можно было использовать на практике. Во-первых, подписи
имеют слишком большую длину. На каждый подписываемый бит
требуется  битов подписи. Во-вторых, получатель должен
хранить всю цепочку открытых ключей, начиная с битов подписи. Во-вторых, получатель должен
хранить всю цепочку открытых ключей, начиная с  , и всю
последовательность подписанных сообщений для предъявления
их арбитру в случае возникновения споров о подлинности
подписей. С помощью некоторых ухищрений можно несколько
сократить длины цепочек и уменьшить размер подписи, но
полностью избавиться от этих недостатков не удается. Вопрос
о возможности построения практически эффективных схем
электронной подписи, исходя из одного только предположения
о существования односторонней функции, остается открытым. , и всю
последовательность подписанных сообщений для предъявления
их арбитру в случае возникновения споров о подлинности
подписей. С помощью некоторых ухищрений можно несколько
сократить длины цепочек и уменьшить размер подписи, но
полностью избавиться от этих недостатков не удается. Вопрос
о возможности построения практически эффективных схем
электронной подписи, исходя из одного только предположения
о существования односторонней функции, остается открытым.
Рассмотрим теперь пример практической схемы электронной
подписи. Вернемся к схеме аутентификации Шнорра. В этом
протоколе интерактивность требуется только для того, чтобы
получить от проверяющего случайный запрос  . Поэтому
если бы у доказывающего был надежный источник случайности,
пользующийся доверием проверяющего, то протокол можно было
бы сделать неинтерактивным. Фиат и Шамир [6] предложили
способ
преобразования протокола аутентификации в схему электронной
подписи путем
замены случайного запроса неким ``суррогатом''.
А именно, пусть . Поэтому
если бы у доказывающего был надежный источник случайности,
пользующийся доверием проверяющего, то протокол можно было
бы сделать неинтерактивным. Фиат и Шамир [6] предложили
способ
преобразования протокола аутентификации в схему электронной
подписи путем
замены случайного запроса неким ``суррогатом''.
А именно, пусть  - подписываемое сообщение и - подписываемое сообщение и
 - криптографическая хэш-функция. Тогда вместо
обращения к проверяющему (он же - получатель сообщения)
доказывающий (он же - подписывающий) вычисляет величину - криптографическая хэш-функция. Тогда вместо
обращения к проверяющему (он же - получатель сообщения)
доказывающий (он же - подписывающий) вычисляет величину
 и использует ее в качестве запроса и использует ее в качестве запроса  . Этот метод
универсален, так как применим к широкому классу протоколов
аутентификации. Опишем теперь получаемую в результате
такого преобразования схему электронной подписи Шнорра [1].
Открытый и секретный ключи подписывающего генерируются в
этой схеме таким же образом, как в схеме аутентификации
Шнорра. Открытый ключ помещается в общедоступный
сертифицированный справочник. . Этот метод
универсален, так как применим к широкому классу протоколов
аутентификации. Опишем теперь получаемую в результате
такого преобразования схему электронной подписи Шнорра [1].
Открытый и секретный ключи подписывающего генерируются в
этой схеме таким же образом, как в схеме аутентификации
Шнорра. Открытый ключ помещается в общедоступный
сертифицированный справочник.
Схема
электронной подписи Шнорра
Подписывающий выбирает случайное число
 и вычисляет и вычисляет  . .
Подписывающий вычисляет  , где , где  -
подписываемое сообщение. -
подписываемое сообщение.
Подписывающий вычисляет
 и посылает
сообщение и посылает
сообщение  с подписью с подписью  получателю. получателю.
Получатель вычисляет
 и проверяет,
выполняется ли равенство и проверяет,
выполняется ли равенство  . Если да, то подпись
принимается, в противном случае - отвергается. . Если да, то подпись
принимается, в противном случае - отвергается.
Предполагается, что хэш-функция  отображает пары
значений отображает пары
значений  в множество в множество
 . .
Легко проверить, что для подписи, сгенерированной согласно
протоколу, проверка п.4 всегда будет выполнена.
Стойкость схемы Шнорра в значительной степени зависит
от свойств функции  . Если противник умеет отыскивать
коллизии специального вида, т.е. по заданной паре . Если противник умеет отыскивать
коллизии специального вида, т.е. по заданной паре  находить
другое сообщение находить
другое сообщение  , ,  , такое, что , такое, что
 , то он
может осуществлять экзистенцианальную подделку подписей. Для этого
достаточно перехватить сообщение , то он
может осуществлять экзистенцианальную подделку подписей. Для этого
достаточно перехватить сообщение  и подпись и подпись  для него, а
также найти коллизию указанного вида. Тогда пара для него, а
также найти коллизию указанного вида. Тогда пара  будет также подписью и для сообщения
будет также подписью и для сообщения  . .
Хэш-функции являются неотъемлемой частью конструкции схем
электронной подписи. Это является следствием необходимости
подписывать сообщения различной длины. Конечно, длинные
сообщения можно разбивать на блоки, имеющие требуемую для
схемы подписи длину, и подписывать каждый блок. Но это
решение неэффективно. На практике используются хэш-функции,
которые преобразуют сообщения произвольной длины в
хэш-значения требуемой длины. Ясно, что такая хэш-функция
должна быть в каком-то смысле стойкой против попыток найти
коллизии. Но поскольку практические хэш-функции
конструируются для конкретных длин хэш-значений (скажем,
256 битов), формализовать это требование не удается.
В отличие от протоколов аутентификации, для практических
схем электронной подписи не известно методов доказательства
стойкости. Стойкие схемы подписи не могут быть
доказательствами с нулевым разглашением. Это легко понять,
если вспомнить, что определение нулевого разглашения
требует существования моделирующей машины, которая, не зная
секретного ключа, создает для всех величин, наблюдаемых
проверяющим, распределение вероятностей, неотличимое от
того, которое возникает при выполнении протокола. Но все,
что видит проверяющий (он же - получатель) в процессе
выполнения протокола, это - сообщения с подписями.
Следовательно, моделирующая машина, если она существует,
может подделывать подписи, так как создаваемые ею ``подписи''
должны быть неотличимы от подлинных, в частности, и для
алгоритма проверки подписей.
Стойкость схем электронной подписи против пассивного
противника, который, зная только открытый ключ, пытается
подделывать подписи, может быть доказана в так называемой
модели со случайным оракулом. В
этой модели подписывающий и
проверяющий вместо вычисления функции  обращаются к
оракулу, который для каждого входного значения обращаются к
оракулу, который для каждого входного значения  выбирает случайное выходное значение
выбирает случайное выходное значение  и выдает его в
качестве ответа. При этом пара и выдает его в
качестве ответа. При этом пара
 запоминается и в случае повторного обращения с входным
значением
запоминается и в случае повторного обращения с входным
значением  оракул снова выдаст значение оракул снова выдаст значение  .
Как заметили Фиат и Шамир [6], изложенная выше идея
доказательства корректности схем аутентификации применима в
данной модели для доказательства стойкости схем подписи
против
пассивного
противника. Этот результат справедлив для
широкого класса схем подписи, включающего схему Шнорра.
Фактически это означает, что схемы подписи являются
стойкими (против указанного выше пассивного противника),
если хэш-функция ведет себя, как случайная функция. Это
утверждение является по-существу единственным результатом
теоретической криптографии, касающимся стойкости
практических схем электронной подписи, если не считать
работы [8], где то же самое доказано в предположении, что
хэш-функция ведет себя, как функция дешифрования стойкой, в
некотором смысле, криптосистемы. .
Как заметили Фиат и Шамир [6], изложенная выше идея
доказательства корректности схем аутентификации применима в
данной модели для доказательства стойкости схем подписи
против
пассивного
противника. Этот результат справедлив для
широкого класса схем подписи, включающего схему Шнорра.
Фактически это означает, что схемы подписи являются
стойкими (против указанного выше пассивного противника),
если хэш-функция ведет себя, как случайная функция. Это
утверждение является по-существу единственным результатом
теоретической криптографии, касающимся стойкости
практических схем электронной подписи, если не считать
работы [8], где то же самое доказано в предположении, что
хэш-функция ведет себя, как функция дешифрования стойкой, в
некотором смысле, криптосистемы.
Next: 3.3. Неотслеживаемость. Электронные деньги
Up: 3. Криптографические протоколы
Previous: 3.1. Введение
Contents: Содержание
|

