Next: Задачи второй олимпиады
Up: 7.5. Условия задач олимпиад
Previous: 7.5. Условия задач олимпиад
Contents: Содержание
1.1. Ключом шифра, называемого
``поворотная решетка'',
является трафарет, изготовленный из квадратного листа
клетчатой бумаги размера  ( ( - четно). Некоторые из
клеток вырезаются. Одна из сторон трафарета помечена. При наложении
этого трафарета на чистый лист бумаги четырьмя возможными способами
(помеченной стороной вверх, вправо, вниз, влево) его вырезы полностью
покрывают всю площадь квадрата, причем каждая клетка оказывается под
вырезом ровно один раз. - четно). Некоторые из
клеток вырезаются. Одна из сторон трафарета помечена. При наложении
этого трафарета на чистый лист бумаги четырьмя возможными способами
(помеченной стороной вверх, вправо, вниз, влево) его вырезы полностью
покрывают всю площадь квадрата, причем каждая клетка оказывается под
вырезом ровно один раз.
Буквы сообщения, имеющего длину  , последовательно
вписываются в вырезы трафарета, сначала наложенного на чистый лист
бумаги помеченной стороной вверх. После заполнения всех вырезов
трафарета буквами сообщения трафарет располагается в следующем
положении и т.д. После снятия трафарета на листе бумаги оказывается
зашифрованное сообщение. , последовательно
вписываются в вырезы трафарета, сначала наложенного на чистый лист
бумаги помеченной стороной вверх. После заполнения всех вырезов
трафарета буквами сообщения трафарет располагается в следующем
положении и т.д. После снятия трафарета на листе бумаги оказывается
зашифрованное сообщение.
Найдите число различных ключей для произвольного четного
числа  . .
1.2. В адрес олимпиады пришло зашифрованное сообщение:
Найдите исходное сообщение, если известно, что
шифрпреобразование
заключалось в следующем.
Пусть
 , ,  - корни трехчлена - корни трехчлена  .
К порядковому номеру каждой буквы в
стандартном русском алфавите (33 буквы) прибавлялось значение
многочлена .
К порядковому номеру каждой буквы в
стандартном русском алфавите (33 буквы) прибавлялось значение
многочлена
 , вычисленное
либо при , вычисленное
либо при  , либо при , либо при  (в неизвестном нам
порядке), а затем полученное число заменялось соответствующей ему
буквой. (в неизвестном нам
порядке), а затем полученное число заменялось соответствующей ему
буквой.
1.3. Для передачи информации от резидента Гарриваса в
Нагонии только что внедренному разведчику был установлен следующий
порядок.
Все сообщения резидента определены заранее и пронумерованы
числами
 . Разведчик, обладающий
феноменальной памятью, полностью запомнил соответствие между
сообщениями и их номерами. Теперь для того, чтобы передать
информацию разведчику, достаточно было сообщить ему лишь
соответствующее число. . Разведчик, обладающий
феноменальной памятью, полностью запомнил соответствие между
сообщениями и их номерами. Теперь для того, чтобы передать
информацию разведчику, достаточно было сообщить ему лишь
соответствующее число.
Для передачи числа в условленном месте оставлялась равная
этому числу денежная сумма.
На момент разработки операции в Нагонии имели хождение
денежные купюры достоинством 1,3,7 и 10 бут (бут - денежная
единица Нагонии). Однако в результате денежной реформы купюры
достоинством 1 и 3 бут были изъяты из обращения.
Выясните, начиная с какого номера можно передать разведчику
любое сообщение, пользуясь только оставшимися в обращении купюрами.
1.4. Сколько существует упорядоченных пар натуральных чисел  и
и  , для которых известны их наибольший общий делитель , для которых известны их наибольший общий делитель  и
их наименьшее общее кратное и
их наименьшее общее кратное  . Сформулируйте ответ и в общем
случае, используя канонические разложения . Сформулируйте ответ и в общем
случае, используя канонические разложения 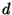 и и  на простые
множители. на простые
множители.
1.5. Дана криптограмма:

Восстановите цифровые значения букв, при которых справедливы
все указанные равенства, если разным буквам соответствуют различные
цифры. Расставьте буквы в порядке возрастания их цифровых значений и
получите искомый текст.
1.6. Одна фирма предложила устройство для автоматической
проверки пароля. Паролем может быть любой непустой
упорядоченный набор букв в алфавите  . Будем обозначать
такие наборы большими латинскими буквами. Устройство
перерабатывает введенный в него набор . Будем обозначать
такие наборы большими латинскими буквами. Устройство
перерабатывает введенный в него набор 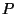 в набор в набор  .
Отображение .
Отображение  держится в секрете, однако про него известно,
что оно определено не для каждого набора букв и обладает следующими
свойствами. Для любого набора букв держится в секрете, однако про него известно,
что оно определено не для каждого набора букв и обладает следующими
свойствами. Для любого набора букв 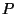
1)  ; ;
2)
 ; ;
3) набор  получается из набора получается из набора  выписыванием букв
в обратном порядке. выписыванием букв
в обратном порядке.
Устройство признает предъявленный пароль верным, если  .
Например, трехбуквенный набор .
Например, трехбуквенный набор  является верным паролем, так как является верным паролем, так как
 . Подберите верный пароль, состоящий
более чем из трех букв. . Подберите верный пароль, состоящий
более чем из трех букв.
Next: Задачи второй олимпиады
Up: 7.5. Условия задач олимпиад
Previous: 7.5. Условия задач олимпиад
Contents: Содержание
| 
