Next: Задачи четвертой олимпиады
Up: 7.5. Условия задач олимпиад
Previous: Задачи второй олимпиады
Contents: Содержание
3.1. Установите, можно ли создать проводную телефонную сеть
связи, состоящую из 993 абонентов, каждый из которых был бы связан
ровно с 99 другими.
3.2. Шифрпреобразование простой замены в алфавите
 , состоящем из , состоящем из  различных букв,
заключается в замене каждой буквы шифруемого текста буквой того же
алфавита, причем разные буквы заменяются разными. Ключом шифра простой
замены называется таблица, в которой указано, какой буквой надо
заменить каждую букву алфавита различных букв,
заключается в замене каждой буквы шифруемого текста буквой того же
алфавита, причем разные буквы заменяются разными. Ключом шифра простой
замены называется таблица, в которой указано, какой буквой надо
заменить каждую букву алфавита  . Если слово СРОЧНО
зашифровать простой заменой с помощью ключа: . Если слово СРОЧНО
зашифровать простой заменой с помощью ключа:
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Э |
Ю |
Я |
|
Ч |
Я |
Ю |
Э |
Ы |
Ь |
Щ |
Ш |
Ц |
Х |
Ф |
У |
Б |
Д |
Т |
З |
В |
Р |
П |
М |
Л |
К |
А |
И |
О |
Ж |
Е |
С |
Г |
Н |
|
то получится слово ВЗДАБД. Зашифровав полученное слово с
помощью того же ключа еще раз, получим слово ЮШЫЧЯЫ.
Сколько всего различных слов можно получить, если указанный процесс
шифрования продолжать неограниченно?
3.3. Сообщение, зашифрованное в пункте А шифром простой
замены в алфавите из букв русского языка и знака пробела (-)
между словами, передается в пункт Б отрезками по 12 символов. При
передаче очередного отрезка сначала передаются символы, стоящие на
четных местах в порядке возрастания их номеров, начиная со второго, а
затем - символы, стоящие на нечетных местах (также в порядке
возрастания их номеров), начиная с первого. В пункте B полученное
шифрованное сообщение дополнительно шифруется с помощью некоторого
другого шифра простой замены в том же алфавите, а затем таким же
образом, как и из пункта А, передается в пункт В. По перехваченным в
пункте В отрезкам:
|
С |
О |
- |
Г |
Ж |
Т |
П |
Н |
Б |
Л |
Ж |
О |
|
Р |
С |
Т |
К |
Д |
К |
С |
П |
Х |
Е |
У |
Б |
|
- |
Е |
- |
П |
Ф |
П |
У |
Б |
- |
Ю |
О |
Б |
|
С |
П |
- |
Е |
О |
К |
Ж |
У |
У |
Л |
Ж |
Л |
|
С |
М |
Ц |
Х |
Б |
Э |
К |
Г |
О |
Щ |
П |
Ы |
|
У |
Л |
К |
Л |
- |
И |
К |
Н |
Т |
Л |
Ж |
Г
|
|
восстановите исходное сообщение, зная, что в одном из переданных отрезков
зашифровано слово КРИПТОГРАФИЯ.
3.4. Дана последовательность чисел
 в
которой в
которой  есть последняя цифра числа есть последняя цифра числа  . Докажите, что эта
последовательность периодическая и ее наименьший период равен 20. . Докажите, что эта
последовательность периодическая и ее наименьший период равен 20.
3.5. Исходное сообщение, состоящее из букв русского алфавита и
знака пробела
(-) между словами, преобразуется в цифровое сообщение
заменой каждого его символа парой цифр согласно следующей таблице:
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Э |
Ю |
Я |
- |
|
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Для зашифрования полученного цифрового сообщения используется отрезок
последовательности из задачи 3.4, начинающийся с
некоторого члена  . При зашифровании каждая цифра сообщения
складывается с соответствующей цифрой отрезка и заменяется последней
цифрой полученной суммы. Восстановите сообщение: . При зашифровании каждая цифра сообщения
складывается с соответствующей цифрой отрезка и заменяется последней
цифрой полученной суммы. Восстановите сообщение:
|
2339867216458160670617315588 |
3.6. Равносторонний треугольник  разбит на четыре части
так, как показано на рисунке, где разбит на четыре части
так, как показано на рисунке, где 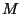 и и 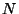 - середины сторон - середины сторон  и
и  соответственно. Известно, что соответственно. Известно, что  и и
 . В каком
отношении точки . В каком
отношении точки  и и  делят сторону делят сторону 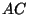 , если известно, что из
этих частей можно составить квадрат? , если известно, что из
этих частей можно составить квадрат?
Next: Задачи четвертой олимпиады
Up: 7.5. Условия задач олимпиад
Previous: Задачи второй олимпиады
Contents: Содержание
|

