




Вперед: 12.2.4 Другие методы
Вверх: 12.2 Факторизация чисел с экспоненциальной сложностью
Назад: 12.2.2 Метод Полларда
Содержание
Предметный указатель
12.2.3 Метод Полларда -- Штрассена
Самым популярным среди алгоритмов факторизации целых чисел
с экспоненциальной сложностью является метод Полларда --
Штрассена, имеющий детерминированную оценку сложности
 . Подробное описание метода
можно найти в [Poll74], [Pom82], [Sch1],
[Stra]. Он основан на следующей теореме: . Подробное описание метода
можно найти в [Poll74], [Pom82], [Sch1],
[Stra]. Он основан на следующей теореме:
Теорема 3.
Пусть  -- натуральное число, -- натуральное число,  .
Тогда для любого натурального .
Тогда для любого натурального 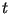 наименьший простой
делитель числа наименьший простой
делитель числа  может быть найден за может быть найден за
 арифметических операций. арифметических операций.
Для нахождения наименьшего простого делителя числа  по
методу Полларда -- Штрассена нужно положить по
методу Полларда -- Штрассена нужно положить
![$ z=\left[n^{1/4}\right]+1$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1508.gif) , ,  , ,  и найти
наименьший простой делитель и найти
наименьший простой делитель  за за
 арифметических операций согласно теореме 3.
Найденный делитель будет наименьшим простым делителем
арифметических операций согласно теореме 3.
Найденный делитель будет наименьшим простым делителем  ввиду следующих соображений. Если
ввиду следующих соображений. Если  -- наименьший
простой делитель -- наименьший
простой делитель  , то , то
 и,
следовательно, и,
следовательно,  делит делит  . Поэтому . Поэтому  является также
наименьшим простым делителем является также
наименьшим простым делителем
 . .





Вперед: 12.2.4 Другие методы
Вверх: 12.2 Факторизация чисел с экспоненциальной сложностью
Назад: 12.2.2 Метод Полларда
Содержание
Предметный указатель
|

