




Вперед: 12.3.2 Методы ускорения алгоритма Диксона
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Содержание
Предметный указатель
12.3.1 Алгоритм Диксона
В алгоритме Диксона мы будем обозначать через 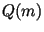 наименьший неотрицательный вычет
наименьший неотрицательный вычет
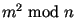 , а через , а через  -- некоторую константу такую, что
-- некоторую константу такую, что 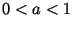 . Множество
простых чисел, не превосходящих . Множество
простых чисел, не превосходящих 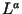 , мы будем называть
факторной базой и обозначать через , мы будем называть
факторной базой и обозначать через
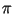 . Алгоритм Диксона заключается в следующем:
1.
Выбрать случайное . Алгоритм Диксона заключается в следующем:
1.
Выбрать случайное
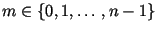 и
вычислить и
вычислить 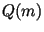 . .
2.
Пробными делениями попытаться полностью разложить
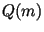 в произведение простых в произведение простых 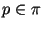 . .
3.
В случае успеха, т. е. если
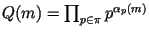 , где , где
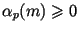 , запомнить , запомнить  , , 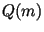 и вектор и вектор
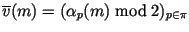 ,
показателей, приведенных по модулю 2. Делать перебор ,
показателей, приведенных по модулю 2. Делать перебор  до тех пор, пока не будет найдено
до тех пор, пока не будет найдено 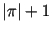 чисел, для
которых чисел, для
которых 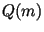 полностью разлагаются в факторной базе. полностью разлагаются в факторной базе.
4.
Найти (например, с помощью гауссова исключения)
некоторое соотношение линейной зависимости
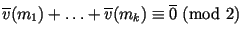 между
вычисленными на предыдущем этапе векторами между
вычисленными на предыдущем этапе векторами
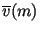 : :
5.
Найденное на предыдущем этапе соотношение означает,
что
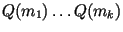 является квадратом натурального
числа, которое мы обозначим через является квадратом натурального
числа, которое мы обозначим через  . С другой стороны, . С другой стороны,
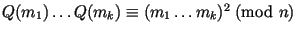 .
Поэтому для .
Поэтому для
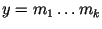 имеем имеем
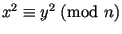 .
Теперь если .
Теперь если
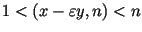 для некоторого для некоторого
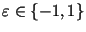 , то , то
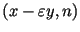 --
искомый нетривиальный делитель --
искомый нетривиальный делитель  . .
В работе [Dix] доказано, что если
 составное, то для случайно построенной пары составное, то для случайно построенной пары 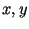 ,
удовлетворяющей условию ,
удовлетворяющей условию
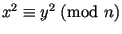 , вероятность
того, что , вероятность
того, что
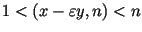 для некоторого для некоторого
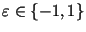 , не меньше 1/2. , не меньше 1/2.
В работе [Pom82] показано, что если в алгоритме
Диксона перебрано
![$ \left[L^b\right]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1545.gif) случайных значений случайных значений  и на этапе 4 использовано гауссово исключение, то сложность
этого алгоритма составляет
и на этапе 4 использовано гауссово исключение, то сложность
этого алгоритма составляет
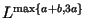 арифметических операций. Согласно этой же работе, для
нахождения нужного количества чисел
арифметических операций. Согласно этой же работе, для
нахождения нужного количества чисел  таких, что Q(m)
полностью разлагаются в факторной базе, достаточно
перебрать таких, что Q(m)
полностью разлагаются в факторной базе, достаточно
перебрать
![$ \left[L^b\right]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1545.gif) случайных значений случайных значений  , где , где
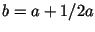 . В частности, при . В частности, при 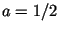 и и
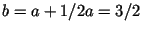 сложность алгоритма Диксона составляет
сложность алгоритма Диксона составляет 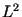 арифметических
операций. арифметических
операций.





Вперед: 12.3.2 Методы ускорения алгоритма Диксона
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Содержание
Предметный указатель
|

