




Вперед: 12.3.3 Алгоритм Бриллхарта - Моррисона
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3.1 Алгоритм Диксона
Содержание
Предметный указатель
12.3.2 Методы ускорения алгоритма Диксона
На практике в алгоритме Диксона часто используют
один или несколько описываемых ниже методов
ускорения его работы.
1. Стратегия LP (использование больших
простых). Впервые она предложена в работе
[BrMor] и обычно используется на практике.
Пусть мы раскладываем 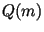 на множители. Предположим, что
после деления на все на множители. Предположим, что
после деления на все 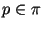 осталась некоторая не
разложившаяся на множители часть осталась некоторая не
разложившаяся на множители часть  . Ясно, что . Ясно, что  .
Если окажется, что при этом .
Если окажется, что при этом
 , то , то  --
простое число. Тогда мы включаем --
простое число. Тогда мы включаем  в факторную базу в факторную базу
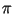 и храним также найденное значение и храним также найденное значение 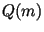 . Это
увеличивает длину векторов . Это
увеличивает длину векторов  . .
В работе [Pom82] показано, что теоретическая оценка
сложности алгоритма Диксона с использованием стратегии LP
не улучшается.
2. Стратегия PS (метод Полларда --
Штрассена). В алгоритме Диксона можно использовать
метод Полларда -- Штрассена, описанный в п. 12.2.3,
для разложения 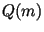 на множители. А именно, мы полагаем на множители. А именно, мы полагаем
![$ y=\left(\left[L^{a/2}\right]+1\right)$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1554.gif) , ,  и находим
наименьший простой делитель и находим
наименьший простой делитель  согласно
теореме 3. Если согласно
теореме 3. Если  --
наименьший простой делитель --
наименьший простой делитель 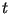 , принадлежащий , принадлежащий 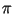 , то , то
 и, следовательно, и, следовательно,  делит делит  .
Поэтому .
Поэтому  является также наименьшим простым делителем является также наименьшим простым делителем
 . Таким образом, мы можем находить наименьшие
простые делители, принадлежащие . Таким образом, мы можем находить наименьшие
простые делители, принадлежащие 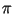 . .
Можно показать, что при использовании стратегии PS в оценке
сложности алгоритма Диксона (см. п. 12.3.1) вместо
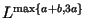 появится появится
 . В
частности, при . В
частности, при
 , , 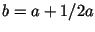 получаем, что
алгоритм Диксона со стратегией PS работает за получаем, что
алгоритм Диксона со стратегией PS работает за
 арифметических операций.
арифметических операций.
3. Стратегия EAS (ранний обрыв). Пусть
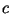 и и  -- некоторые константы такие, что -- некоторые константы такие, что
 . В обычном алгоритме Диксона мы разлагали . В обычном алгоритме Диксона мы разлагали
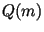 на на 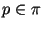 . В алгоритме Диксона со стратегией EAS
мы сначала разлагаем . В алгоритме Диксона со стратегией EAS
мы сначала разлагаем 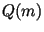 на простые множители, не
превосходящие на простые множители, не
превосходящие
 , и, если неразложившаяся часть , и, если неразложившаяся часть
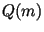 больше, чем больше, чем  , то отбрасываем это значение , то отбрасываем это значение
 и переходим к следующему. В работе [Pom82]
приведен анализ этой стратегии. В частности, показано, что
алгоритм Диксона со стратегией EAS при и переходим к следующему. В работе [Pom82]
приведен анализ этой стратегии. В частности, показано, что
алгоритм Диксона со стратегией EAS при
 , ,
 , ,
 делает делает
 арифметических операций. При этом
арифметических операций. При этом
 . .
Можно также применять стратегию EAS с несколькими обрывами.
4. Методы поиска соотношений линейной
зависимости. На
этапе 4 алгоритма Диксона для нахождения соотношения
линейной зависимости нужно решать разреженную систему
линейных уравнений над полем
 . Метод гауссова
исключения не является оптимальным для этой цели. В работах
[Lanc], [CopW], [Wied], [Bril] описаны
более совершенные способы решения разреженных систем
линейных уравнений над полем . Метод гауссова
исключения не является оптимальным для этой цели. В работах
[Lanc], [CopW], [Wied], [Bril] описаны
более совершенные способы решения разреженных систем
линейных уравнений над полем
 . В частности, алгоритм
Копперсмита -- Винограда решает систему линейных уравнений
от . В частности, алгоритм
Копперсмита -- Винограда решает систему линейных уравнений
от  неизвестных за неизвестных за
 арифметических операций.
арифметических операций.





Вперед: 12.3.3 Алгоритм Бриллхарта - Моррисона
Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью
Назад: 12.3.1 Алгоритм Диксона
Содержание
Предметный указатель
|

