Разделы

• 6.2.1 Долгопериодические приливы
• 6.2.2 Суточные приливы
• 6.2.3 Полусуточные приливы

6.2 Типы приливных волн

Все наблюдаемые приливные явления делятся на полусуточные, суточные и долгопериодические. Вернемся к формуле (6.13), в которой переменной величиной будем считать только зенитное расстояние. Известно, что

где 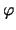-- широта места наблюдения, -- склонение светила. -- часовой угол, поэтому

Подставляя полученное выражение в (6.13), будем иметь

Первая группа членов не зависит от часового угла. Здесь переменная величина только склонение, которое меняется медленно. Это долгопериодная часть приливообразующего потенциала. Второй член приведенной суммы имеет аргументом -- часовой угол, который меняется от 0 до 2 за одни сутки. Следовательно, он формирует суточный прилив. Третий член с аргументом 2, как нетрудно догадаться -- полусуточный.

6.2.1 Долгопериодические приливы

Будем помечать долгопериодическую компоненту приливного потенциала штрихом. Тогда

Окончательно

(6.14)

Этот прилив имеет период, равный половину периода обращения притягивающего светила за счет изменение склонения. Если это -- лунный прилив, то период его две недели, если солнечный -- полгода. Линия узлов (приливообразующий потенциал равен нулю) проходит по параллелям, для которых , то есть .

Долгопериодический прилив имеет зональную конфигурацию, он изменяет момент инерции Земли относительно оси вращения и, следовательно, изменяет и ее скорость вращения. Этот прилив можно наблюдать с помощью радиотелескопов со сверхдлинной базой, позволяющих обнаруживать ничтожно малые изменения в продолжительности суток.

6.2.2 Суточные приливы

Они определяются вторым членом в приливообразующем потенциале

(6.15)

За одни сутки часовой угол изменяется на , что и определяет периодичность этого члена потенциала. Небольшие отличия от суток вносит изменение склонения светила. У этого прилива линии узлов проходят по меридиану ( часов) и по экватору. Поверхность шара оказывается поделенной на четыре части, причем южное полушарие повторяет северное, но с другим знаком. Такую конфигурацию прилива мы относим к тессеральным. Этот прилив не изменяет момента инерции, и, следовательно, не меняет угловую скорость вращения Земли.

6.2.3 Полусуточные приливы

Третий тип приливов определяется членом

(6.16)

Изменение аргумента на достигается за 12 часов, что и сообщает этой части приливообразующего потенциала полусуточную периодичность. Линии узлов -- два меридиана с часовыми углами   часа и  часов. Поверхность Земли оказывается снова рассеченной на четыре части, на четыре сектора. Отсюда и секториальная конфигурация полусуточного прилива.

Подъем уровенной поверхности будет наблюдаться в секторе, обращенном в сторону притягивающего тела. В противоположном секторе -- также подъем. В секторах, ориентированных под углом -- минимум.

Периоды приливообразующего потенциала, подсчитанные только по часовому углу, слишком упрощенный подход. Во первых, мы рассматривали только одно притягивающее тело -- Луну, хотя значительный вклад и земные приливы вносит и Солнце. Приливы от Луны и Солнца, строго говоря, нельзя рассматривать как сумму приливов отдельно от Луны и от Солнца, так как сами формулы для вычисления потенциала нелинейные. Линейным образом этот потенциал зависит лишь от масс этих небесных тел, что же касается геометрии -- то нелинейная зависимость очевидная. Приливную силу, действующую на планету, можно представить в виде суммы гармоник с аргументами, выражающиеся линейной комбинацией углов, которые можно представить в виде , где

	-- среднее лунное время,
	-- средняя долгота Луны,
	-- средняя долгота Солнца,
	-- долгота перигея Луны,
	-- долгота перигея Солнца.

Аргументным числом называется шестизначное число .

Приведем здесь перечень основных приливных волн (по П.Мельхиору "Земные приливы"):

волна	период	аргументное число	периодическая функция
	12.25	(255.555)
	12.39	(245.655)
	25.49	(145.555)
	23.56	(165.555)
	две недели	(075.555)
	тропический месяц	(065.455)
	12.00	(273.555)
	24.04	(163.555)

В приведенной таблице период указан в часах и минутах. Полусуточные приливы -- это , и . Первые два связаны с Луной, третий -- с Солнцем. Суточные приливы это (Луна), и (Солнце). Поскольку периоды приливных волн известны точно, так как движения небесных тел подчинятся законам небесной механики, то для исследования приливных волн применяют методы гармонического анализа. Представление приливных явлений гармониками введено еще известным геофизиком Дарвиным (1883). Изложенная выше классификация гармоник предложена Дудсоном. Им же, а затем и Леколазе предложены методы гармонического анализа. Среди российских ученых известен метод Перцева, который позволяет не только выделять отдельные гармоники, но и исключать дрейф в записи приливных волн.