|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.3. Взаимодействия элементов
симметрии
I.3.1. Теорема Эйлера
Результат сочетания двух вращений
вокруг пересекающихся поворотных осей легко
увидеть, рассмотрев движение точки на
поверхности сферы (рис. 5). Пусть А и
В - точки выхода двух пересекающихся в центре О
сферы поворотных осей с элементарными углами
поворота  и и  соответственно.
Направления вращений указаны стрелками. Для
доказательства на поверхности сферы проведем
дуги больших кругов (экваторы) а - а и в -
в, полюсами которых служат выходы исходных
осей А и В соответственно. Рассмотрим
последовательные вращения вокруг указанных осей
некоторой точки 1, выбрав ее на поверхности сферы
так, чтобы после поворота вокруг оси А на угол a
(движение по экватору а - а) она оказалась
на экваторе в - в в положении 2. После
поворота точки 2 на угол b вокруг оси В (движение
по экватору в - в) она попадет в положение
3. Дуга большого круга, проведенная через точки 1 и
3, является экватором с - с по отношению к
полюсу в точке С. При этом движение точки 1 по
экватору с - с в точку 3 можно считать
поворотом на угол g вокруг оси, выходящей в полюсе
С. Таким образом, два поворота против часовой
стрелки вокруг пересекающихся осей А и В можно
заменить поворотом в том же направлении вокруг
третьей оси С: А соответственно.
Направления вращений указаны стрелками. Для
доказательства на поверхности сферы проведем
дуги больших кругов (экваторы) а - а и в -
в, полюсами которых служат выходы исходных
осей А и В соответственно. Рассмотрим
последовательные вращения вокруг указанных осей
некоторой точки 1, выбрав ее на поверхности сферы
так, чтобы после поворота вокруг оси А на угол a
(движение по экватору а - а) она оказалась
на экваторе в - в в положении 2. После
поворота точки 2 на угол b вокруг оси В (движение
по экватору в - в) она попадет в положение
3. Дуга большого круга, проведенная через точки 1 и
3, является экватором с - с по отношению к
полюсу в точке С. При этом движение точки 1 по
экватору с - с в точку 3 можно считать
поворотом на угол g вокруг оси, выходящей в полюсе
С. Таким образом, два поворота против часовой
стрелки вокруг пересекающихся осей А и В можно
заменить поворотом в том же направлении вокруг
третьей оси С: А . В . В = С = С . В этом суть
известной "осевой" теоремы Эйлера, лежащей
в основе теории симметрии кристаллов. Нетрудно
понять, что комбинация вращений вокруг трех
пересекающихся осей соответствует операции
идентичности, оставляющей точку на месте: А . В этом суть
известной "осевой" теоремы Эйлера, лежащей
в основе теории симметрии кристаллов. Нетрудно
понять, что комбинация вращений вокруг трех
пересекающихся осей соответствует операции
идентичности, оставляющей точку на месте: А . В . В . С- . С- = 1. = 1.
Для получения конкретных значений
угловых величин следует прибегнуть к построению
Эйлера (см. [58]), использующему половинные
элементарные углы поворотов осей, что особенно
удобно при рассмотрении взаимодействия осей 2-го
порядка ( = 180o). = 180o).
При доказательстве теоремы все
построения, как и в рассмотренном выше случае,
проводятся на поверхности сферы (рис.6).
Точки А и В - выходы пересекающихся в центре
сферы О двух поворотных осей: ОА (с элементарным
углом поворота  ) и ОВ (с углом ) и ОВ (с углом  ). Угол между этими осями соответствует
отрезку АВ дуги большого круга, проходящей через
их выходы. ). Угол между этими осями соответствует
отрезку АВ дуги большого круга, проходящей через
их выходы.
Проведем на сфере дуги АМ и АМ', BN и BN',
образующие с дугой АВ углы  /2 и /2 и  /2 соответственно: /2 соответственно: 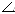 МАВ = МАВ = 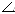 М'АВ = М'АВ = /2, /2, 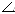 NBA = NBA = 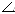 N'BA = N'BA =  /2. /2.
Обозначим точки пересечения дуг АМ с ВN
и АМ' с ВN' буквами С и С' соответственно.
Рассмотрим движение точки С на сфере. В
результате поворота вокруг оси А на
угол a против часовой стрелки точка С перейдет в
положение С'. Последующий поворот точки С' вокруг
оси В на
угол a против часовой стрелки точка С перейдет в
положение С'. Последующий поворот точки С' вокруг
оси В на угол на угол  в том же
направлении вернет ее в исходное положение С.
Таким образом, комбинация вращений вокруг осей А в том же
направлении вернет ее в исходное положение С.
Таким образом, комбинация вращений вокруг осей А и В и В оставит точку С
на месте. Это значит, что третье - результирующее
- вращение может происходить исключительно
вокруг оси, выход которой совпадает с точкой С,
ибо только в этом случае будет выполняться
условие А оставит точку С
на месте. Это значит, что третье - результирующее
- вращение может происходить исключительно
вокруг оси, выход которой совпадает с точкой С,
ибо только в этом случае будет выполняться
условие А . В . В . С- . С- = 1, и точка
С при повороте вокруг третьей оси останется на
месте. Величину угла = 1, и точка
С при повороте вокруг третьей оси останется на
месте. Величину угла  легко измерить,
рассмотрев полное перемещение точки А: поворот
вокруг оси А легко измерить,
рассмотрев полное перемещение точки А: поворот
вокруг оси А оставит точку на
месте, поворот вокруг оси В оставит точку на
месте, поворот вокруг оси В переведет
точку А в положение А'. В результате образуются
два равных треугольника: переведет
точку А в положение А'. В результате образуются
два равных треугольника: 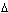 АВС = АВС = 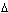 А'ВС, ибо А'ВС, ибо 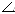 АВС = АВС = 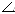 А'ВС = А'ВС = 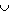 /2 и /2 и 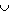 АВ = АВ = 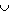 А'В по построению. Следовательно, А'В по построению. Следовательно, 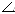 АСВ = АСВ = 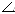 А'СВ. Обозначив
каждый из них А'СВ. Обозначив
каждый из них  /2, получим
элементарный угол поворота /2, получим
элементарный угол поворота  для оси С для оси С , выходящей в точке С. , выходящей в точке С.
В результате проведенных построений
получен сферический треугольник АВС, углы А, В и С
при вершинах которого равны половинам
элементарных углов поворота осей, выходящих в
его вершинах, т.е. А = =  /2, В = /2, В =  /2 и С = /2 и С =  /2. Стороны такого
сферического треугольника а = = /2. Стороны такого
сферического треугольника а = = 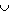 ВС, в
= ВС, в
= 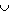 АС, с = АС, с = 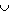 АВ
соответствуют углам между этими осями. АВ
соответствуют углам между этими осями.
Расчеты порядков осей и углов между
ними можно производить по формулам сферической
тригонометрии [24] - раздела математики,
рассматривающего только фигуры, образованные
дугами больших кругов, - сферические
треугольники, каждый из которых может быть
охарактеризован шестью элементами: тремя
сторонами - дугами (а, в, с) - и углами между
ними (А, В, С). Основные формулы сферической
тригонометрии связывают четыре или пять
элементов сферического треугольника, т.е. дают
возможность по трем или четырем данным его
элементам определить остальные.
|

