|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава III. Координатные системы,
категории, сингонии
32 кристаллографические группы
симметрии разбиваются на семейства - категории, каждая из которых
характеризуется определенными соотношениями
между координатными осями -
степенью их эквивалентности. Координатные оси в
кристаллах выбираются, как правило, по
особым направлениям, т.е. осям симметрии (n), нормалям к плоскостям симметрии (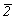 ), а при их отсутствии - по возможным или действительным
ребрам кристаллических многогранников,
совпадающим с трансляционными векторами
пространственной решетки ), а при их отсутствии - по возможным или действительным
ребрам кристаллических многогранников,
совпадающим с трансляционными векторами
пространственной решетки 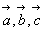 (с. 88). Три возможности
соотношений этих параметров
- a (с. 88). Три возможности
соотношений этих параметров
- a  b b  c, a = b c, a = b  c и a = b = c - позволяют
распределить кристаллографические координатные
системы по трем категориям: низшей, средней и высшей
соответственно. c и a = b = c - позволяют
распределить кристаллографические координатные
системы по трем категориям: низшей, средней и высшей
соответственно.
Полная неэквивалентность
координатных направлений (a
 b b  c) предполагает
отсутствие осей симметрии высшего порядка. Таким
образом, к низшей категории относятся
следующие группы симметрии: c) предполагает
отсутствие осей симметрии высшего порядка. Таким
образом, к низшей категории относятся
следующие группы симметрии:
без особых направлений - 1 и 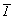 , ,
с одним особым направлением -
2, m (=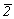 ), ), 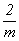 , ,
с тремя особыми направлениями - 222, mm2, mmm.
В первом случае отсутствие особых
направлений приводит к косоугольной системе
самого общего вида: a  b ? b ?  , ,      ( где ( где  , ,  , ,  - углы между
координатными осями YZ, XZ и XY соответственно). - углы между
координатными осями YZ, XZ и XY соответственно).
Группы симметрии с единой
координатной системой объединяются в одно
семейство, называемое сингонией 1 (греч. 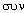 (син) - вместе; (син) - вместе; 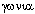 (гониа) - угол). В данном случае косоугольная
координатная система определила и ее название: триклинная (греч. (гониа) - угол). В данном случае косоугольная
координатная система определила и ее название: триклинная (греч. 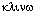 (клинос) - косой
угол). (клинос) - косой
угол).
Группа симметрии, содержащая лишь одно
особое направление, характеризуется
координатной системой с одним непрямым углом
(углом между координатными осями, выбранными
параллельно ребрам кристалла в плоскости,
перпендикулярной единственному особому
направлению). Отсюда название сингонии с такой
координатной системой (a  b b  c, c,  = =  = 90o , = 90o ,   90o 90o  120o ) - моноклинная 2. 120o ) - моноклинная 2.
При наличии в группе симметрии трех
особых направлений - а
ими в низшей категории могут быть лишь
поворотные или (и) инверсионные оси 2-го порядка - углы между координатными осями
оказываются прямыми. В противном случае
возникнут оси высшего порядка, характерные для
иных категорий. Такая прямоугольная
координатная система с параметрами a  b b  c, c,  = =  = =  = 90o
обслуживает
группы ромбической 3 сингонии. = 90o
обслуживает
группы ромбической 3 сингонии.
Условие эквивалентности двух
координатных направлений (a
= b  c) в средней категории
может быть выполнено лишь при
наличии в группе симметрии единственной оси
высшего порядка - главной оси
группы, которую принято совмещать с вертикальной
координатной осью Z. Две другие координатные оси - X и Y
- выбирают
по осям 2-го порядка, поворотным или инверсионным,
а при их отсутствии - параллельно
действительным или возможным ребрам кристаллов
в плоскости, перпендикулярной главной оси. Таким
образом, два угла координатной системы ( c) в средней категории
может быть выполнено лишь при
наличии в группе симметрии единственной оси
высшего порядка - главной оси
группы, которую принято совмещать с вертикальной
координатной осью Z. Две другие координатные оси - X и Y
- выбирают
по осям 2-го порядка, поворотным или инверсионным,
а при их отсутствии - параллельно
действительным или возможным ребрам кристаллов
в плоскости, перпендикулярной главной оси. Таким
образом, два угла координатной системы ( и и
 )
оказываются прямыми, третий же угол ( )
оказываются прямыми, третий же угол ( ) между
горизонтальными осями X и Y соответствует
элементарному углу поворота главной оси: для оси
4-го порядка ) между
горизонтальными осями X и Y соответствует
элементарному углу поворота главной оси: для оси
4-го порядка  = 90o , для осей 3-го и 6-го
порядков g = 120o .
Различие углов g приводит к двум
координатным системам, а следовательно, и
к двум сингониям в средней категории: тетрагональной ( a = b = 90o , для осей 3-го и 6-го
порядков g = 120o .
Различие углов g приводит к двум
координатным системам, а следовательно, и
к двум сингониям в средней категории: тетрагональной ( a = b  c, c,  = =  = =  = 90o
) и гексагональной 4 ( a = b = 90o
) и гексагональной 4 ( a = b  c, c,  = = = 90o , = 90o ,  = 120o ). = 120o ).
При таком выделении двух сингоний в
основу заложена единая координатная система;
группы с осями 3-го и 6-го порядков попадают в одну - гексагональную -
сингонию, которую, в свою очередь,
можно подразделить на две подсингонии: тригональную, с
главной осью 3-го (3 или 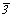 )
и собственно гексагональную, с главной осью 6-го порядка (6 или )
и собственно гексагональную, с главной осью 6-го порядка (6 или 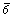 ). Если же в основу выделения
сингоний заложен такой формальный признак, как
порядок главной оси, то в этом случае можно
выделить как две самостоятельные гексагональную и тригональную
сингонии, каждая из которых характеризуется
определенным порядком главной оси (6
или 3 соответственно). ). Если же в основу выделения
сингоний заложен такой формальный признак, как
порядок главной оси, то в этом случае можно
выделить как две самостоятельные гексагональную и тригональную
сингонии, каждая из которых характеризуется
определенным порядком главной оси (6
или 3 соответственно).
В литературе можно встретить описание
кристаллов с единственной осью 3-го порядка в
устаревшей установке Миллера: a =
b = c,  = =  = =   90o . Однако в этом случае
координатные оси оказываются выбранными не по
особым направлениям (как в общепринятой
установке), а по ребрам кристаллов,
равнонаклонным к оси 3. 90o . Однако в этом случае
координатные оси оказываются выбранными не по
особым направлениям (как в общепринятой
установке), а по ребрам кристаллов,
равнонаклонным к оси 3.
Если точечная симметрия групп
характеризуется наличием четырех осей 3-го
порядка, то все три координатные оси, выбранные
по особым направлениям, эквивалентны. При этом
оси 3-го порядка оказываются равнонаклонны к
выбранным координатным направлениям, что возможно лишь
в прямоугольной координатной системе высшей
категории с параметрами a = b = c,  = =  = =  =
90o кубической
сингонии. =
90o кубической
сингонии.
В классической кристаллографии в
пределах каждой сингонии принято следующее
деление групп симметрии в зависимости от их
порядка (см. с. 28): голоэдрические -
группы высшего порядка
данной сингонии (название связано с числом
граней общей простой формы кристаллов,
максимальным для данного класса (от греч. 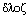 (голо) - полный, весь; (голо) - полный, весь; 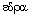 (эдра) - грань, отсюда и название групп высшего
порядка данной сингонии: голоэдрия); остальные группы данной
сингонии являются подгруппами голоэдрической
группы; мероэдрические - группы пониженного порядка
(греч. (эдра) - грань, отсюда и название групп высшего
порядка данной сингонии: голоэдрия); остальные группы данной
сингонии являются подгруппами голоэдрической
группы; мероэдрические - группы пониженного порядка
(греч.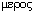 (мерос) - часть), которые подразделяются, в свою очередь, на гемиэдрические
(греч. (мерос) - часть), которые подразделяются, в свою очередь, на гемиэдрические
(греч. 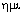 (геми) -
половина) -
группы с порядком вдвое меньшим, чем
голоэдрические группы (гемиэдрия);
тетартоэдрические - порядок
понижен вчетверо ( (геми) -
половина) -
группы с порядком вдвое меньшим, чем
голоэдрические группы (гемиэдрия);
тетартоэдрические - порядок
понижен вчетверо (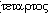 (тетартос) - четвертый, четверть,
тетартоэдрия); огдоэдрические группы с
восьмикратно пониженным порядком (огдоэдрия). (тетартос) - четвертый, четверть,
тетартоэдрия); огдоэдрические группы с
восьмикратно пониженным порядком (огдоэдрия).
Среди гемиэдрических групп выделяют: осевую
гемиэдрию, т.е. подгруппу, содержащую только
оси - элементы симметрии 1-го рода, гемиморфию, гемиморфную
гемиэдрию - группы с единственной полярной
осью, параморфию (параморфную
гемиэдрию) - группы без элементов симметрии 2-й и 3-й позиций
международного символа. Например, в
тетрагональной сингонии группа 16-го порядка 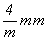 - голоэдрическая. Среди
остальных мероэдрических (4mm, - голоэдрическая. Среди
остальных мероэдрических (4mm, 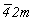 , 422, , 422, 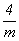 , , 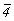 , 4) можно выделить гемиморфную
гемиэдрию - 4mm, осевую гемиэдрию -
422,
параморфную гемиэдрию - , 4) можно выделить гемиморфную
гемиэдрию - 4mm, осевую гемиэдрию -
422,
параморфную гемиэдрию - 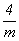 и тетартоэдрические группы - и тетартоэдрические группы - 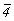 и 4. и 4.
|

