|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава VI. Двухмерные
(плоские) группы симметрии
Под бесконечной двухмерной постройкой
понимают объект двумерного пространства,
обязательными операциями которого служат два
непараллельных вектора переноса - две
трансляции. Группы, характеризующие симметрию
таких построек, играют в кристаллографии большую
роль, являясь двухмерными аналогами
пространственных групп симметрии. Их используют
при описании проекций кристаллических структур,
их сечений, двухмерных сечений распределений
электронной плотности, а также в прикладном
искусстве при описании симметрии рисунков -
разнообразных сетчатых орнаментов.
Вывод двухмерных групп симметрии
удобно осуществить по той же схеме, что и вывод
одномерных групп, исследуя в соответствии с
принципом Кюри сочетания симметрий конечных
фигур и двухмерных решеток - узловых сеток.
Двухмерный бесконечный узор может
быть совмещен с самим собой переносом вдоль
трансляционных пересекающихся векторов 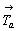 и и  , лежащих в одной плоскости. Периодичность
плоского узора выражается двухмерной
параллелограмматической узловой сеткой - двухмерной
решеткой, его элементом симметрии. Таким
образом, если геометрически одномерную
"решетку" - узловой ряд - достаточно полно и
однозначно характеризуют величина и направление
одного трансляционного вектора , лежащих в одной плоскости. Периодичность
плоского узора выражается двухмерной
параллелограмматической узловой сеткой - двухмерной
решеткой, его элементом симметрии. Таким
образом, если геометрически одномерную
"решетку" - узловой ряд - достаточно полно и
однозначно характеризуют величина и направление
одного трансляционного вектора 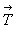 , то минимальным представителем
двухмерной решетки оказывается параллелограмм,
построенный на двух неколлинеарных векторах,
называемый ячейкой
двухмерной решетки. Очевидно, что
подобные ячейки выполняют все двухмерное
пространство без промежутков. , то минимальным представителем
двухмерной решетки оказывается параллелограмм,
построенный на двух неколлинеарных векторах,
называемый ячейкой
двухмерной решетки. Очевидно, что
подобные ячейки выполняют все двухмерное
пространство без промежутков.
Поскольку любой узел можно считать
начальной точкой бесконечного множества
трансляционных векторов, выбор ячейки
неоднозначен. А следовательно, в одной и той же
решетке можно выделить бесконечное множество
ячеек, различающихся как своей формой, так и
величиной (рис. 52). При этом ячейки
могут оказаться либо пустыми (примитивными) с
узлами лишь в вершинах параллелограммов, либо с
дополнительными узлами, не охваченными контуром
ячейки (непримитивными). Все примитивные
ячейки одной и той же решетки равновелики. На
одну такую ячейку приходится один узел решетки.
Отсюда общее число узлов, приходящихся на
непримитивную ячейку, показывает, во сколько раз
она больше примитивной ячейки этой же решетки.
Ячейка, наиболее полно отражающая все
особенности двухмерной решетки, - это
параллелограмм, построенный на двух кратчайших
неколлинеарных трансляционных векторах,
совпадающих с особыми направлениями
максимальной симметрии, а при их отсутствии - с
узловыми рядами. Выбранный таким образом
параллелограмм подчинен кристаллографической
координатной системе, имеет минимальную площадь
и называется элементарной ячейкой. При этом,
если векторы 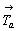 и и  не окажутся минимальными,
то ячейка и соответствующая ей решетка будут непримитивными. не окажутся минимальными,
то ячейка и соответствующая ей решетка будут непримитивными.
Анализ возможных точечных
преобразований симметрии двухмерной решетки в
себя в определенной кристаллографической
координатной системе, т.е. точечных групп
решетки, выявляет различные соотношения
основных минимальных трансляционных векторов 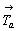 и и  и определенных значений углов между ними.
Возможные сочетания этих величин: и определенных значений углов между ними.
Возможные сочетания этих величин: 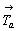 ? ?  , , 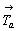 = =  и и   90o , 90o ,  = 90o - приведут к следующим типам
решеток. = 90o - приведут к следующим типам
решеток.
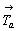   , ,   90o (рис. 53, а). Элементарной ячейкой
такой узловой сетки будет примитивный
параллелограмм. При этом единственным элементом
симметрии указанной решетки (сетки) будет
перпендикулярная к ней ось 2-го порядка, ее группа
симметрии - p112. 90o (рис. 53, а). Элементарной ячейкой
такой узловой сетки будет примитивный
параллелограмм. При этом единственным элементом
симметрии указанной решетки (сетки) будет
перпендикулярная к ней ось 2-го порядка, ее группа
симметрии - p112.
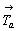   , ,  = 90o (рис. 53,
б). Элементарная ячейка в данном случае будет
иметь форму прямоугольного примитивного
параллелограмма. Группа симметрии такой решетки
- pmm2. = 90o (рис. 53,
б). Элементарная ячейка в данном случае будет
иметь форму прямоугольного примитивного
параллелограмма. Группа симметрии такой решетки
- pmm2.
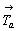 = =  , ,   90o . Равенство
двух неколлинеарных векторов с углом между ними,
отличающимся от 90o , указывает на возможность
присутствия оси симметрии, перпендикулярной
двухмерной решетке (узловой сетке); порядок оси
определяется минимальным углом 90o . Равенство
двух неколлинеарных векторов с углом между ними,
отличающимся от 90o , указывает на возможность
присутствия оси симметрии, перпендикулярной
двухмерной решетке (узловой сетке); порядок оси
определяется минимальным углом  между исходными векторами. между исходными векторами.
Н.В.Беловым предложено выгодно
отличающееся от других доказательство,
касающееся возможных порядков осей, перпендикулярных
узловой сетке [18]. Сначала устанавливается
минимально возможная величина угла между
эквивалентными узловыми рядами, а следовательно,
и максимальный порядок оси симметрии,
перпендикулярной узловой сетке (рис.
54). Предположив, что узел А является точкой
пересечения двух узловых рядов,
характеризующихся одним и тем же минимальным для
данной решетки межузловым расстоянием a,
увидим, что в треугольнике АА1А2
сторона А1А2 должна быть либо равна a,
либо больше a, а следовательно,  > 60o . Таким
образом, если узел А взят на оси Ln,
перпендикулярной к узловой сетке, то ее порядок
не может быть больше шести. > 60o . Таким
образом, если узел А взят на оси Ln,
перпендикулярной к узловой сетке, то ее порядок
не может быть больше шести.
Для решения вопроса о возможных
порядках осей ниже шести надо вспомнить то, что любая
параллелограмматическая сетка всегда обладает
осью симметрии 2-го порядка, перпендикулярной
слою. И если перпендикулярно двухмерной сетке
предположить ось нечетного порядка, то в
результате их взаимодействия возникнет ось с
удвоенным порядком: L2n+1 . L2 = L2(2n+1),
т.е. оси L1 и L3 повысятся до L2
и L6 соответственно, что вполне
допустимо в параллелограмматической сетке,
тогда как ось 5-го порядка в сочетании с
параллельной ей осью L2 даст ось 10-го
порядка, а это противоречит доказанному выше.
Таким образом, угол g между
эквивалентными трансляционными векторами может
быть равен 60, 90 или 120o , т.е. в
параллелограмматической сетке отсутствуют
некристаллографические оси 5-го и выше 6-го
порядков. Это приводит к сеткам следующей
симметрии.
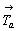 = =  , ,   90o 90o  120o 120o  60o (рис.
53, в). Косоугольный параллелограмм,
построенный на векторах 60o (рис.
53, в). Косоугольный параллелограмм,
построенный на векторах 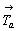 = =  , с углом , с углом   90o , хотя и является параллелограммом
повторяемости, но не может служить элементарной
ячейкой, так как симметрия полученной решетки
заставляет выбрать в качестве координатных
направлений векторы более высокой симметрии,
совпадающие с особыми направлениями такой
решетки - нормалями к плоскостям симметрии. Из рис. 53, в видно, что элементарная
ячейка в этом случае будет не примитивной, а
центрированной - с, т.е. ее группа симметрии - cmm2. 90o , хотя и является параллелограммом
повторяемости, но не может служить элементарной
ячейкой, так как симметрия полученной решетки
заставляет выбрать в качестве координатных
направлений векторы более высокой симметрии,
совпадающие с особыми направлениями такой
решетки - нормалями к плоскостям симметрии. Из рис. 53, в видно, что элементарная
ячейка в этом случае будет не примитивной, а
центрированной - с, т.е. ее группа симметрии - cmm2.
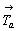 = =  , , = 90o (рис. 53,г) - p4mm. = 90o (рис. 53,г) - p4mm.
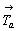 = =  , ,  = 120o (=60o ) (рис. 53, д)
- p6mm. = 120o (=60o ) (рис. 53, д)
- p6mm.
Задание угла  = 60o между исходными векторами не
изменит ни форму ячейки, ни симметрию
характеризуемой ею решетки - p6mm, так как угол
60o является дополнительным к углу 120o . = 60o между исходными векторами не
изменит ни форму ячейки, ни симметрию
характеризуемой ею решетки - p6mm, так как угол
60o является дополнительным к углу 120o .
На основании вышесказанного и из рис. 53 видно, что всякая
параллелограмматическая решетка (сетка)
обладает некоторыми обязательными элементами
симметрии: перпендикулярно к плоскости сетки
располагаются оси 2-го порядка (в проекции на
плоскость - "точки" 2-го порядка) либо как
самостоятельные элементы симметрии, либо как
составляющие осей высшего порядка; в решетках с
прямоугольными ячейками, а также в решетках с
осями высшего порядка обязательно имеются
зеркальные плоскости симметрии, линии
пересечения которых всегда совпадают с осями.
Плоскими аналогами точечных групп
симметрии, как и при выводе групп симметрии
одномерных узоров, могут служить группы
симметрии розеток (Cn и Cnv),
причем в данном случае, учитывая только что
выведенные группы симметрии плоских решеток,
сразу же отбираем 10 кристаллографических групп - 1,
2, 3, 4, 6, m, mm2, 3m, 4mm, 6mm (см. рис. 47,
с. 73) - и рассматриваем взаимодействие их
элементов симметрии с элементами симметрии
двухмерных решеток. Так же как в
вышерассмотренных одномерных группах, при таком
взаимодействии возникают новые - трансляционные
- элементы симметрии. В результате легко приходим
к 13 симморфным группам: p111, p112, pm11(= p1m1), cm11(=
c1m1), pmm2, cmm2, p4, p4mm, p3, p3m1, p31m, p6, p6mm и четырем несимморфным,
содержащим в качестве самостоятельных
трансляционные элементы симметрии: pb11(= p1a1), pma2(=
pbm2), pba2, p4bm (рис. 55 и 56).
C помощью выведенных 17 двухмерных
плоских групп симметрии
С помощью выведенных 17 двухмерных
плоских групп симметрии удобно описывать
отдельные сечения или проекции кристаллических
структур на координатные или другие плоскости,
которые обычно представляют собой сетки
(мозаики), построенные из многоугольников
(проекций полиэдров), в вершинах которых
расположены атомы или их группировки. С другой
стороны, если задать произвольную точку на
построенном графике одной из 17 плоских групп
симметрии и размножить ее всеми симметрическими
операциями группы, то получим систему
эквивалентных точек. Соединив ближайшие точки
прямыми линиями, не допуская при этом их
пересечения, получим разбиение плоскости на
многоугольники (плоские изогоны),
заполняющие всю плоскость без промежутков. В
каждой вершине плоского изогона сходятся
геометрически равные пучки ребер - сторон
многоугольников. Такие изогоны называются типическими.
Из всего многообразия полученных
таким образом мозаик [55] можно выделить 11 сеток - сеток
Кеплера [67], образованных правильными
многоугольниками (треугольниками, квадратами, 6-,
8-. 12-угольниками) или их комбинациями (рис.
57).
Существующие обозначения плоских
сеток символами Шлефли
указывают на число и тип правильных многоуголь-ников, сходящихся в каждом узле
рассматриваемой сетки. При этом арабская цифра 3
обозначает треугольник, 4 - квадрат и т.д.
Показатель степени указывает на количество
одинаковых, сходящихся в одной точке
многоугольников, сопри-касающихся
друг с другом своими сторонами. Например, сетка
из правильных шестиуголь-ников (графитовая
сетка, рис. 57) обозначается как 63, сетка 3636 образована
чередованием тре-угольников с шестиуголь-никами, сетка 34324
- последова-тельным чередованием в каждой
вершине треугольника, четырех-угольника, двух
треугольников и одного четырехугольника. Одна и
та же кристаллическая струк-тура
может быть составлена различными по
конфигурации сетками, расположенными
парал-лельно друг другу. Например, структуру
перовскита CaTiO3 можно
представить либо перпендикулярными к коорди-натным направлениям кубичес-кой структуры кислородными
сетками 44 двух типов (рис. 58, а, б),
либо чередующимися сетками 3636 и 36,
перпендикулярными осям 3-го порядка структуры (рис. 58, в).
Описанный выше прием - метод плоских
атомных сеток (структурных мозаик), часто
используемый при описании кристаллических
структур, позволяет выявлять те или иные
симметрийные особенности, а также сравнивать
фрагменты (атомные слои) различных структурных
типов.
|

