|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава V. Одномерные
группы симметрии - группы симметрии бордюров
В однородном дискретном
кристаллическом пространстве эквивалентные
точки расположены бесконечными параллельными
рядами. Поэтому изучение симметрии кристаллов
логично начать с рассмотрения симметрии
бесконечных одномерных регулярных построек -
атомных рядов, бордюров и т.п.
Обязательной операцией в бесконечной
одномерной регулярной постройке служит перенос -
трансляция. Каждая точка узора при этом
преобразовании повторяется в эквивалентных
позициях бесчисленное количество раз.
Ряд эквивалентных точек - узлов,
связанных операцией переноса, называется узловым рядом, который в
этом случае играет роль своеобразного
трансля-ционного элемента симметрии - одномерной
"решетки" (рис. 46). Характеристикой
узлово-го ряда служат величина и направление
вектора 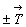 , называемого элементарным
переносом или периодом
идентичности и связывающего соседние
трансляционно идентичные узлы, расположенные на
минимальном конечном расстоянии друг от друга (amin).
Перемещение фигур при этом может происходить в
прямом и обратном направлении. , называемого элементарным
переносом или периодом
идентичности и связывающего соседние
трансляционно идентичные узлы, расположенные на
минимальном конечном расстоянии друг от друга (amin).
Перемещение фигур при этом может происходить в
прямом и обратном направлении.
Очевидно, что в одномерной "решетке"
не может быть промежуточных (дополнительных)
узлов. Такая "решетка" называется примитивной
и обозначается буквой "p". Ибо, если бы
дополнительный узел нашелся, то расстояние между
ним и какой-либо точкой оказалось бы меньше
расстояния a, принятого за кратчайшее между
идентичными точками.
Решетка, как и всякий трансляционный
элемент симметрии, с одной стороны, может
создавать бесконечный узор переносом конечной
фигуры в каком-либо направлении и, с другой -
передавать этому узору симметрию исходной
фигуры. Основываясь на симметрийном
принципе Кюри, заключающемся в том, что при
взаимодействии объекта (конечной фигуры) и
окружающей среды (решетки) в бесконечный
узор перейдут лишь общие для них элементы
симметрии, можно вывести все одномерные группы
симметрии. Для этого необходимо установить
симметрию одномерной решетки (узлового ряда) и
симметрию конечных фигур.
Симметрия
одномерной решетки - узлового ряда -
характеризуется предельной группой 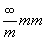 (группой симметрии неподвижного
цилиндра, см. c. 32). Ограничившись созданием
плоского одномерного одностороннего узора - бордюра,
следует сначала из объектов, описываемых 32
точечными группами симметрии, в качестве
размножаемых одномерной решеткой выбрать такие,
которые лишены "переворачивающих" элементов
симметрии, т.е. 10 односторонних розеток (рис. 47) с симметрией 1, 2, 3, 4, 6, m, mm2,
3m, 4mm, 6mm. Условие одномерности и
односторонности бесконеч-ного узора заставляет
отобрать из этих групп лишь четыре (1, 2, m,
mm2), лишенные осей высшего порядка,
перпендикулярных плоскости узора. Таким образом,
согласно принципу Кюри с одномерной решеткой
могут сочетаться лишь следующие элементы
симмет-рии: 1, 2, mx, my или их
комбинации, ибо только они присутствуют в
качестве элементов симметрии решетки и поэтому
могут быть переданы ею всему одномерному
плоскому одностороннему узору (бордюру). (группой симметрии неподвижного
цилиндра, см. c. 32). Ограничившись созданием
плоского одномерного одностороннего узора - бордюра,
следует сначала из объектов, описываемых 32
точечными группами симметрии, в качестве
размножаемых одномерной решеткой выбрать такие,
которые лишены "переворачивающих" элементов
симметрии, т.е. 10 односторонних розеток (рис. 47) с симметрией 1, 2, 3, 4, 6, m, mm2,
3m, 4mm, 6mm. Условие одномерности и
односторонности бесконеч-ного узора заставляет
отобрать из этих групп лишь четыре (1, 2, m,
mm2), лишенные осей высшего порядка,
перпендикулярных плоскости узора. Таким образом,
согласно принципу Кюри с одномерной решеткой
могут сочетаться лишь следующие элементы
симмет-рии: 1, 2, mx, my или их
комбинации, ибо только они присутствуют в
качестве элементов симметрии решетки и поэтому
могут быть переданы ею всему одномерному
плоскому одностороннему узору (бордюру).
В качестве примера можно рассмотреть
два бордюра, полученные переносом (трансляцией)
фигуры, обладающей зеркальной плоскостью m. В
группу симметрии первого бордюра (рис.
48, а) плоскость m перешла, так как она
совпала с одной из плоскостей симметрии
предельной группы 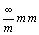 ,
характеризующей симметрию узлового ряда. Группа
симметрии 2-го бордюра (рис. 48, б)
этой плоскости не содержит, так как плоскость
такой ориентации в группе симметрии узлового
ряда отсутствует. ,
характеризующей симметрию узлового ряда. Группа
симметрии 2-го бордюра (рис. 48, б)
этой плоскости не содержит, так как плоскость
такой ориентации в группе симметрии узлового
ряда отсутствует.
?аким образом, легко выводятся симморфные
1 одномерные односторонние
группы симметрии: р111, р112, pm11, p1m1, pmm2. Из рис. 49 хорошо видно, что кроме
обозначенных в символе группы и присущих
конечным фигурам "подрешеточных" элементов
симметрии в результате их взаимодействия с
трансляцией решетки 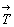 (трансляцией как элементом симметрии) возникают
результирующие дополнительные элементы
симметрии, чередующиеся с исходными либо
совпадающие с ними (см. с. 46 - 50).
(трансляцией как элементом симметрии) возникают
результирующие дополнительные элементы
симметрии, чередующиеся с исходными либо
совпадающие с ними (см. с. 46 - 50).
Действительно, добавление трансляции 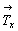 , перпендикулярной
плоскости mx, создает при
взаимодействии с ней новую чередующуюся с
исходной плоскость симметрии mx' ,
расположенную на расстоянии , перпендикулярной
плоскости mx, создает при
взаимодействии с ней новую чередующуюся с
исходной плоскость симметрии mx' ,
расположенную на расстоянии 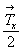 . Кроме того, при взаимодействии . Кроме того, при взаимодействии 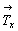 с my возникает
совпадающая с my плоскость скользящего
отражения ay с трансляционной
компонентой с my возникает
совпадающая с my плоскость скользящего
отражения ay с трансляционной
компонентой 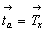 . Эти
"дополнительные" элементы симметрии,
естественно, как и каждый член
кристаллографической группы симметрии, имеют
право на самостоятельное существование. Замена в
симморфных группах макроэлементов симметрии на
возможный в одномерном одностороннем узоре
трансляционный элемент симметрии, в данном
случае ay, приведет еще к двум группам: p1a1
и pma2 (рис. 49). . Эти
"дополнительные" элементы симметрии,
естественно, как и каждый член
кристаллографической группы симметрии, имеют
право на самостоятельное существование. Замена в
симморфных группах макроэлементов симметрии на
возможный в одномерном одностороннем узоре
трансляционный элемент симметрии, в данном
случае ay, приведет еще к двум группам: p1a1
и pma2 (рис. 49).
Итак, получено 7 одномерных групп
симметрии - групп симметрии бордюров, варианты
конкретной реализации которых представлены на рис. 50.
Бордюры можно считать частным случаем лент
- двухсторонних, бесконечных в одном направлении
периодических построек, обладающих
"переворачивающими" элементами симметрии, т.е.
такими, которые совмещают обе стороны ленты и
располагаются в плоскости самой ленты. Это
плоскости симметрии, совпадающие с плоскостью
ленты, и винтовая ось 2-го порядка, совпадающая с
узловым рядом.
Увеличение списка операций симметрии
добавляет к перечисленным выше семи группам
симметрии бордюров еще 24 группы симметрии лент
[55].
Постройки, бесконечные в одном
направлении, содержащие кроме трансляции
совпадающие с ней поворотные,
зеркально-поворотные и винтовые оси симметрии
любого порядка, называют стержнями, примером
которых служат трубы, винты, цепи и т.п.
Естественно, что добавление новых элементов
симметрии приведет к большему количеству групп
симметрии стержней по сравнению с количеством
групп симметрии бордюров и лент (рис.
51).
|

