|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.10. Взаимодействие оси 4-го порядка и
перпендикулярной к ней плоскости симметрии
Результатом взаимодействия простых
операций симметрии - поворота вокруг оси 4-го
порядка (4z) с последующим отражением в
перпендикулярной к ней плоскости (mz) - будет
зеркально-поворотная или соответствующая ей
инверсионная ось 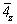 ,
особая точка которой совпадает с истинным
центром инверсии - результатом взаимодействия
оси 2 = 42 и перпендикулярной ей
плоскости. И хотя особое направление в группе
представлено совпадающими поворотной и
инверсионной осями 4-го порядка, его
характеризуют в символе группы простой осью,
оставляя ось ,
особая точка которой совпадает с истинным
центром инверсии - результатом взаимодействия
оси 2 = 42 и перпендикулярной ей
плоскости. И хотя особое направление в группе
представлено совпадающими поворотной и
инверсионной осями 4-го порядка, его
характеризуют в символе группы простой осью,
оставляя ось 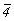 в скрытом
виде. Если исходные элементы симметрии (4 .
m в скрытом
виде. Если исходные элементы симметрии (4 .
m )
имеют трансляционные составляющие, т.е. ось 4-го
порядка винтовая, а плоскость, ей
перпендикулярная, является плоскостью
скользящего отражения, то каждая из их
трансляционных компонент будет
взаимодействовать с возникшей осью )
имеют трансляционные составляющие, т.е. ось 4-го
порядка винтовая, а плоскость, ей
перпендикулярная, является плоскостью
скользящего отражения, то каждая из их
трансляционных компонент будет
взаимодействовать с возникшей осью 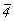 по-разному. Горизонтальная
трансляционная компонента плоскости
скользящего отражения перенесет результирующую
ось по-разному. Горизонтальная
трансляционная компонента плоскости
скользящего отражения перенесет результирующую
ось 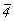 в центр
построенного на ней квадрата (см. с. 56). Особая же
точка инверсионной оси окажется смещенной на
середину вертикальной составляющей винтовой оси
4-го порядка. в центр
построенного на ней квадрата (см. с. 56). Особая же
точка инверсионной оси окажется смещенной на
середину вертикальной составляющей винтовой оси
4-го порядка.
Например, представив действие оси 42
и перпендикулярной к ней плоскости симметрии nz
составляющими их симметрическими операциями: 42
. nz = (4 . 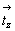 ) . (mz
. ) . (mz
. 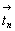 ) (где ) (где 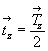 ) (рис. 45),
увидим, что взаимодействие операций 4 .
m ) (рис. 45),
увидим, что взаимодействие операций 4 .
m даст
инверсионную ось даст
инверсионную ось 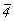 ,
которая под действием горизонтального вектора ,
которая под действием горизонтального вектора 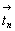 ?удет перенесена в центр
построенного на нем квадрата; особая же точка
этой оси окажется ?еренесенной вектором + ?удет перенесена в центр
построенного на нем квадрата; особая же точка
этой оси окажется ?еренесенной вектором + 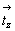 на его середину, т.е. на на его середину, т.е. на 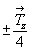 от уровня заданной
плоскости nz. Поскольку трансляционные
векторы клиноплос-кости n направлены
одновременно вдоль каждой из диагоналей
горизонтальной грани элементарной ячейки в
противоположные стороны, ось 42
окажется окруженной четырьмя осями от уровня заданной
плоскости nz. Поскольку трансляционные
векторы клиноплос-кости n направлены
одновременно вдоль каждой из диагоналей
горизонтальной грани элементарной ячейки в
противоположные стороны, ось 42
окажется окруженной четырьмя осями 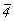 в центрах всех четырех квадратов,
построенных на + в центрах всех четырех квадратов,
построенных на + 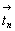 (см. с. 56). При этом верти-кальные компоненты оси 42
, направленные в противоположные стороны (+
(см. с. 56). При этом верти-кальные компоненты оси 42
, направленные в противоположные стороны (+ 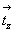 ), обусловят появление
особых точек инверсионной оси на высоте как ), обусловят появление
особых точек инверсионной оси на высоте как 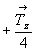 , так и , так и 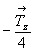 , что вполне объясняется периодичностью
этих точек через , что вполне объясняется периодичностью
этих точек через 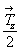 . В
этом случае последовательность проводимых
симметрических операций не скажется на конечном
результате. . В
этом случае последовательность проводимых
симметрических операций не скажется на конечном
результате.
Каждая из поворотных осей 2-го порядка: 2
= 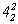 и 2 = и 2 = 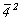 , взаимодействуя с
перпендикулярной к ней плоскостью n,
обусловит появление на уровне этой плоскости
центров инверсии, смещенных из точек пересечения
оси с плоскостью на середину вектора , взаимодействуя с
перпендикулярной к ней плоскостью n,
обусловит появление на уровне этой плоскости
центров инверсии, смещенных из точек пересечения
оси с плоскостью на середину вектора 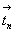 . .
Однако в случае взаимодействия более
сложных элементов симметрии, например 41
. a , с трансляционными векторами в
1/4 координатных трансляций при определении
позиции особой точки оси , с трансляционными векторами в
1/4 координатных трансляций при определении
позиции особой точки оси 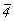 необходимо учитывать не только
взаимодействие, но и действие самих операций
симметрии друг на друга [27] (см. с. 154). необходимо учитывать не только
взаимодействие, но и действие самих операций
симметрии друг на друга [27] (см. с. 154).
|

