|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.9. Взаимодействие двух плоскостей
симметрии, расположенных под углом 45o друг
к другу
При рассмотрении частного случае
теоремы Эйлера, а именно: взаимодействия
зеркальных плоскостей симметрии (см. с. 18) - было
доказано, что последовательно проведенные
операции отражения в плоскостях m и m' ,
расположенных под углом 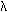 , равносильны повороту вокруг
результирующей оси, порядок которой зависит от
угла , равносильны повороту вокруг
результирующей оси, порядок которой зависит от
угла 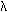 ( ( = 2 = 2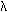 ). Однако при
доказательстве этой теоремы не учитывалась
очередность выстроенных симметрических
операций. А ведь именно от этого зависят характер
поворота вокруг результирующей оси и ее
положение. ). Однако при
доказательстве этой теоремы не учитывалась
очередность выстроенных симметрических
операций. А ведь именно от этого зависят характер
поворота вокруг результирующей оси и ее
положение.
В случае отсутствия у порождающих
плоскостей симметрии трансляционных компонент,
перпендикулярных возникшей оси 4-го порядка, ее
положение четко фиксируется линией пересечения
исходных плоскостей. Однако направление
поворота вокруг результирующей оси будет
зависеть от того, в каком порядке осуществляются
операции симметрии. Если первой операцией
является отражение в плоскости my (точка
1 перейдет в точку 2) (рис. 43, а), а
второй - отражение в md (точка 2 перейдет
в точку 3), то исходная и конечная фигуры
совместятся поворотом вокруг возникшей оси 4z
на угол 90o против часовой стрелки. Если же
сначала осуществить отражение в плоскости md
, а затем в my (рис. 43, б),
то результирующий поворот будет направлен в
противоположную сторону (по часовой стрелке): от
плоскости первого отражения к плоскости второго
отражения [19], т.е. получим различные
результирующие повороты: my . md
= 41, md . my = 4-1.
Если одна (или обе) из исходных
плоскостей симметрии имеет горизонтальную
трансляционную составляющую, то образовавшаяся
ось 4-го порядка за счет взаимодействия с этим
вектором будет перенесена в центр построенного
на нем квадрата, при этом квадрат будет
расположен от этого вектора в сторону
направления вращения вокруг возникшей оси (см. с.
56). Однако при выявлении положения
результирующей оси следует также учитывать
последовательность проводимых симметрических
операций, в противном случае могут быть получены
ошибочные результаты. Например, ошибочно
предположив, что возникшая поворот-ная ось 4z
(у взаимодей-ствующих плоскостей отсутствуют
вертикаль-ные трансляционные компоненты!)
попадет в квадрат, центр которого располагается
на диаго-нальной плоскости md (рис. 44, а), увидим, что результатом
взаимодей-ствия оси 4 и md будет
появление координатной плоскости my,
чередую-щейся с исходной ay, что
невозможно в Р-решетке (см. с. 88).
В действительности же результатом
двух последовательных отражений в плоскостях ay
и md будет ось 4z, расположенная
в центре квадрата, построенного не на векторе 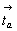 (рис. 44, а),
а на векторе ему энантиоморфном (рис. 44, а),
а на векторе ему энантиоморфном 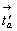 , так как операция отражения в
плоскости md изменит направление
вектора , так как операция отражения в
плоскости md изменит направление
вектора 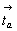 . Смена
последовательности отражений на обратную -
вначале в плоскости md , а затем в ay
- поменяет и положение результирующей оси (рис. 44, б): она окажется в центре
квадрата, построенного на исходном векторе . Смена
последовательности отражений на обратную -
вначале в плоскости md , а затем в ay
- поменяет и положение результирующей оси (рис. 44, б): она окажется в центре
квадрата, построенного на исходном векторе 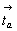 , ибо последовательность
операций симметрии (md . ay =
md . my . , ибо последовательность
операций симметрии (md . ay =
md . my . 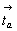 ) такова, что этот вектор не
подвержен действию других симметрических
операций. В итоге видим, что ось 4-го порядка
располагается по ту сторону от трансляционного
вектора, куда направлен результирующий поворот,
т.е. от плоскости первого отражения ко второй.
Изменение направления трансляционного вектора + ) такова, что этот вектор не
подвержен действию других симметрических
операций. В итоге видим, что ось 4-го порядка
располагается по ту сторону от трансляционного
вектора, куда направлен результирующий поворот,
т.е. от плоскости первого отражения ко второй.
Изменение направления трансляционного вектора +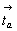 на обратный - на обратный - 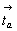 к новым положениям оси 4z
не приведет. к новым положениям оси 4z
не приведет.
|

