|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.3. Графическое представление
пространственных групп моноклинной сингонии
Графики пространственных групп
существенно облегчают понимание
пространственного расположения элементов
симметрии и расположение правильных систем
точек (см. с. 232), а также определение их
характеристик. Особенно это касается графиков
моноклинной сингонии, где два сечения
элементарной ячейки прямоугольны, а одно,
перпендикулярное единственному особому
направлению, оказывается косоугольным.
Прежде всего следует остановиться на новых
условных обозначениях элементов симметрии,
используемых в графиках пространственных групп
низшей категории. Помимо вертикальных элементов
симметрии - осей 2-го порядка и плоскостей, с
обозначениями которых мы уже знакомы (см. с. 5, 47,
49), а также центров инверсии, обозначаемых на
графиках пространственных групп маленьким
кружочком (o ), в графиках моноклинных групп
появляются горизонтальные элементы симметрии,
обозначения которых выносятся за пределы
контура элементарной ячейки: поворотные оси 2-го
порядка изображаются обычно стрелкой (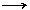 ),
винтовые оси 21 - также стрелкой, но лишь с
одним "крылом"( ),
винтовые оси 21 - также стрелкой, но лишь с
одним "крылом"(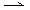 ). Обозначения горизонтальных
плоскостей симметрии (m, a, b, n, d
соответственно) выносятся в верхний левый угол
графика. Дробное число, стоящее рядом со знаком
элемента симметрии, указывает на его высоту
относительно нулевого уровня (z = 0) элементарной
ячейки. ). Обозначения горизонтальных
плоскостей симметрии (m, a, b, n, d
соответственно) выносятся в верхний левый угол
графика. Дробное число, стоящее рядом со знаком
элемента симметрии, указывает на его высоту
относительно нулевого уровня (z = 0) элементарной
ячейки.
Для того чтобы представить графики
пространственных групп моноклинной сингонии в
стандартном для данной группы аспекте - в
классической установке, строится проекция на
плоскость, перпендикулярную оси Z ячейки, т.е.
проекция на плоскость xy (рис. 68,
а). Такую прямоугольную проекцию полезно
сопроводить графиком группы, спроектированной
на плоскость косоугольной грани xz, т.е. в
новой установке, где угол моноклинности
оказывается не искаженным (рис. 68,
б).
При построении графиков
голоэдрических моноклинных групп вначале на них
наносятся "подрешеточные" элементы симметрии,
принятые за порождающие: оси 2-го порядка и
перпендикулярные к ним плоскости симметрии.
Результатом взаимодействия данных плоскостей
симметрии и осей 2-го порядка с перпендикулярными
к ним трансляциями решетки (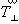 ) являются плоскости (или соответственно
оси) симметрии того же наименования,
параллельные исходным и отстоящие от них на ) являются плоскости (или соответственно
оси) симметрии того же наименования,
параллельные исходным и отстоящие от них на 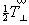 ( см рис. 25 и 69), т.е. появляется периодичность в
расположении одноименных элементов симметрии
(плоскостей или осей 2-го порядка) через ( см рис. 25 и 69), т.е. появляется периодичность в
расположении одноименных элементов симметрии
(плоскостей или осей 2-го порядка) через 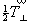 (см. с. 49 и 52). Чередование
разноименных плоскостей симметрии (например, c(n)
или осей 2-го порядка (2(21)) через (см. с. 49 и 52). Чередование
разноименных плоскостей симметрии (например, c(n)
или осей 2-го порядка (2(21)) через 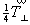 (рис. 69)
объясняется присутствием в рассматриваемой
группе (рис. 69)
объясняется присутствием в рассматриваемой
группе 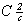 дополнительного, центрирующего грань С
элементарной ячейки трансляционного вектора
дополнительного, центрирующего грань С
элементарной ячейки трансляционного вектора 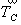 , расположенного косо и к
исходной плоскости с, и к оси 2. Одна из
координатных компонент, на которые
раскладывается вектор , расположенного косо и к
исходной плоскости с, и к оси 2. Одна из
координатных компонент, на которые
раскладывается вектор 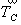 ,
- параллельная исходному элементу симметрии -
изменит его наименование (в данном случае
плоскость с, получив дополнительное
скольжение, превратится в клиноплоскость n, а
ось 2 - в 21), вторая компонента,
перпендикулярная производному элементу
симметрии (n или 21), перенесет их на
свою середину, обусловив этим чередование
плоскостей с(n) вдоль координатного
направления Z и 2(21) вдоль оси X (рис. 69). ,
- параллельная исходному элементу симметрии -
изменит его наименование (в данном случае
плоскость с, получив дополнительное
скольжение, превратится в клиноплоскость n, а
ось 2 - в 21), вторая компонента,
перпендикулярная производному элементу
симметрии (n или 21), перенесет их на
свою середину, обусловив этим чередование
плоскостей с(n) вдоль координатного
направления Z и 2(21) вдоль оси X (рис. 69).
В результате взаимодействия плоскости
симметрии и перпендикулярной к ней оси 2-го
порядка возникает обязательный для
голоэдрических групп центр инверсии. Однако если
в пр. гр. 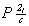 (см. рис.
68) центр инверсии оказывается сдвинутым
трансляционной компонентой винтовой оси 21
( (см. рис.
68) центр инверсии оказывается сдвинутым
трансляционной компонентой винтовой оси 21
(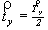 ) из точки
пересечения оси и плоскости на ее (компоненты)
середину, т.е. на ) из точки
пересечения оси и плоскости на ее (компоненты)
середину, т.е. на 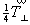 , и как
бы существует самостоятельно, то в пр. гр. , и как
бы существует самостоятельно, то в пр. гр. 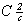 за счет присутствия
дополнительного вектора за счет присутствия
дополнительного вектора 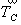 , а следовательно, появления как бы
"вложенных" плоскостей симметрии (n) все
центры (исходные и производные) на графике
оказываются локализованными на плоскостях
скользящего отражения, сохраняя при этом
симметрию позиции , а следовательно, появления как бы
"вложенных" плоскостей симметрии (n) все
центры (исходные и производные) на графике
оказываются локализованными на плоскостях
скользящего отражения, сохраняя при этом
симметрию позиции 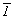 . .
Заключительным этапом вычерчивания
графика пространственной группы является выбор
начала координат элементарной ячейки. По
принятому в Интернациональных Таблицах [73, 74]
стандарту в качестве начала координат самую
симметричную ( с максимальной точечной
симметрией) и самую неподвижную (жестко
фиксированную элементами симметрии) точку (т.е.точку
с минимальным числом степеней свободы -
минимальным количеством направлений, в которых
она может смещаться, не нарушая своей симметрии).
Выбор начала координат в моноклинных
голоэдрических группах не вызывает затруднений,
так как центры инверсии четко фиксируют позиции
без степеней свободы (см. рис. 68).
Причем если в примитивных группах и группе 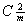 такой выбор бесспорен - в
позиции такой выбор бесспорен - в
позиции 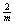 с максимальной
величиной симметрии (равной 4), то в группе с максимальной
величиной симметрии (равной 4), то в группе 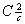 из двух систем
топологически одинаковых центров инверсии в
Интернациональных таблицах традиционно
предпочтен центр инверсии, расположенный в
исходной плоскости с (см. рис. 69),
с такой же величиной симметрии (равной 2), как и в
плоскости n. из двух систем
топологически одинаковых центров инверсии в
Интернациональных таблицах традиционно
предпочтен центр инверсии, расположенный в
исходной плоскости с (см. рис. 69),
с такой же величиной симметрии (равной 2), как и в
плоскости n.
|

