|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.2. Вывод
пространственных групп моноклинной сингонии
Взяв за основу точечные группы
моноклинной сингонии: голоэдрическую 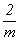 и гемиэдрические 2 и m,
а также возможные моноклинные решетки Браве - Р
и С (имеется в виду минералогическая
ориентация моноклинных групп, где единственное
особое направление совмещено с горизонтальной
координатной осью Y), можно вывести все
пространственные группы данной сингонии, при
этом фактически ограничившись выводом лишь
голоэдрических, получив остальные в качестве их
подгрупп. и гемиэдрические 2 и m,
а также возможные моноклинные решетки Браве - Р
и С (имеется в виду минералогическая
ориентация моноклинных групп, где единственное
особое направление совмещено с горизонтальной
координатной осью Y), можно вывести все
пространственные группы данной сингонии, при
этом фактически ограничившись выводом лишь
голоэдрических, получив остальные в качестве их
подгрупп.
При выводе групп моноклинной
голоэдрии С2h = 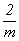 из трех присутствующих элементов
симметрии: из трех присутствующих элементов
симметрии: 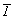 , m и 2
- порождающими удобно считать ось 2-го порядка и
перпендикулярную к ней плоскость симметрии. И
тогда, учитывая, что для каждого из трех знаков
символа группы имеются две возможности: решетки Р
и С, оси 2 и 21, плоскости
зеркальные (m) и скользящего отражения, легко
получить четыре примитивные и две
базоцентрированные голоэдрические группы. , m и 2
- порождающими удобно считать ось 2-го порядка и
перпендикулярную к ней плоскость симметрии. И
тогда, учитывая, что для каждого из трех знаков
символа группы имеются две возможности: решетки Р
и С, оси 2 и 21, плоскости
зеркальные (m) и скользящего отражения, легко
получить четыре примитивные и две
базоцентрированные голоэдрические группы.
Действительно, в присутствии лишь
одного особого направления исчезает возможность
принудительного фиксирования двух координатных
направлений, а следовательно, и необходимость
рассмотрения центрировки косоугольной грани
элементарной ячейки, ибо любая ее центрировка
приведет к появлению более короткого
трансляционного вектора и соответственно к
возможности выбора Р-ячейки меньшего
размера. Оси 2 и 21, так же как и
перпендикулярные к ним плоскости, в Р-ячейке
из-за отсутствия косо расположенных к оси Y
трансляционных векторов становятся
независимыми. Поскольку выбор двух координатных
осей в моноклинной ячейке в плоскости,
перпендикулярной единственному особому
направлению, произволен, то трансляционная
компонента плоскости скользящего отражения
может оказаться по-разному ориентированной
относительно выбранного координатного репера.
Поэтому плоскость скользящего отражения может
получить в зависимости от ориентации ее вектора
разные наименования: a, b, c, n или d (см. рис. 66, 67). В
Интернациональных таблицах [71 - 73] по традиции
предпочтение отдано плоскости скользящего
отражения с с трансляционным вектором, часто
совпадающим с удлинением кристалла.
Пространственные группы с Р-решеткой
С учетом вышесказанного получим
четыре пространственные группы с Р-решеткой:
симморфную 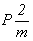 ,
гемисимморфные ,
гемисимморфные 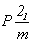 и и 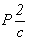 и асимморфную и асимморфную 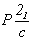 . Однако такая краткая
запись не указывает на установку данной
пространственной группы - классическую
(минералогическую) или новую (рациональную) (см. c.
90), т.е. на то, с какой координатной осью совмещено
единственное особое направление. Этого
недостатка лишена развернутая запись
пространственной группы с использованием на
соответствующих позициях символа единиц - осей
1-го порядка (рис. 64, а). Часто
международный символ (символ Германа -
Могена) пространственной группы
сопровождается ее обозначением по Шенфлису,
играющим роль своеобразного "ключа". Например, . Однако такая краткая
запись не указывает на установку данной
пространственной группы - классическую
(минералогическую) или новую (рациональную) (см. c.
90), т.е. на то, с какой координатной осью совмещено
единственное особое направление. Этого
недостатка лишена развернутая запись
пространственной группы с использованием на
соответствующих позициях символа единиц - осей
1-го порядка (рис. 64, а). Часто
международный символ (символ Германа -
Могена) пространственной группы
сопровождается ее обозначением по Шенфлису,
играющим роль своеобразного "ключа". Например, 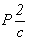 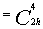 ,
где верхний индекс, указывая на определенную
пространственную группу, никакой другой
смысловой нагрузки, кроме ее порядкового номера,
не несет. ,
где верхний индекс, указывая на определенную
пространственную группу, никакой другой
смысловой нагрузки, кроме ее порядкового номера,
не несет.
Итак, символы перечисленных
пространственных групп запишутся следующим
образом :
| Обозначения Шенфлиса |
Классическая установка |
Рациональная установка |
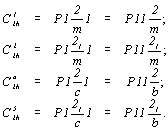 |
Пространственные группы с С-решеткой
В базоцентрированных группах вектор 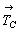 лежит в плоскости грани С
и расположен косо к единственному особому
направлению, выбранному в качестве координатной
оси Y элементарной С-ячейки (минералогическая
установка). Каждая из координатных компонент
вектора лежит в плоскости грани С
и расположен косо к единственному особому
направлению, выбранному в качестве координатной
оси Y элементарной С-ячейки (минералогическая
установка). Каждая из координатных компонент
вектора 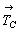 = = 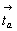 + + 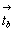 (рис. 64, б), на которые можно его
разложить по правилу паллелограмма, будет
взаимодействовать с "подрешеточными"
элементами симметрии - плоскостью и
перпендикулярной ей осью 2-го порядка -
по-разному. Компонента (рис. 64, б), на которые можно его
разложить по правилу паллелограмма, будет
взаимодействовать с "подрешеточными"
элементами симметрии - плоскостью и
перпендикулярной ей осью 2-го порядка -
по-разному. Компонента 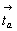 ,
параллельная плоскости симметрии, вольется в нее
как дополнительное скольжение, изменив тем самым
ее характер, вторая же компонента ,
параллельная плоскости симметрии, вольется в нее
как дополнительное скольжение, изменив тем самым
ее характер, вторая же компонента 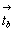 , перпендикулярная производной
плоскости, перенесет ее на свою середину (см. с. 50),
т.е. на , перпендикулярная производной
плоскости, перенесет ее на свою середину (см. с. 50),
т.е. на 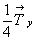 , обусловив
тем самым чередование в этом направлении
плоскостей разного наименования: , обусловив
тем самым чередование в этом направлении
плоскостей разного наименования:
my . 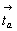 = ay, ay . = ay, ay . 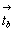 --> my (ay); --> my (ay);
сy . 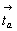 = my . = my . 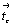 . . 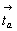 = ny , ny . = ny , ny . 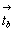 --> cy (ny)
(рис. 64, б). --> cy (ny)
(рис. 64, б).
Те же самые компоненты (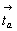 и и 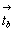 )
заставят поворотные оси 2 чередоваться с
винтовыми 21 в плоскости центрированной
грани: )
заставят поворотные оси 2 чередоваться с
винтовыми 21 в плоскости центрированной
грани:
2y . 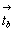 = 21(y), 21(y) . = 21(y), 21(y) . 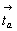 --> 2y(21(y)). --> 2y(21(y)).
Указанные чередования могут быть
отмечены в развернутых символах групп: 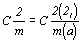 и и 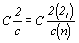 . .
В итоге, с одной стороны, все четыре
примитивные группы сольются в одну
базоцентрированную 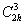 , с
другой - две из них дадут группу , с
другой - две из них дадут группу 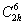 : :
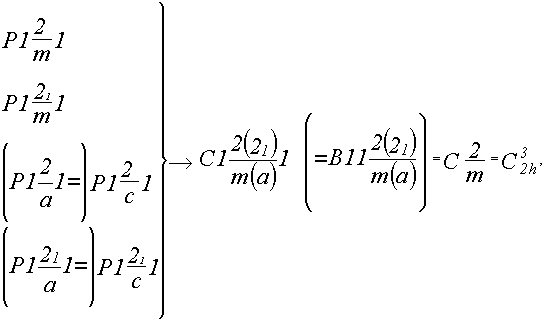
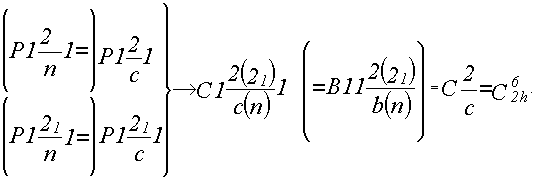
Вывод моноклинных гемиэдрических
групп легко осуществить, либо задавая на
единственной позиции символа возможные в
моноклинной ячейке разновидности осей 2-го
порядка или плоскостей симметрии, либо путем
отбрасывания из голоэдрических групп "лишних"
элементов симметрии. При этом надо иметь в виду,
что в символах всех групп моноклинной голоэдрии
в скрытом виде находится центр инверсии,
являющийся произведением оси 2-го порядка и
перпендикулярной к ней плоскости симметрии.
Поэтому, отбрасывая центр инверсии, мы
одновременно должны убрать либо плоскость
симметрии, либо ось 2-го порядка. В первом случае
придем к трем пространственным группам,
подчиненным точечной С2, во втором - к
четырем группам Сs:
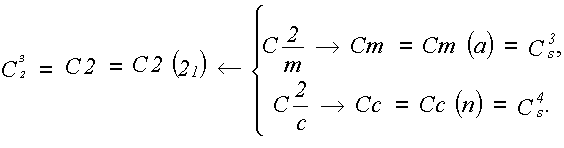
Следует также подчеркнуть, что в
группах Cm и Сс плоскости m и с независимы.
Присутствие же вектора 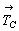 ,
косо расположенного к заданной плоскости, задает
чередование плоскостей m(a) и c(n). Этому же
вектору в группе С2 обязано чередование осей 2(21). ,
косо расположенного к заданной плоскости, задает
чередование плоскостей m(a) и c(n). Этому же
вектору в группе С2 обязано чередование осей 2(21).
Поскольку в моноклинных кристаллах
отсутствие особых направлений в плоскости
симметрии допускает произвольный выбор
координатных осей - ребер a и b -
элементарной ячейки, исследователь часто
сталкивается с неоднозначностью описания той
или иной моноклинной структуры. Действительно,
различный выбор координатных направлений, часто
с нарушением принципа минимальности объема
элементарной ячейки, приводит к тому, что
трансляционные компоненты плоскостей
скользящего отражения оказываются по-разному
ориентированными относительно координатного
репера, что приводит к изменению их наименования.
Трудность в установлении ориентации
элементарной ячейки появляется еще и в том
случае, если исследователем не указано
наименование угла моноклинности ( или или  ), т.е. тип установки
кристалла (классический или рациональный). В этом
случае по символу, если отсутствуют единицы на
его свободных позициях, часто нельзя судить об
установке моноклин-ного кристалла. Например,
символ ), т.е. тип установки
кристалла (классический или рациональный). В этом
случае по символу, если отсутствуют единицы на
его свободных позициях, часто нельзя судить об
установке моноклин-ного кристалла. Например,
символ 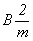 , с одной
стороны, представ-ляет пространственную группу , с одной
стороны, представ-ляет пространственную группу 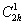 в минералогической
установке, сводимую к в минералогической
установке, сводимую к 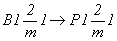 (рис. 65, а), и, с другой -
пространственную группу (рис. 65, а), и, с другой -
пространственную группу 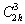 - наиболее распространенную ее установку - наиболее распространенную ее установку 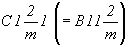 (рис. 65, б). (рис. 65, б).
Как видно, при таком написании группы 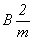 без дополнительных
указаний (символа Шенфлиса, наименования угла
моноклинности, присутствия единиц на "пустых"
позициях международного символа) группы без дополнительных
указаний (символа Шенфлиса, наименования угла
моноклинности, присутствия единиц на "пустых"
позициях международного символа) группы 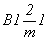 и и 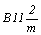 неразличимы. неразличимы.
Рассмотрим некоторые часто
встречающиеся аспекты пространственных групп
моноклинной сингонии (в скобках указаны
обозначения групп в рациональной установке):
1. 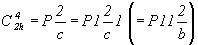 (рис. 66, а). (рис. 66, а).
Трансляционная компонента плоскости с
направлена вдоль оси Z. Изменение наименования
осей X и Z приведет к тому, что трансляционная
компонента плоскости скользящего отражения
окажется ориентированной параллельно оси X и
пространственная группа в этом случае запишется
как 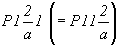 (рис. 66,
б). При ином выборе координатных направлений (рис. 66,в) трансляционная компонента
плоскости симметрии окажется направленной в
центр грани (010) (или (001) для иной установки), т.е.
станет компонентой клиноплоскости n, а
следовательно, пространственная группа
запишется как (рис. 66,
б). При ином выборе координатных направлений (рис. 66,в) трансляционная компонента
плоскости симметрии окажется направленной в
центр грани (010) (или (001) для иной установки), т.е.
станет компонентой клиноплоскости n, а
следовательно, пространственная группа
запишется как 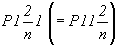 , либо
компонентой клиноплоскости d (рис.
66, г), пр. гр. , либо
компонентой клиноплоскости d (рис.
66, г), пр. гр. 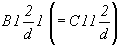 .
Центрированные же ячейки (рис. 66, д,
е) будут характеризоваться
пространственными группами .
Центрированные же ячейки (рис. 66, д,
е) будут характеризоваться
пространственными группами 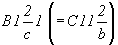 и и 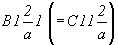 соответственно.
соответственно.
Таким образом, некоторая свобода в
выборе координатных направлений привела к
нескольким аспектам пр. гр. 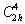 : : 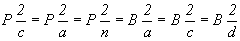 в классической
установке и соответственно к в классической
установке и соответственно к 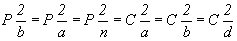 - в новой. - в новой.
2. 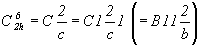 (рис. 67, а). (рис. 67, а).
Трансляционная компонента плоскости с
направлена вдоль оси Z. Перемена наименований
осей X и Z приведет к изменению обозначений
трансляционной компоненты 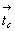 на на 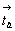 , и
следовательно, к пространственной группе , и
следовательно, к пространственной группе 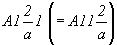 (рис. 67, б). (рис. 67, б).
При ином выборе координатных
направлений трансляционная компонента
плоскости скользящего отражения направлена в
центр грани (010), т.е. становится компонентой либо
клиноплоскости n (рис. 67, в) -
пространственная группа в этом случае запишется
как 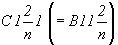 , либо
клиноплоскости d (рис. 67, г) -
пр. гр. , либо
клиноплоскости d (рис. 67, г) -
пр. гр. 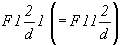 . Представление
заданной решетки в I-аспекте приведет к
пространственным группам . Представление
заданной решетки в I-аспекте приведет к
пространственным группам 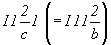 (рис. 67, д) и (рис. 67, д) и 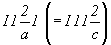 (рис. 67, е). (рис. 67, е).
Таким образом, пространственная
группа 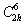 может быть
представлена кроме наиболее распространенного
аспекта может быть
представлена кроме наиболее распространенного
аспекта 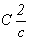 аспектами аспектами 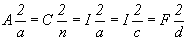 в классической и
соответственно в классической и
соответственно 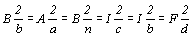 в
новой установке 1. в
новой установке 1.
|

