|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.5. Графическое представление
пространственных групп ромбической сингонии
Прежде чем начать строить график
пространственной группы, следует, задав значения
трансляционных координатных векторов, лежащих в
плоскости чертежа, изобразить в масштабе
проекцию элементарной ячейки в соответствующей
установке и далее при вычерчивании гемиморфных
пространственных групп, посчитав в качестве
порождающих элементов симметрии записанные в
символе плоскости, изобразить их на
соответствующих позициях. Если решетка
примитивная, то заданные плоскости симметрии
будут взаимодействовать лишь с
перпендикулярными к ним координатными
трансляционными векторами 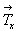 , ,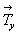 и и 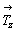 и между собой. В результате
взаимодействия плоскости с вектором,
перпендикулярным к ней, возникнет плоскость того
же наименования на его середине (см. с. 49). Это
обусловит периодичность в расположении
одноименных плоскостей, равную половине
координатных трансляций ( и между собой. В результате
взаимодействия плоскости с вектором,
перпендикулярным к ней, возникнет плоскость того
же наименования на его середине (см. с. 49). Это
обусловит периодичность в расположении
одноименных плоскостей, равную половине
координатных трансляций (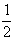 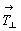 ). В качестве
порожденных элементов симметрии возникнут
центры инверсии и оси 2-го порядка, характер и
положение которых будут зависеть от типа
пересекающихся порождающих плоскостей
симметрии (см. с. 59). ). В качестве
порожденных элементов симметрии возникнут
центры инверсии и оси 2-го порядка, характер и
положение которых будут зависеть от типа
пересекающихся порождающих плоскостей
симметрии (см. с. 59).
Задав вначале лишь плоскости первых
двух позиций символа и получив результирующую
ось 2-го порядка, мы, таким образом, вычертим
график одной из гемиморфных групп. Последующее
взаимодействие элементов симметрии гемиморфной
группы с заданной горизонтальной плоскостью
обусловит возникновение целой серии
дополнительных элементов симметрии, характерных
для голоэдрических пространственных групп.
В качестве примера построим график
пространственной группы Pbcn в ее
нестандартном аспекте Pnca (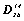 ). ).
1. Вычертив в масштабе элементарную
ячейку (a b, b,  = 90o ), нанесем на график (рис. 76, 1) записанные в символе
вертикальные плоскости nx и сy. = 90o ), нанесем на график (рис. 76, 1) записанные в символе
вертикальные плоскости nx и сy.
2. Размножим заданные плоскости
перпендикулярными к ним координатными
трансляционными векторами 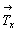 и и 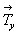 . Таким
образом, элементарная ячейка окажется
оконтуренной заданными плоскостями (рис.
76, 2). . Таким
образом, элементарная ячейка окажется
оконтуренной заданными плоскостями (рис.
76, 2).
3. За счет взаимодействий исходных
плоскостей с векторами 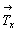 и
и 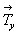 появятся плоскости
такого же наименования на их серединах (рис. 76, 3): появятся плоскости
такого же наименования на их серединах (рис. 76, 3):
nx . 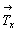 --> nx на
расстоянии --> nx на
расстоянии 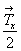 , ,
сy . 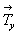 --> сy на расстоянии --> сy на расстоянии 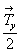 . .
4. Взаимодействие двух взаимно
перпендикулярных плоскостей nx.
сy приведет в появлению
результирующей оси 2-го порядка, характер которой
будет определяться вертикальными
трансляционными составляющими
взаимодействующих плоскостей симметрии.
Представив каждую из плоскостей скользящего
отражения составляющими их симметрическими
операциями: 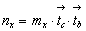 , , 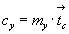 , увидим, что векторы , увидим, что векторы 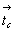 обеих плоскостей
"погасят" друг друга и поэтому не изменят
поворотный характер оси 2-го порядка,
параллельной линии пересечения исходных
плоскостей. Однако за счет взаимодействия этой
оси с перпендикулярным к ней вектором обеих плоскостей
"погасят" друг друга и поэтому не изменят
поворотный характер оси 2-го порядка,
параллельной линии пересечения исходных
плоскостей. Однако за счет взаимодействия этой
оси с перпендикулярным к ней вектором 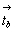 (трансляционной
компонентой плоскости nx) она будет
перенесена на середину этого вектора и окажется
в положении (трансляционной
компонентой плоскости nx) она будет
перенесена на середину этого вектора и окажется
в положении 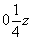 (рис. 76, 4). (рис. 76, 4).
5. Дальнейшее взаимодействие полученной оси 2z
с координатными трансляциями элементарной
ячейки обусловит периодичность этих осей вдоль
координатных направлений 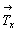 и и 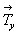 через через 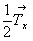 и и 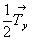 (рис. 76, 5). (рис. 76, 5).
Поскольку все возможные позиции в этой
пространственной группе оказываются занятыми
одинаковыми по характеру осями, в данном случае
нет смысла учитывать последовательность
проводимых симметрических операций (nx .
cy или cy . nx ),
от которой зависит положение результирующей оси,
так как некоммутативность симметрических
операций не сказывается на конечном результате
(см. с. 59).
Таким образом, на этой промежуточной
стадии оказывается построенным график
гемиморфной группы Pnc2 (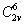 ) 1. ) 1.
6. Далее, нанеся на график плоскость 3-й
позиции - плоскость аz, получим в
качестве результата ее взаимодействия с
вертикальными плоскостями nx и сy
горизонтальные оси симметрии 2-го порядка (рис. 76, 6).
а) nx . az = (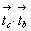 . mx) . (mz
. . mx) . (mz
. 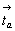 ) --> 21(y). ) --> 21(y).
Операции отражения в двух взаимно
перпендикулярных плоскостях симметрии mx
и mz дадут ось 2y. Вектор 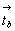 , параллельный
возникшей оси, превратит ее в винтовую 21(y)
, каждый же из векторов , параллельный
возникшей оси, превратит ее в винтовую 21(y)
, каждый же из векторов 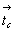 и и 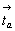 ,
взаимодействуя с полученной осью 21(y),
перенесет ее на свою середину, т.е. на ,
взаимодействуя с полученной осью 21(y),
перенесет ее на свою середину, т.е. на 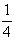 соответствующей
координатной трансляции: вектор соответствующей
координатной трансляции: вектор 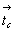 поднимет ось 21(y) на поднимет ось 21(y) на 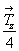 , а вектор , а вектор 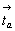 перенесет ее в направлении оси X на
величину перенесет ее в направлении оси X на
величину 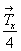 . В результате
будет получена винтовая ось 21(y) в
положении . В результате
будет получена винтовая ось 21(y) в
положении 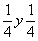 (рис.
76, 6). (рис.
76, 6).
б) cy .az = (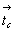 . my) . (mz
. . my) . (mz
. 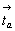 ) --> 21(x). ) --> 21(x).
И вновь операции отражения в двух
плоскостях my и mz дадут ось 2-го
порядка, взаимодействие которой с
трансляционной составляющей 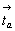 превратит ее в винтовую 21(x),
которая, в свою очередь, взаимодействуя с
вектором превратит ее в винтовую 21(x),
которая, в свою очередь, взаимодействуя с
вектором 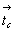 , окажется
передвинутой на , окажется
передвинутой на 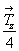 и,
таким образом, будет локализована в положении и,
таким образом, будет локализована в положении 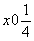 (рис. 76, 6). (рис. 76, 6).
7. Взаимодействие полученных осей 21(x)
и 21(y) с координатными трансляциями
элементарной ячейки 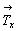 , , 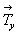 и и 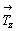 вновь обусловит периодичность этих осей
через вновь обусловит периодичность этих осей
через 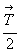 вдоль
координатных направлений (рис. 76, 7).
В результате развернутый символ данной
пространственной группы будет вдоль
координатных направлений (рис. 76, 7).
В результате развернутый символ данной
пространственной группы будет 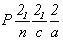 . .
8. Взаимодействие каждой пары
симметрических операций любой позиции символа
(оси 2-го порядка и перпендикулярной к ней
плоскости симметрии) приведет к появлению
инверсии в качестве результирующей
симметрической операции. Если ни плоскость, ни
перпендикулярная к ней ось симметрии не имеют
трансляционных составляющих, то положение
центра инверсии четко фиксируется точкой
пересечения плоскости и оси. В том случае, если
какой-либо из названных элементов симметрии
содержит трансляционную компоненту, то
возникший центр инверсии переместится за счет
взаимодействия с этим вектором на его середину
(см. с. 58).
Так, 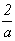 = 2z
. mz . = 2z
. mz . 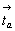 . Центр инверсии, возникший при
взаимодействии 2z . mz ,
переместится вектором . Центр инверсии, возникший при
взаимодействии 2z . mz ,
переместится вектором 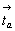 на его середину в позицию на его середину в позицию 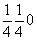 (рис. 76, 8). (рис. 76, 8).
9. Последующее взаимодействие
полученного центра инверсии с координатными
трансляциями обусловит периодичность центров во
всех координатных направлениях через 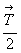 (рис. 76, 9).
Возможность получения одного и того же семейства
центров инверсии в результате взаимодействия
любой пары симметрических операций ( (рис. 76, 9).
Возможность получения одного и того же семейства
центров инверсии в результате взаимодействия
любой пары симметрических операций (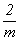 ) на каждой из трех
позиций символа является хорошей проверкой
правильности их (центров инверсии) локализации: ) на каждой из трех
позиций символа является хорошей проверкой
правильности их (центров инверсии) локализации:
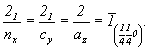
10. Важным компонентом вычерчивания
графиков пространственных групп симметрии
является правильный выбор начала координат.
В соответствии со стандартом, принятым в
Интернациональных таблицах, начало координат
выбирают в самой высокосимметричной и
максимально фиксированной (т.е. самой
неподвижной - с минимальным числом степеней
свободы) точке. При этом число степеней свободы
указывает на количество координатных
направлений, передвигаясь вдоль которых, точка
не меняет своей симметрии.
Качественной оценкой
симметричности той или иной позиции в данной
пространственной группе является ее симметрия -
наличие пересекающихся в этой точке конечных
(макро) элементов симметрии, т.е. ее точечная
группа симметрии. Количественной же мерой
служит так называемая величина симметрии,
характеризующая симметрию данной позиции, т.е.
порядок - размножающая способность - точечной
группы. Например, порядок точечной группы mmm
- 8, m - 2 и т.д.
Если позиции имеют одинаковую
величину симметрии, то предпочтение при выборе
начала координат отдается наиболее неподвижной
из них. Например, центр инверсии 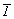 (величина симметрии 2, нет степеней
свободы) предпочтительнее точки с симметрией 2
(величина симметрии 2, одна степень свободы),
далее идет точка на зеркальной плоскости
симметрии m (величина симметрии 2, две степени
свободы) и т.д. (величина симметрии 2, нет степеней
свободы) предпочтительнее точки с симметрией 2
(величина симметрии 2, одна степень свободы),
далее идет точка на зеркальной плоскости
симметрии m (величина симметрии 2, две степени
свободы) и т.д.
В рассматриваемом примере из двух
точек частного положения с симметрией 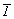 и 2 в качестве начала
координат выбирается четко фиксированная
центром инверсии позиция (без степеней свободы),
после чего график искомой пространственной
группы перерисовывается с новым началом
координат (рис. 76, 10). и 2 в качестве начала
координат выбирается четко фиксированная
центром инверсии позиция (без степеней свободы),
после чего график искомой пространственной
группы перерисовывается с новым началом
координат (рис. 76, 10).
Выбор начала координат в гемиморфных
группах не всегда однозначен, так как
отсутствие центров инверсии заставляет выбрать
для него условную точку на поворотной оси (если
она присутствует), т.е. в позиции с одной степенью
свободы (точку с одной нефиксированной
координатой). При отсутствии поворотных осей 2-го
порядка начало координат выбирается на
плоскости симметрии m (как, например, в пр. гр. Pmc21
(рис. 77, а)): при этом, если
возможно, такую точку обычно выбирают на
винтовой оси 21(z), расположенной в
плоскости mx, или на линии пересечения
плоскостей mx и ny (как в пр. гр. Рmn21
(рис. 77, б)) для облегчения
сопоставления с соответствующей голоэдрической
надгруппой. Однако такое положение выбранной в
качестве начала координат точки не повышает ее
величину симметрии и не уменьшает число степеней
свободы, т.е. она остается эквивалентной любой
другой точке, расположенной на плоскости m
(точка 1 на рис. 78). Если точка
расположена на трансляционном элементе
симметрии (плоскости скользящего отражения или
на винтовой оси) (точка 2 на рис. 78),
то она ведет себя так же, как точка общего
положения (точка 3), т.е. размножается этим
элементом симметрии и не фиксируется им, тогда
как точка (1), расположенная на
макроэлементе симметрии, - точка частного
положения - зафиксирована и им не размножается (рис. 78).
При отсутствии в какой-либо
пространственной группе точек частного
положения (точек с величиной симмет-рии большей 1)
начало координат выбирают на винтовых осях 21
, напри-мер как в пр. гр. Pca21 (см. рис. 77, в) и Pna21 .
Следуя выше сформулированным правилам
выбора начала координат, нетрудно понять, почему
в голоэд-рической группе Pmmn предпочтение
отдано не центру инверсии (с величиной симметрии,
равной 2), а моно-вариантному (см. с. 234) комплексу mm2
(с большей величиной симметрии, равной 4) в точке
на уровне центров инверсии. Во всех остальных
случаях центросимметричный комплекс 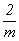 (с величиной симметрии,
равной 4) предпочтен ацентричному комплексу 222
с той же величиной симметрии. (с величиной симметрии,
равной 4) предпочтен ацентричному комплексу 222
с той же величиной симметрии.
Определенные затруднения вызывает
построение графиков пространственных групп,
элементы симметрии которых содержат
трансляционные компоненты, равные 1/4
координатных трансляций пространственной
решетки, т.е. графиков пространственных групп с
клиноплоскостями d - гемиморфной (Fdd2) и
голоэдрической (Fddd) (см. с. 63 - 68).
Некоммутативность взаимодействий составляющих
эти плоскости симметрических операций
заставляет учитывать последовательность их
выполнения, так как от этого зависит
возникновение либо осей 2, либо осей 21,
чередующихся вдоль координатных направлений
элементарной ячейки в одной и той же
пространственной группе.
Таким образом, присутствие только двух
взаимно перпендикулярных клиноплоскостей d
обусловливает чередование осей 2 (21)
через 1/4 координатных трансляций элементарной
ячейки. А это однозначно указывает на
гранецентрированный тип решетки Браве и на
единственно возможную группу ромбической
гемиэдрии с такими плоскостями - Fdd2.
Действительно, дважды повторенное отражение в
одной из плоскостей d сведется к сумме ее
трансляционных компонент: (dx)2 = (mx)2
. (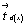 )2,
так как дважды проведенная операция отражения в
плоскости mx равносильна операции
идентичности, а сумма трансляционных компонент )2,
так как дважды проведенная операция отражения в
плоскости mx равносильна операции
идентичности, а сумма трансляционных компонент 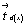 обусловит
возникновение истинной трансляции, центрирующей
грань А элементарной ячейки. Таким же путем
устанавливают и центрировку грани В, а
следовательно, и третью - производную
трансляцию ( обусловит
возникновение истинной трансляции, центрирующей
грань А элементарной ячейки. Таким же путем
устанавливают и центрировку грани В, а
следовательно, и третью - производную
трансляцию (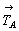 + +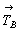 = = 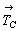 ), центрирующую грань С. ), центрирующую грань С.
Аналогичные рассуждения приведут и к
единственно возможной группе ромбической
голоэдрии с d плоскостями - Fddd, построение
графика которой по описанному на с. 109- 112 плану
не должно вызывать затруднений.
Позиции осей 2 и 21 в пр. гр.
Fdd2 и Fddd (см. рис. 40) можно выявить и из
геометрического анализа проекций
пространственных групп, где указанные оси
локализованы в центрах разных прямоугольников,
оконтуренных плоскостями d: стрелки
клиноплоскостей вокруг поворотной оси 2
направлены навстречу друг другу (или в
противоположные стороны), вокруг же винтовой оси 21
- по часовой стрелке (или против), т.е. в одну
сторону:
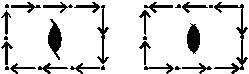 . .
Обратим еще раз внимание на тот факт,
что при вычерчивании графиков пространственных
групп с плоскостями d необходимо учитывать не
только взаимодействие симметрических операций,
входящих в состав клиноплоскостей, но и их
непосредственное действие друг на друга, а также
последовательность выполняемых операций
симметрии. В итоге окажется, что исходная
плоскость d любой позиции символа (d = m .
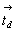 ) c трансляционным
вектором, направленным вдоль одной диагонали
грани элементарной ячейки, будет неизбежно
сопровождаться параллельной и отстоящей от
исходной на ) c трансляционным
вектором, направленным вдоль одной диагонали
грани элементарной ячейки, будет неизбежно
сопровождаться параллельной и отстоящей от
исходной на 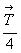 другой
клиноплоскостью d' = m . другой
клиноплоскостью d' = m . 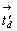 со скольжением вдоль другой диагонали
грани ячейки (см. с. 63). Таким образом, развернутая
запись голоэдрической группы Fddd будет со скольжением вдоль другой диагонали
грани ячейки (см. с. 63). Таким образом, развернутая
запись голоэдрической группы Fddd будет 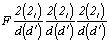 . .
Выбор начала координат в гемиморфной
пространственной группе Fdd2 очевиден - на
поворотной оси 2-го порядка (в точке с одной
степенью свободы) (см. рис. 40), в
голоэдрической пр. гр. Fddd - в точке
максимальной симметрии 222.
При вычерчивании графиков
пространственных групп ромбической осевой
гемиэдрии, т.е. групп класса 222, наибольшие
затруднения возникают при локализации осей 2-го
порядка. Однако, воспользовавшись основным
положением Ю.В.Вульфа о том, что каждая ось
является произведением двух плоскостей
симметрии, присутствующих в голоэдрических
группах, но исчезающих в младших, подчиненных
точечному классу 222, легко установить
характер и позицию результирующих осей. Для
этого поворот вокруг каждой оси 2-го порядка
следует представить отражениями в двух взаимно
перпендикулярных плоскостях симметрии и
рассмотреть их взаимодействие.
Возможны 6 вариантов взаимодействий
пересекающихся или скрещивающихся исходных
осей: 2 .2, 21 .21 и 2 .
21 . Рассмотрим результат взаимодействия
двух пересекающихся под углом 90o поворотных осей
2-го порядка (2x и 2y): ни
характер, ни положение результирующей
поворотной оси 2z не вызывает сомнений
даже без дополнительных построений (рис.
79, 1). Действительно, заменив поворот вокруг оси 2x
отражениями в плоскостях my и mz,
а поворот вокруг оси 2y - отражениями в
плоскостях mx и my , увидим, что
два последовательных отражения в одной и той же
плоскости дадут операцию идентичности,
взаимодействие же оставшихся операций my
и mx обусловит появление поворотной оси
2-го порядка, совпадающей с линией пересечения
плоскостей:
2(x00) . 2(0y0)
= my . [mz .mz]
. mx = 2(00z).
В результате получим график
пространственной группы Р222, в которой каждая
из поворотных осей указывает на то, что две
другие пересекаются.
Если порождающими являются две
пересекающиеся винтовые оси 2-го порядка, то
взаимодействие плоскостей симметрии, их
заменяющих: 21(x) = аy . mz
, 21(y) = mz . bx,
из-за отсутствия в плоскостях аy = mу
.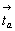 и bx = mx
. и bx = mx
. 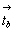 трансляционных векторов, параллельных
координатной оси Z, приведет к возникновению
поворотной оси 2, которая при взаимодействии
с перпендикулярными к ней векторами
трансляционных векторов, параллельных
координатной оси Z, приведет к возникновению
поворотной оси 2, которая при взаимодействии
с перпендикулярными к ней векторами 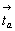 и и 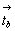 окажется в положении окажется в положении 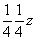 (рис. 79, 2): (рис. 79, 2):
21(x00) . 21(0y0)
= ay . [mz . mz] .
bx = 2(1/4 1/4 z).
В результате получим график
пространственной группы P21212, где
поворотная ось 3-й позиции указывает на то, что
исходные оси 21(x) и 21(y)
пересекаются, а каждая из осей 21
свидетельствует о том, что две другие оси
скрещиваются.
В случае пересечения разнородных осей
2-го порядка
2(x00) . 21(0y0)
= my . [mz . mz ] .
by = 2(0 1/4 z) (рис.
79, 3)
опять получим поворотную ось 2z,
но уже в позиции 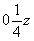 (2z
. (2z
. 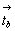 ). В
стандартной записи полученной таким образом
пространственной группы P2212 = Р2221
на 3-й позиции расположена ось, отличающаяся по
характеру от первых двух. ). В
стандартной записи полученной таким образом
пространственной группы P2212 = Р2221
на 3-й позиции расположена ось, отличающаяся по
характеру от первых двух.
Далее, проанализировав оставшиеся три
варианта взаимодействия скрещивающихся осей 2-го
порядка, увидим (рис. 79, 4- 6), что
результатом всех перечисленных вариантов
взаимодействий будет винтовая ось 21 ,
положение которой зависит от горизонтальных
трансляционных составляющих плоскостей
симметрии:
2(x00) . 2(0y 1/4)
= my . [mz . mz ] .
cx = 21(00z),
21(x00) . 21(0y 1/4)
= ay . [mz . mz ]
. nx = 21(1/4 1/4 z),
2(x00) . 21(0y 1/4)
= my . [mz . mz ] .
nx = 21(0 1/4 z).
Из трех полученных сочетаний осей 2-го
порядка - 2221, 212121, 221
21 = 21 21 2 - лишь одно будет
составлять новую пространственную группу P21 21
21, являющуюся подгруппой двух
голоэдрических: Pbca и Pnma.
Обратим еще раз внимание на полезное
правило, облегчающее представление осевых
пространственных групп: если порожденная ось
поворотная, то порождающие оси независимо от их
характера пересекаются, если же порожденная ось
винтовая, то
порождающие оси скрещиваются.
Построение графиков пространственных
групп осевой гемиэдрии с Р-решеткой
завершается нанесением остальных осей 2-го
порядка, повторяющихся с периодичностью в
половину координатных трансляций (см. с. 54).
Начало координат во всех четырех вычерченных
графиках пространственных групп ромбической
осевой гемиэдрии выбирается в соответствии с
общепринятым стандартом: на поворотных осях 2-го
порядка. И лишь в пространственной группе Р212121
, не имеющей зафиксированных элементами
симметрии точек частного положения, условно
начало координат выбирают в точке,
равноудаленной от всех трех скрещивающихся осей 21
, т.е. так же, как в голоэдрических
надгруппах этой группы - Pnma и Pbca, где,
однако, эта позиция совпадает с центром инверсии
(рис. 80).
Графическое представление
непримитивных пространственных групп осевой
гемиэдрии не вызывает затруднений, ибо каждый
раз вычерчивание начинается с нанесения
элементов симметрии, обозначенных в
"подрешеточном" символе группы и лишь затем
вводятся дополнительные трансляционные векторы
той или иной решетки, обусловливающие
соответствующие чередования осей. Например,
исходный комплекс подрешеточных элементов
симметрии в пространственных группах I222 и I212121
(рис. 81, а, б) указывает на то,
что в первой группе однородные оси симметрии
пересекаются, во второй - скрещиваются. Введение
центрирующего объем вектора 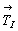 обусловливает чередование осей 2(21)
на всех позициях символа обеих групп. Однако при
этом сформулированные выше особенности
расположения осей сохраняются, что и отражено в
стандартной (условной) записи этих
пространственных групп симметрии. обусловливает чередование осей 2(21)
на всех позициях символа обеих групп. Однако при
этом сформулированные выше особенности
расположения осей сохраняются, что и отражено в
стандартной (условной) записи этих
пространственных групп симметрии.
| 
